LeetCode刷题心得
LeetCode刷题笔记
- 滑动窗口&双指针
- 3 无重复字符的最长子串
- 11. 盛最多水的容器
- 15. 三数之和
- 76 最小覆盖子串
- 438 找到字符串中所有字母异位词
- 动态规划
- 10 正则表达式匹配
- 44 通配符匹配
- 122 买卖股票的最佳时机 II
- 494 目标和i
- 排序
- 215 数组中的第K个元素★★★
- 347 前k个高频元素
- LRU
- 栈遍历树
- 前序
- 中序
- 后序
- 位运算符 ★★★
- 191 位1的个数
- 338 比特位计算
- 连续子串的和
- 437 路径总和III
- 560 和为K的子数组
- 利用当前数组记录信息
- 41 缺失的第一个正数
- 链表深拷贝
- 138 复制带随机指针的链表
- cmp函数的巧妙使用,判断a+b>b+a
- 179 最大数
- 判断素数
- 杂项
- 5 最长回文子串
- 19 删除链表的第n个节点
- 20 有效的括号
- 22 括号生成
- 31 下一个排列
- 32 最长有效括号
- 130 被围绕的区域
- 189 旋转数组
- 448 找到所有数组中消失的数字
- 581 最短无序连续子数组
- 621 任务调度器
- 739 每日温度
- 面试题:寻找最大差
本笔记按照解题方法的不同进行分类
滑动窗口&双指针
3 无重复字符的最长子串
给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
示例:
输入: “abcabcbb”
输出: 3
解释: 因为无重复字符的最长子串是 “abc”,所以其长度为 3。
==============================================================================
滑动窗口设有左指针和右指针,并按照不同的规则移动左右两个指针。
本题记录中间的数据有三种方法:
1.使用map进行存储,key为char,value为int,记录出现重复元素上一次出现的位置。
2.使用set进行存储,当出现相同元素时依次删除左边的元素,只到将相同元素删掉位置,也可以达到将左指针送到不包含重复元素的位置。
unordered_set<char> lookup;
while (lookup.find(s[i]) != lookup.end()){
lookup.erase(s[left]);
left ++;
}
3.针对全是char类型的情况可使用数组进行优化:
int [26] :用于字母 ‘a’ - ‘z’ 或 ‘A’ - ‘Z’
int [128] :用于ASCII码
int [256] :用于扩展ASCII码
第三种方法的优势很明显,速度快且节省内存
11. 盛最多水的容器
给定 n 个非负整数 a1,a2,…,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器,且 n 的值至少为 2。
示例:
输入: [1,8,6,2,5,4,8,3,7]
输出: 49
实现也是滑动窗口的一种,双指针法,一个left,一个right,当left的数字比right小或者等的时候,增加left,反之减少right,并且每动一次就记录值和最大值比较,一轮过后即可实现找到最大面积。
这个窗口是不断缩小的。
15. 三数之和
给定一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?找出所有满足条件且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例:
给定数组 nums = [-1, 0, 1, 2, -1, -4],
满足要求的三元组集合为:
[
[-1, 0, 1],
[-1, -1, 2]
]
给定一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?找出所有满足条件且不重复的三元组。
注意:答案中不可以包含重复的三元组。
所有跟数字有关的题,可以先考虑一下排序以后按照顺序进行搜索
本题的思路也是如此,再排序后,先确定一个数字,然后针对剩下的数字以双指针的形式进行搜索,如果小了则left左移,大了right右移。需要注意的问题是,不能选用中间的数字作为第一个数字,不然再去重的时候会漏掉一些组合。选择左边或者右边的数字作为第一个数字,然后搜索剩下两个。
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
Arrays.sort(nums);
List<List<Integer>> res = new ArrayList();
for (int i = 0; i < nums.length - 2 && nums[i] <= 0; ++i){
if(i != 0 && nums[i] == nums[i - 1]) continue;
int l = i + 1, r = nums.length - 1;
while(l < r){
//这个条件的意思是:left等于第一个数 或者 left不为第一个数且不等于前一个数
//且 r等于第一个数 或者 r不为第一个数且不等于后一个数
//保证去重,不要漏掉等于第一个数的形式
if ((l == i + 1 || (l > i + 1 && nums[l] != nums[l - 1])) &&
(r == nums.length - 1 || (r < nums.length - 1 && nums[r] != nums[r + 1]))){
if (nums[l] + nums[r] + nums[i] == 0){
res.add(Arrays.asList(nums[i], nums[l], nums[r]));
}
}
if (nums[l] + nums[r] + nums[i] >= 0){
r--;
} else {
l++;
}
}
}
return res;
}
}
76 最小覆盖子串
采用滑动窗口的做法,如果没有满足所有的覆盖,移动右指针,然后移动左指针进行精简,找到在当前右指针下的最小覆盖字串。
要注意:
1、map中只能存放包装类,不能存放基本类型
2、Integer超过127的缓存池范围以后,使用==判断的就是两个引用的地址,要使用equals方法或者使用intValue()转换
3、map查值可以使用getOrDefault方法,直接设置初值为0;
4、优化方法:使用一个map记录下所有的s中有t的位置坐标,然后直接在这个小的只包含t中字符的字符串中进行扫描。
public String minWindow(String s, String t) {
int needCnt = 0, hasCnt = 0;
String res = "";
HashMap<Character, Integer> need = new HashMap<>();
HashMap<Character, Integer> has = new HashMap<>();
for (int i = 0; i < t.length(); ++i){
int temp = need.getOrDefault(t.charAt((i)), 0);
need.put(t.charAt(i), temp + 1);
}
needCnt = need.size();
int left = 0, right = 0;
int[] record = new int[]{-1, 0, 0};
while (right < s.length()){
char sr = s.charAt(right);
if (need.containsKey(sr)){
int temp = has.getOrDefault(sr, 0);
has.put(sr, temp + 1);
if (has.get(sr).intValue() == (need.get(sr).intValue())){
hasCnt++;
}
}
while (hasCnt == needCnt){
if (record[0] == -1 || right - left + 1 < record[0]){
record[0] = right - left + 1;
record[1] = left;
record[2] = right;
}
char sl = s.charAt(left);
if (need.containsKey(sl)){
has.put(sl, has.get(sl) - 1);
if (has.get(sl).intValue() < need.get(sl).intValue()){
hasCnt--;
}
}
left++;
}
right++;
}
return record[0] == -1 ? "" : s.substring(record[1], record[2] + 1);
}
438 找到字符串中所有字母异位词
给定一个字符串 s 和一个非空字符串 p,找到 s 中所有是 p 的字母异位词的子串,返回这些子串的起始索引。
字符串只包含小写英文字母,并且字符串 s 和 p 的长度都不超过 20100。
说明:
字母异位词指字母相同,但排列不同的字符串。
不考虑答案输出的顺序。
示例 1:
输入:
s: “cbaebabacd” p: “abc”
输出:
[0, 6]
解释:
起始索引等于 0 的子串是 “cba”, 它是 “abc” 的字母异位词。
起始索引等于 6 的子串是 “bac”, 它是 “abc” 的字母异位词。
示例 2:
输入:
s: “abab” p: “ab”
输出:
[0, 1, 2]
解释:
起始索引等于 0 的子串是 “ab”, 它是 “ab” 的字母异位词。
起始索引等于 1 的子串是 “ba”, 它是 “ab” 的字母异位词。
起始索引等于 2 的子串是 “ab”, 它是 “ab” 的字母异位词。
本题目思路和上面一样,只是更改判断处的代码即可。维护一个list存放结果。
当right- left + 1 == p.length()且hasCnt 等于needCnt的时候,即可以保证在这个字串中所有的字符串都是和p中一一对应的,有额外的字符或者某个字符多了那么他的length一定会超出p的范围(在保证所有类别字符都满足的情况下)
动态规划
10 正则表达式匹配
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 ‘.’ 和 ‘’ 的正则表达式匹配。
‘.’ 匹配任意单个字符
'’ 匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串。
说明:
s 可能为空,且只包含从 a-z 的小写字母。
p 可能为空,且只包含从 a-z 的小写字母,以及字符 . 和 *。
示例 1:
输入:
s = “aa”
p = “a”
输出: false
解释: “a” 无法匹配 “aa” 整个字符串。
示例 2:
输入:
s = “aa”
p = “a*”
输出: true
解释: 因为 ‘*’ 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 ‘a’。因此,字符串 “aa” 可被视为 ‘a’ 重复了一次。
**==============================================================================**
典型的动态规划题目,目前我知道的动态规划的题目主要有三种形式。
第一:正常的dp数组,找到递推表达式,进行动态规划
第二:递归,递归是一种自上而下的推衍方式,不过需要优化的是记录一个memo数组,在查询到有记录的情况下就直接跳过递归。
第三:迭代,迭代是一种自下而上的方式,好处是可以一遍记录一遍往上推衍,本身后面的步骤就是在前面的基础上完成的,因此之前的记录也保存了下来。
我认为后面两种本身就也有动态规划的影子在,符合最小单元块的概念,重要的是要找到递推公式即可。
class Solution {
public boolean isMatch(String s, String p) {
boolean dp[][] = new boolean[s.length() + 1][p.length() + 1];
//dp[i][j]表示s的前i位和p的前j位是否匹配
dp[0][0] = true;
//处理p的前几位有*且使*之前的字符取零个的情况
for(int j = 0; j < p.length(); ++j){
if(p.charAt(j) == '*' && dp[0][j - 1]) {//这里代表的是把*前面的那一位字符去掉,所以未j-1
dp[0][j + 1] = true;
}
}
for(int i = 0; i < s.length(); ++i){
for(int j = 0; j < p.length(); ++j){
if(p.charAt(j) == '.' || p.charAt(j) == s.charAt(i)){
dp[i + 1][j + 1] = dp[i][j];
}
if (p.charAt(j) == '*'){
if (p.charAt(j - 1) != s.charAt(i) && p.charAt(j - 1) != '.'){
dp[i + 1][j + 1] = dp[i + 1][j - 1];//取零
} else {
//分别为前位字符取2(a*表示aa),前位字符取1(a*表示a),前位字符取0的情况(a*表示没有)
dp[i + 1][j + 1] = (dp[i + 1][j] || dp[i][j + 1] || dp[i + 1][j - 1]);
}
}
}
}
return dp[s.length()][p.length()];
}
}
44 通配符匹配
给定一个字符串 (s) 和一个字符模式 § ,实现一个支持 ‘?’ 和 ‘’ 的通配符匹配。
‘?’ 可以匹配任何单个字符。
'’ 可以匹配任意字符串(包括空字符串)。
两个字符串完全匹配才算匹配成功。
说明:
s 可能为空,且只包含从 a-z 的小写字母。
p 可能为空,且只包含从 a-z 的小写字母,以及字符 ? 和 *。
输入:
s = “adceb”
p = “ab”
输出: true
dpij代表的是s中第i个字符和p中第j个字符是否匹配
本题和10的思路大致相似,但是要注意两点:
1、初始化边界值:当dp0i的初始化值,当p的开头为一串*的时候为true,否则为false
2、状态转移方程,当p中的字符为×的时候,dp j i = dp j-1 i || dp j i-1
其中:dp j i - 1好理解,即为 当前×取空, dp j - 1 i 比较难理解,这和×的定义有关,他可以代表任意个字符,如果 j-1 和 i匹配成功,那么这个×可以多匹配一个。这个推导公式的前提在于之前j i-1已经赋值过了。
e.g. s:abcd p:ab×
ab和ab可以匹配,那么ab和ab×就可以匹配(×取0) dp j i - 1
ab和ab×可以匹配,那么abc、abcd就可以和ab×匹配(x多取几个字符)dp j - 1 i
public boolean isMatch(String s, String p) {
int lens = s.length(), lenp = p.length();
boolean[][] dp = new boolean[lens + 1][lenp + 1];
dp[0][0] = true;
if (lenp != 0 && p.charAt(0) == '*'){
int t = 0;
while (t < lenp && p.charAt(t) == '*'){
dp[0][t + 1] = true;
t++;
}
}
for (int i = 1; i <= lenp; ++i){
char cp = p.charAt(i - 1);
for (int j = 1; j <= lens; ++j){
char cs = s.charAt(j - 1);
if (cs == cp || cp == '?'){
dp[j][i] = dp[j - 1][i - 1];
} else if (cp == '*'){
dp[j][i] = dp[j - 1][i] || dp[j][i - 1];
}
//System.out.print(1);
}
}
return dp[lens][lenp];
}
122 买卖股票的最佳时机 II
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
一般来讲,能用贪心算法解决的问题,也都可以用动态规划解决。
首先最想想到的方法是寻找波峰峰谷,利用每一个波峰减去波谷即可,但是用依次扫描判断是否比左右值大/小的方式太过繁琐,需要判断许多额外条件。比较方便的找到波峰以后向后推移找到波谷,找到波谷以后向后推找到波峰。
其次是贪心算法,这道题由于没有限制股票买入卖出的冷却时间,那么每一天都进行买入卖出都是被允许的。即每一天的收益=当天的价格-前一天的价格,我们只需要统计为正数的价格即可。
public int maxProfit(int[] prices) {
int total = 0;
for (int i = 1; i < prices.length; ++i){
if (prices[i] > prices[i - 1]){
total += prices[i] - prices[i - 1];
}
}
return total;
}
最后是动态规划,动态规划需要两个状态变量:即当天是持有现金还是持有股票。
持有现金的话可以选择维持前一天持有现金的状态 或者 卖出当前的股票。取两者最大值
持有股票的话可以选择前一天持有股票的状态 或者 买入当前的股票。取两者最大值。
最后返回最后一天持有现金的状态即可。
int[][] dp = new int[len][2];
//0表示持有现金,1表示持有股票
dp[0][0] = 0;
dp[0][1] = -prices[0];
for (int i = 1; i < len; i++) {
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
}
return dp[len - 1][0];
//可以简化变量,直接只用两个状态变量即可。
int cash = 0;
int hold = -prices[0];
int preCash = cash;
int preHold = hold;
for (int i = 1; i < len; i++) {
cash = Math.max(preCash, preHold + prices[i]);
hold = Math.max(preHold, preCash - prices[i]);
preCash = cash;
preHold = hold;
}
return cash;
494 目标和i
给定一个非负整数数组,a1, a2, …, an, 和一个目标数,S。现在你有两个符号 + 和 -。对于数组中的任意一个整数,你都可以从 + 或 -中选择一个符号添加在前面。
返回可以使最终数组和为目标数 S 的所有添加符号的方法数。
示例 1:
输入: nums: [1, 1, 1, 1, 1], S: 3
输出: 5
解释:
-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3
一共有5种方法让最终目标和为3。
回溯法很简单直接递归就完事了。
动态规划:
dp[i][j] 表示的是前i项和为j的结果的个数
因此dp[i][j] = dp[i - 1][j - nums[i]] + dp[i - 1][j + nums[i]]
分别是第i项取加号和第i项取减号的结果
public int findTargetSumWays(int[] nums, int S) {
//dp[i][j] 表示的是前i项和为j的结果的个数
//因此dp[i][j] = dp[i - 1][j - nums[i]] + dp[i - 1][j + nums[i]]
//分别是第i项取加号和第i项取减号的结果
if (S > 1000 || S < -1000) return 0;
int[][] dp = new int[nums.length][2001];
dp[0][nums[0] + 1000]++;
dp[0][1000 - nums[0]]++;
for (int i = 1; i < nums.length; ++i){
for (int j = 0; j < 2001; ++j){
if (j - nums[i] >= 0 && j - nums[i] < 2001){
dp[i][j] += dp[i - 1][j - nums[i]];
}
if (j + nums[i] >= 0 && j + nums[i] < 2001){
dp[i][j] += dp[i - 1][j + nums[i]];
}
}
}
return dp[nums.length - 1][S + 1000];
}
0-1背包:

dp[i]中存放的是和为i的方案的个数。
因此dp[i]=dp[i]+dp[i - num];
不放入当前数字和放入当前数字。
public int findTargetSumWays(int[] nums, int S) {
long sum = 0;//防止值超出
for (int num : nums) sum += num;
if ((S + sum) % 2 == 1 || S > sum) return 0;
S = (S + sum) / 2; // 要选出来的正数的和
int[] dp = new int[S + 1];
//dp[i]中存放的是总和为i的方案个数
dp[0] = 1;
for (int num : nums){
for (int j = S; j >= num; --j){
dp[j] += dp[j - num];
}
}
return dp[S];
}
排序
215 数组中的第K个元素★★★
先排序,后找到第k大的元素
1、堆排序,使用priority即可
2、普通快排:
public static int findKthLargest(int[] nums, int k) {
return divide(nums, 0, nums.length - 1, nums.length - k);
}
public static int divide(int[] nums, int low, int high, int k){
int index = findIndex(nums, low, high);
if (index == k - 1)return nums[index];
else if (index < k - 1){
return divide(nums, index + 1, high, k);
} else {
return divide(nums, low, index - 1, k);
}
}
public static int findIndex(int[] nums, int low, int high){
int current = nums[low];
while (low < high){
while (low < high && nums[high] >= current) high--;
nums[low] = nums[high];
while (low < high && nums[low] <= current) low++;
nums[high] = nums[low];
}
nums[low] = current;
return low;
}
//速度为17ms,击败29%,速度还是比较慢的
public int findIndex(int[] nums, int low, int high){
//写法2,按照下面那种写法
//不填开头的swap是29ms,加了以后是2ms
swap(nums, low, low + (high - low) / 2);
int j= high;
for (int i = high; i > low; --i){
if (nums[i] > nums[low]){
swap(nums, i, j--);
}
}
swap(nums, low, j);
return j;
}
3、分治随机收缩,增强了随机性?直接筛选出前k个元素,速度比正常快排快很多,据说时间复杂度是o(n)
public int divid(int[] nums, int l, int r, int k){
//随机选取一个数作为标志,换到最后面去
swap(nums, r, l + (r - l) / 2);
//y表示的是比最后的标志位大的数的个数
int y = l;
//x表示的是依次遍历前面的所有元素和最后一位进行比较,把比最后一位大的数都换到前面去
for(int x = l; x < r; ++x){
if(nums[x] > nums[r]){
//如果当前位比最后一位大,那么把这一位换到最前面去,并把y加一
swap(nums, y++, x);
}
}
//把最后一位换到y的位置上去
swap(nums, r, y);
if(y + 1 == k)return nums[y];
if(y + 1 < k)return divid(nums, y + 1, r, k);
return divid(nums, l, y, k);
}
public int findKthLargest(int[] nums, int k) {
return divid(nums, 0, nums.length - 1, k);
}
public void swap(int[] nums, int i, int j){
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
//速度快很多,仅1ms
后面分析发现,快的原因就在于找到的这个标志位是随机的,即swap(nums, r, l + (r - l) / 2);这一步。
后面证明就是第二种写法添加一个更换之后速度也非常快(1ms),可能是快排的缺陷
347 前k个高频元素
使用priorityqueue优先队列来维护,优先队列中根据定义不同,维护的是最大堆或者最小堆(只保证最上面的数是最大的或者最小的),每次add或remove的时候会进行更新。
定位方法为
HashMap<Integer, Integer> map = new HashMap<>();
PriorityQueue<Integer> pq = new PriorityQueue<>(new Comparator<Integer>(){
@Override
public int compare(Integer a, Integer b){
return map.get(b) - map.get(a);//b在前是降序,大顶堆
}
});
//或者:
PriorityQueue<Integer> heap =
new PriorityQueue<Integer>((n1, n2) -> map.get(n1) - mapp.get(n2));//升序
for (Integer key : map.keySet()){
//遍历map
pq.add(key);
}
List<Integer> res = new ArrayList<>();
int i = 0;
while (i++ < k){
//每次删除后都会更新,最上面的数一定是最大的
res.add(pq.remove());
}
return res;
LRU
使用linkedlist加hashmap实现,非线程安全,可以将hashmap换为courrenthashmap
class LRUCache {
class DlinkedNode{
int key;
int value;
DlinkedNode prev;
DlinkedNode next;
}
private void addNode(DlinkedNode node){
node.prev = head;
node.next = head.next;
head.next.prev = node;
head.next = node;
}
private void removeNode(DlinkedNode node){
//双向链表同时有四条实现,要同时定义出来进行更改
DlinkedNode prev = node.prev;
DlinkedNode next = node.next;
prev.next = next;
next.prev = prev;
node.prev = node.next = null;
}
//这一步开始的时候这个节点内部就存放的有node信息,因此可以先删掉这个节点,然后在更改
private void moveToHead(DlinkedNode node){
removeNode(node);
addNode(node);
}
private DlinkedNode popTail(){
DlinkedNode res = tail.prev;
removeNode(res);
return res;
}
private HashMap<Integer, DlinkedNode> cache =
new HashMap<Integer, DlinkedNode>();
private int size;
private int capacity;
private DlinkedNode head, tail;
public LRUCache(int capacity) {
this.size = 0;
this.capacity = capacity;
head = new DlinkedNode();
tail = new DlinkedNode();
head.next = tail;
tail.prev = head;
}
//获取节点,如果没有返回-1,如果有返回值且将这个节点放在最前面
public int get(int key) {
DlinkedNode node = cache.get(key);
if (node == null) return -1;
moveToHead(node);
return node.value;
}
//放入节点,如果有则更新值且放在最前面,如果没有则放入且放在最前面,如果超过capacity,则将队尾元素删除
public void put(int key, int value) {
DlinkedNode node = cache.get(key);
if (node == null){
DlinkedNode newNode = new DlinkedNode();
newNode.key = key;
newNode.value = value;
cache.put(key, newNode);
addNode(newNode);
size++;
if (size > capacity){
DlinkedNode tail = popTail();
cache.remove(tail.key);
--size;
}
} else {
node.value = value;
moveToHead(node);
}
}
}
栈遍历树
前序
最简单,直接先放入列表,然后先压左树再压右树就可以了
public static void preOrderIteration(TreeNode head) {
List<Integer> list = new ArrayList<>();
Stack<TreeNode> stack = new Stack<>();
stack.push(head);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
list.add(node.value);
if (node.right != null) {
stack.push(node.right);
}
if (node.left != null) {
stack.push(node.left);
}
}
}
中序
需要一个cur记录当前节点的位置,然后一直压入左子树,然后再进行返回处理
public List < Integer > inorderTraversal(TreeNode root) {
List < Integer > res = new ArrayList < > ();
Stack < TreeNode > stack = new Stack < > ();
TreeNode curr = root;
while (curr != null || !stack.isEmpty()) {
while (curr != null) {
stack.push(curr);
curr = curr.left;
}
curr = stack.pop();
res.add(curr.val);
curr = curr.right;
}
return res;
}
后序
和前序类似,不过这里先放进去的是左子树
前序遍历的过程 是 中左右。
将其转化成 中右左。也就是压栈的过程中优先压入左子树,在压入右子树。
public static void postOrderIteration(TreeNode head) {
if (head == null) {
return;
}
Stack<TreeNode> stack = new Stack<>();
List<Interger> list = new ArrayList<>();
stack.push(head);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
list.add(node.value);
if (node.left != null) {
stack1.push(node.left);
}
if (node.right != null) {
stack1.push(node.right);
}
}
Collections.reverse(lists);
}
位运算符 ★★★
给定 x, k ,求满足 x + y = x | y 的第 k 小的正整数 y 。 | 是二进制的或(or)运算,例如 3 | 5 = 7。
比如当 x=5,k=1时返回 2,因为5+1=6 不等于 5|1=5,而 5+2=7 等于 5 | 2 = 7。
例:
输入:5 1
输出:2
x = 10010010011
y = 00000000(0)00 k = 0
y = 00000000(1)00 k = 1
y = 0000000(1)(0)00 k = 2
y = 0000000(1)(1)00 k = 3
y = 00000(1)0(0)(0)00 k = 4
y = 00000(1)0(0)(1)00 k = 5
…
注意观察括号里的数,为x取0的比特位,而如果把括号里的数连起来看,正好等于k。
得出结论,把k表示成二进制数,填入x取0的比特位,x取1的比特位保持为0,得到y。
循环的思想是每次取得k的最低一位,填入到低位开始,x中比特位为0的位置上。
所以用while来判断k是否大于0,若是,说明k还未完全填完
循环体内,需要找到x当前可以填的位置,我们用bitNum来从右往左扫描x的每一位
public class Zhenti4 {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt(), k = scan.nextInt();
long bitNum = 1;//从低位开始寻找n的二进制中为0的位数
long res = 0;//返回值
while(k != 0)
{
if((n & bitNum) == 0)//从低位开始寻找 &为0表示的就是这一位两者不一样
{
res += (bitNum * (k & 1));//每次取k的最低位加上去
k >>= 1;
}
bitNum <<= 1;
}
System.out.println(res);
}
}
191 位1的个数
编写一个函数,输入是一个无符号整数,返回其二进制表达式中数字位数为 ‘1’ 的个数(也被称为汉明重量)。
示例 1:
输入:00000000000000000000000000001011
输出:3
解释:输入的二进制串 00000000000000000000000000001011 中,共有三位为 ‘1’。
三种写法:
1、使用最低标志位不断&操作,知道为0为止
这里要注意,这里转移位操作应该用>>>而不是>>。>>>不论是正数还是负数高位都补0,而>>正数高位补0,负数高位补1
2、利用掩码,mask=1然后不断的左移掩码,即一位一位的判断即可。
3、利用n&(n-1)的特性,会将n的最后一位1变成0,那么一直变到n==0即可
public int hammingWeight(int n) {
int sum = 0;
while (n != 0) {
sum++;
n &= (n - 1);
}
return sum;
}
338 比特位计算
动态规划加上位运算,重要的是如果找出状态转移方程
方法一:最高标志位,比如说111就是由011加1得来的,那么怎么得来呢
111 = 011 + 100(4) 1011 = 011 + 1000(8) 即,后面加得数是大于前面的2的x次方
或者用 i 做循环验证 b 也可以
public int[] countBits(int num) {
int[] ans = new int[num + 1];
int i = 0, b = 1;
while (b <= num) {
while(i < b && i + b <= num){
ans[i + b] = ans[i] + 1;
++i;
}
i = 0; // reset i
b <<= 1;
}
return ans;
}
方法二:最低标志位,比如说111是由110加最低位的来的,1100是由110加最低位的来的,这个相比于前面的就简单很多
public int[] countBits(int num) {
int[] ans = new int[num + 1];
for (int i = 1; i <= num; ++i)
ans[i] = ans[i >> 1] + (i & 1);
return ans;
}
方法三:最后一个标志位,比如说1110 是由 1100 加1得来得
x&(x-1) 的作用就是去掉最后一个1
public int[] countBits(int num) {
int[] ans = new int[num + 1];
for (int i = 1; i <= num; ++i)
ans[i] = ans[i & (i - 1)] + 1;
return ans;
}
连续子串的和
437 路径总和III
给定一个二叉树,它的每个结点都存放着一个整数值。
找出路径和等于给定数值的路径总数。
路径不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
二叉树不超过1000个节点,且节点数值范围是 [-1000000,1000000] 的整数。
示例:
root = [10,5,-3,3,2,null,11,3,-2,null,1], sum = 8
返回 3。和等于 8 的路径有:
- 5 -> 3
- 5 -> 2 -> 1
- -3 -> 11
做法1 同下面方法2,维护一个nums[i]表示的是从0开始到元素i的目标总和,那么元素i到j的和为num[j + 1] - nums[i]
一定不要忘记减去0的情况,同下面的给0,1赋初始值。
public int pathSum(TreeNode root, int sum) {
return helper(root, sum, 0, new int[1000]);
}
public int helper(TreeNode root, int sum, int curLevel, int[] total){
if (root == null) return 0;
if (curLevel == 0) total[0] = root.val;
else {
total[curLevel] = total[curLevel - 1] + root.val;
}
int n = 0;
//这一步不要忘记
if (total[curLevel] == sum) n++;
for (int i = curLevel - 1; i >= 0; --i){
if (total[curLevel] - total[i] == sum){
n++;
}
}
int l = helper(root.left, sum, curLevel + 1, total);
int r = helper(root.right, sum, curLevel + 1, total);
total[curLevel] = 0;
return n + l + r;
}
方法2、同下面方法3,利用一个map,map的key是当前元素的总和,map的value是这个总和出现的个数。一定不要忘记赋0,1的初始值
public int pathSum(TreeNode root, int sum) {
HashMap<Integer, Integer> map = new HashMap<>();
map.put(0, 1);
return helper(root, sum, 0, map);
}
public int helper(TreeNode root, int sum, int total, HashMap<Integer, Integer> map){
int n = 0;
if (root == null) return 0;
total += root.val;
n += map.getOrDefault(total - sum, 0);
map.put(total, map.getOrDefault(total, 0) + 1);
int l = helper(root.left, sum, total, map);
int r = helper(root.right, sum, total, map);
map.put(total, map.get(total) - 1);
return n + l + r;
}
560 和为K的子数组
给定一个整数数组和一个整数 k,你需要找到该数组中和为 k 的连续的子数组的个数。
示例 1 :
输入:nums = [1,1,1], k = 2
输出: 2 , [1,1] 与 [1,1] 为两种不同的情况。
本题不能使用滑动窗口,因为里面得值有可能是负值,每次移动并不确定是增加还是减少。
方法1:依次遍历每个元素,并向后累加,遇到和为k则输出个数。
方法2:使用nums[i]记录从0开始到元素i得和,那么元素i到j的和就为:nums[j + 1] - nums[i],和方法一一样同样需要n方的复杂度。
方法3:在方法2的基础上,维护一个map,记录从0开始到当前元素的总和出现的个数。同时,sum表示的是从0到i的总和,k表示的是目标总和,那么sum - k这个数只要在之前的map中存在,比如从0到j的和是sum - k, 那么就代表从元素j到元素i之间的和是k,采用这种方法即可将时间复杂度缩减为o(n)。
public class Solution {
public int subarraySum(int[] nums, int k) {
int count = 0, sum = 0;
HashMap < Integer, Integer > map = new HashMap < > ();
map.put(0, 1);
for (int i = 0; i < nums.length; i++) {
sum += nums[i];
if (map.containsKey(sum - k))
count += map.get(sum - k);
map.put(sum, map.getOrDefault(sum, 0) + 1);
}
return count;
}
}
利用当前数组记录信息
本方法适合于需要简单的hashmap可以记录信息的情况,可以直接在当前数组上进行信息记录,第i的正负。
41 缺失的第一个正数
给你一个未排序的整数数组,请你找出其中没有出现的最小的正整数。
示例 1:
输入: [1,2,0]
输出: 3
示例 2:
输入: [3,4,-1,1]
输出:
示例 3:
输入: [7,8,9,11,12]
输出: 1
public int firstMissingPositive(int[] nums) {
int n = nums.length;
boolean flag = false;
for (int i = 0; i < n; ++i){
if (nums[i] == 1){
flag = true;
break;
}
}
if (!flag) return 1;
for (int i = 0; i < n; ++i){
if (nums[i] <= 0 || nums[i] > n){
nums[i] = 1;
}
}
for (int i = 0; i < n; ++i){
int index = Math.abs(nums[i]) - 1;
if (nums[index] > 0) nums[index] = -nums[index];
}
int res = 0;
for (res = 0; res < n; ++res){
if (nums[res] >= 0){
break;
}
}
return res + 1;
}
链表深拷贝
138 复制带随机指针的链表
给定一个链表,每个节点包含一个额外增加的随机指针,该指针可以指向链表中的任何节点或空节点。
要求返回这个链表的 深拷贝。
我们用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示
示例 1:
输入:head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出:[[7,null],[13,0],[11,4],[10,2],[1,0]]
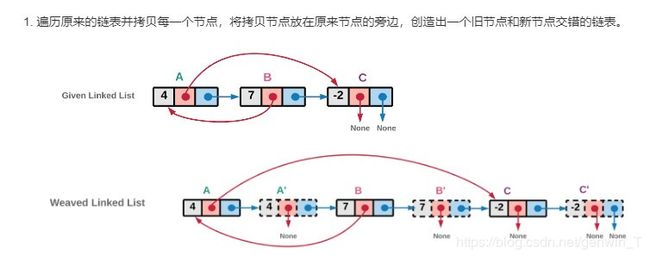
思路为3步:
1、在当前节点后面创建一个新的复制节点
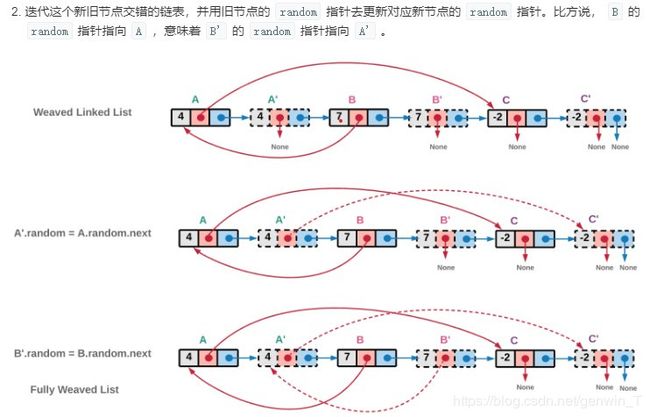
2、依据前面节点的random指针,更新后面节点的random指针
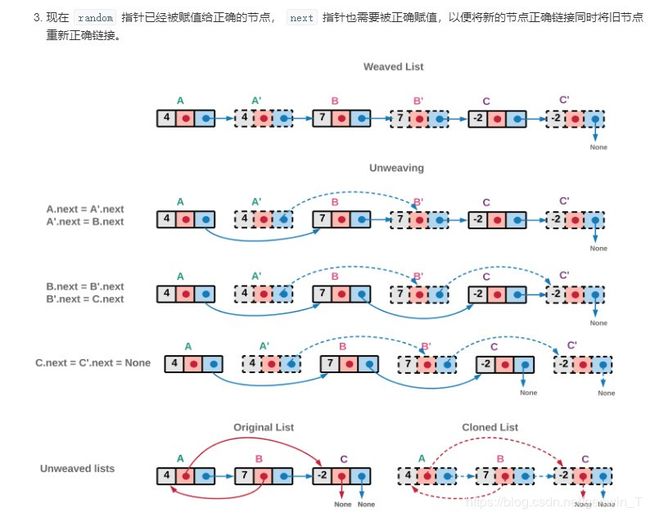
3、更新next指针
public Node copyRandomList(Node head) {
if (head == null) return null;
Node cur = head;
while (cur != null){
Node tempcur = cur;
cur = cur.next;
tempcur.next = new Node(tempcur.val);
tempcur.next.next = cur;
}
cur = head;
while (cur != null){
cur.next.random = cur.random == null ? null : cur.random.next;
cur = cur.next.next;
}
cur = head;
Node res = cur.next;
while (cur != null){
Node tempcur = cur, tempcopy = cur.next;
cur = cur.next.next;
if (cur == null){
tempcur.next = tempcopy.next = null;
} else {
tempcur.next = cur;
tempcopy.next = cur.next;
}
}
return res;
}
cmp函数的巧妙使用,判断a+b>b+a
179 最大数
给定一组非负整数,重新排列它们的顺序使之组成一个最大的整数。
示例 :
输入: [3,30,34,5,9]
输出: 9534330
可以用在排列组合的场景下
直接使用String类型,返回 b+a - a+b 即可
public String largestNumber(int[] nums) {
int n = nums.length;
String[] snum = new String[nums.length];
for (int i = 0; i < n; ++i){
snum[i] = String.valueOf(nums[i]);
}
Arrays.sort(snum, new Comparator<String>(){
@Override
public int compare(String o1, String o2) {
String a = o1 + o2;
String b = o2 + o1;
return b.compareTo(a);
}
});
if (snum[0].equals("0")) return "0";
String res = new String();
for (String s : snum){
res += s;
}
return res;
}
判断素数
如何找到一定范围内的所有素数:
对于从2开始的每一个素数,都将上面所以可达的非素数标记。
为了保证不会重复标记,内圈可以从i*i开始(比如3的话2×3已经被2标记过了,因此直接从3×3开始就可以了
public int countPrimes(int n) {
boolean[] isPrime = new boolean[n];
Arrays.fill(isPrime, true);
for (int i = 2; i * i < n; ++i){
if (isPrime[i]){
for (int j = i * i; j < n; j += i){
isPrime[j] = false;
}
}
}
int res = 0;
for (int i = 2; i < n; ++i){
if (isPrime[i]) res++;
}
return res;
}
这个算法的时间复杂度为n*loglog n
杂项
5 最长回文子串
一共是2*n-1中展开,即中间项为数和中间项为空的情况,进行遍历即可
19 删除链表的第n个节点
首先定义两个首节点l1,l2,指向头节点。然后定义一个节点l3等于head并向后next n次,l3和其中一个l2依次往后next,当l3为null的时候表示l2的next就是要删除的节点,然后让l2=next.next即可,最后输出l1.next
要注意一点是,只能new一个l1,然后让l2 = l1,不能两个都new,否则删除的节点为第一个节点时候,l2的更改不会影响到l1。
l1 = l2的定义表示两个即为同一个节点,一个的更改会影响到另一个,但是如果new两个新的话,两个互不影响。
20 有效的括号
对每一对括号建立map对,然后利用栈对括号进行判断,栈的性质十分符合括号的判断性质
22 括号生成
dfs:
public List<String> generateParenthesis(int n) {
List<String> res = new ArrayList<>();
if (n == 0) return res;
dfs("", n, n, res);
return res;
}
public void dfs(String cur, int left, int right, List<String> res){
if (left == 0 && right == 0){
res.add(cur);
return;
}
if (left > right || left < 0 || right < 0) return;
dfs(cur + "(", left - 1, right, res);
dfs(cur + ")", left, right - 1, res);
}
}
bfs:
class Node{
private String cur;
private int left;
private int right;
Node(String cur, int left, int right){
this.cur = cur;
this.left = left;
this.right = right;
}
}
public List<String> generateParenthesis(int n) {
List<String> res = new ArrayList<>();
if (n == 0) return res;
Queue<Node> queue = new LinkedList<>();
queue.offer(new Node("", n, n));
while (!queue.isEmpty()){
Node curNode = queue.poll();
if (curNode.left == 0 && curNode.right == 0){
res.add(curNode.cur);
}
if (curNode.left > 0){
queue.offer(new Node(curNode.cur + "(", curNode.left - 1, curNode.right));
}
//左边可以随便加,右边不行
if (curNode.right > 0 && curNode.left < curNode.right){
queue.offer(new Node(curNode.cur + ")", curNode.left, curNode.right - 1));
}
}
return res;
}
动态规划
dp[i]表示i对括号可能的情况
状态转移方程为
dp[i] = “(” + dp[x] + “)” + dp[i - 1 - x];
里面是0,外面就是i- 1 ,以此来列举可能的)出现的位置
public List<String> generateParenthesis(int n) {
if (n == 0) return new ArrayList<>();
//dp[i] 表示的是i对括号可能的情况
List<List<String>> dp = new ArrayList<>(n);
List<String> dp0 = new ArrayList<>();
dp0.add("");
dp.add(dp0);
for (int i = 1; i <= n; ++i){
List<String> cur = new ArrayList<>();
//要去除掉正在进行计算的i,所以括号和是i-1
for (int j = 0; j < i; ++j){
List<String> str1 = dp.get(j);
List<String> str2 = dp.get(i - 1 - j);
for (String s1 : str1){
for (String s2 : str2){
cur.add("(" + s1 + ")" + s2);
}
}
}
dp.add(cur);
}
return dp.get(n);
}
31 下一个排列
我们希望下一个数比当前数大,这样才满足“下一个排列”的定义。因此只需要将后面的大数与前面的小数交换,就能得到一个更大的数。比如 123456,将 5 和 6 交换就能得到一个更大的数 123465。
我们还希望下一个数增加的幅度尽可能的小,这样才满足“下一个排列与当前排列紧邻“的要求。为了满足这个要求,我们需要:
在尽可能靠右的低位进行交换,需要从后向前查找
将一个尽可能小的大数与前面的小数交换。比如 123465,下一个排列应该把 5 和 4 交换而不是把 6 和 4 交换
将大数换到前面后,需要将大数后面的所有数重置为升序,升序排列就是最小的排列。以 123465 为例:首先按照上一步,交换 5 和 4,得到 123564;然后需要将 5 之后的数重置为升序,得到 123546。显然 123546 比 123564 更小,123546 就是 123465 的下一个排列
因此,第一步就是从右边找到第一个比左边数大的数flag,如果这个数已经到了左边,说明这个排列是最大数,全部交换过来就可以了。
第二步,将flag及之后的数全部重新按从小到大的顺序排列
第三步,找到其中第一个比flag之前数大的数并交换即可。
32 最长有效括号
1、利用括号的性质左右各扫描一道
public int longestValidParentheses(String s) {
int maxLen = 0, left = 0, right = 0;
for (int i = 0; i < s.length(); ++i){
if (s.charAt(i) == '('){
left++;
} else {
right++;
}
if (left == right){
maxLen = Math.max(maxLen, 2 * right);
} else if (right > left){
right = left = 0;
}
}
left = right = 0;
for (int i = s.length() - 1; i >= 0; --i){
if (s.charAt(i) == '('){
left++;
} else {
right++;
}
if (left == right){
maxLen = Math.max(maxLen, 2 * right);
} else if (right < left){
right = left = 0;
}
}
return maxLen;
}
2、动态规划
dp[i]表示的是前i项中最大的括号数量,且只在")“处统计
3、栈
遇到”(“则在栈中添加当前下标,遇到”)“则删除,当前的下标减栈顶的数字就是最大长度。
栈需要判断,以免遇到连续的”)"导致空栈。
130 被围绕的区域
一般情况下还是用dfs比较好,dfs递归传参简便。bfs除了写起来麻烦,好像速度也比dfs要慢一些。
189 旋转数组
给定一个数组,将数组中的元素向右移动 k 个位置,其中 k 是非负数。
示例 1:
输入: [1,2,3,4,5,6,7] 和 k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右旋转 1 步: [7,1,2,3,4,5,6]
向右旋转 2 步: [6,7,1,2,3,4,5]
向右旋转 3 步: [5,6,7,1,2,3,4]
方法一:暴力移动
方法二:环形更换,对于每一个位置向后移动k的距离,最后总会回到原点,然后移动下一个。这个方法有两个要点:第一、使用一个count记录移动数字的总数,当count==n的时候结束循环,表明所有的数字都已经移动过了。第二、使用next=(cur+k)%n来表示下一个数字的位置,这种方法可以使后面的数字直接换到前面来。
public void rotate(int[] nums, int k) {
int n = nums.length;
k = k % n;
int count = 0;
for (int start = 0; count < n; ++start){
int cur = start;
int prev = nums[start];
do {
int next = (cur + k) % n;
int temp = nums[next];
nums[next] = prev;
prev = temp;
cur = next;
count++;
} while (start != cur);
}
}
方法三:3次反转。
e.g. 1 2 3 4 5 6 7 k=3
第一次反转:7 6 5 4 3 2 1
第二次反转前k个数:5 6 7 4 3 2 1
第三次反转后面的数:5 6 7 1 2 3 4
448 找到所有数组中消失的数字
给定一个范围在 1 ≤ a[i] ≤ n ( n = 数组大小 ) 的 整型数组,数组中的元素一些出现了两次,另一些只出现一次。
找到所有在 [1, n] 范围之间没有出现在数组中的数字。
您能在不使用额外空间且时间复杂度为O(n)的情况下完成这个任务吗? 你可以假定返回的数组不算在额外空间内。
示例:
输入:
[4,3,2,7,8,2,3,1]
输出:
[5,6]
将下标出现的位置的数字用负数进行标记
最后遍历一遍数组,找到为正数的数字即可
public List<Integer> findDisappearedNumbers(int[] nums) {
List<Integer> list = new ArrayList<>();
// int[] has = new int[nums.length];
// for (int num : nums){
// has[num - 1]++;
// }
// for (int i = 0; i < nums.length; ++i){
// if (has[i] == 0){
// list.add(i + 1);
// }
// }
for (int i = 0; i < nums.length; ++i){
int index = Math.abs(nums[i]) - 1;
if (nums[index] > 0) nums[index] = -nums[index];
}
for (int i = 0; i < nums.length; ++i){
if (nums[i] > 0){
list.add(i + 1);
}
}
return list;
}
581 最短无序连续子数组
本题的关键点在于,找到乱序中最大的值(对应在数组中最后面的位置),最小的值(对应数组中最前面的位置)。
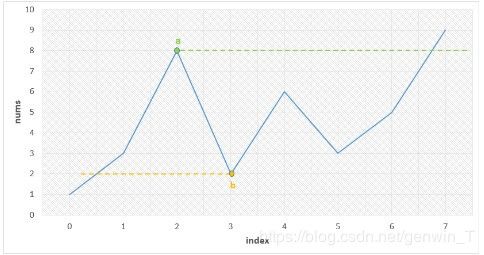
主要有三种方法:
1、直接复制一份数组然后排序,挨个对比找到乱序的位置即可输出长度。
2、利用栈,从左向右,如果一直是升序就压入栈(栈中存放的是下标),否则遇到当前数字比栈顶元素对应的值小就弹出,最后栈顶元素就是最左边值得位置。
同样,从右向左进行一遍遍历,得到最大得值在数列中得位置,即可输出长度。
3、找到波峰中最大得值,再扫描得到波谷中最小得值,在进行比较即可。
乱序得点一定是波峰和波谷。和162比较类似。
621 任务调度器
给定一个用字符数组表示的 CPU 需要执行的任务列表。其中包含使用大写的 A - Z 字母表示的26 种不同种类的任务。任务可以以任意顺序执行,并且每个任务都可以在 1 个单位时间内执行完。CPU 在任何一个单位时间内都可以执行一个任务,或者在待命状态。
然而,两个相同种类的任务之间必须有长度为 n 的冷却时间,因此至少有连续 n 个单位时间内 CPU 在执行不同的任务,或者在待命状态。
你需要计算完成所有任务所需要的最短时间。
输入: tasks = [“A”,“A”,“A”,“B”,“B”,“B”], n = 2
输出: 8
执行顺序: A -> B -> (待命) -> A -> B -> (待命) -> A -> B.
普通解法,排序,然后每次从最大的数字开始往里面放即可,每一轮放完都要重新排序一次。
或者原题解见LeetCode621官方题解
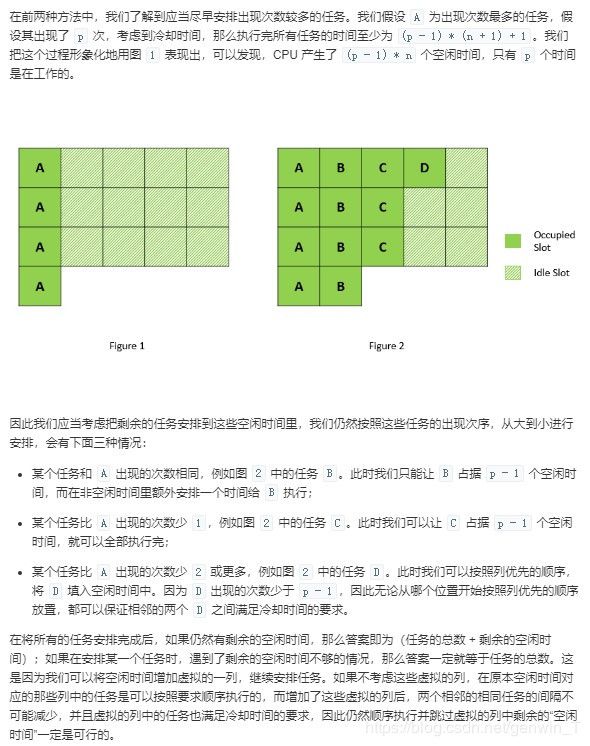
public int leastInterval(char[] tasks, int n) {
int time = 0;
int[] map = new int[26];
for (char c : tasks){
map[c - 'A']++;
}
Arrays.sort(map);
int maxVal = map[25] - 1, leftover = maxVal * n;
for (int i = 24; i >= 0 && map[i] > 0; --i){
leftover -= Math.min(map[i], maxVal);
}
return leftover > 0 ? leftover + tasks.length : tasks.length;
}
739 每日温度
利用栈的特性进行计算。栈中存放的是数组的下标。
如果当前元素比栈顶元素对应的值大,则出栈,值为i-栈顶元素。
否则,入栈。
最后把栈中的元素对应天数全部置0,已经遍历完成,后面不可能会有比当前元素更大的了。
面试题:寻找最大差
给定一串整数,要求找到两个数,满足下标大的数减下标小的数差值最大
方法:利用单调栈,递增,并记录最大值即可。
核心的思路为对于每一个最小值,都要找到后面最大的值减去他,然后将差值进行比较。
比如 6 3 7 1 4
max = 0;
1、6入栈。栈:6 max = 0
2、3入栈,比6小。6出栈,3入栈。栈:3 max = 0
3、7入栈。栈:3 7 max = 4
4、1入栈,3 7 出栈。栈:1 max = 4
5、4入栈。栈:1 4 max = MAX(max, 3) = 4;