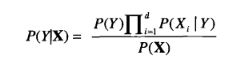常见分类方法

本文只对几种常见的分类方法做简单介绍，详细的讲解和算法网上有很多资源，文中会给出推荐链接。

Content

1.      决策树分类（链接：http://blog.csdn.net/github_36299736/article/details/52749999）

2.      基于规则分类

3.      最邻近分类（K-NN）

4.      朴素贝叶斯分类器

5.      人工神经网络

6.      支持向量机（SVM）

 

1. 基于规则的分类器

简单来说，基于规则的分类器就是使用一组“if… then …”的组合来进行分类的技术。通常用R =( r1˅ r2 ˅ … ˅ rk)来表示，其中 ri 就是分类的规则。

以上图为例，r1  类就可以用如下规则判断：

        If （胎生 = 否 & 飞行动物 = 是）then （类别 = 鸟类）

度量分类规则的质量可以用覆盖率（coverage）和准确率（accuracy）。覆盖率就是满足规则的记录数占总记录数的比例，准确率就是使用该规则正确分类的比例。

基于规则分类还有以下两个重要的规则：

        互斥规则（Mutually Exclusive Rule）和穷举规则（Exhaustive Rule）

互斥规则：规则集中不存在两条规则被同一条记录触发。简单说就是保证同一条记录不会同时属于两个类别。

穷举规则：对于属性值的任一组合，R中都存在一条规则加以覆盖。即每一条记录都保证能以其中一种规则加以分类。

这两个性质就可以保证每条记录被且仅被一条规则覆盖。但是实际情况下，分类器可能无法满足这两条性质。对于不能穷举的规则集，我们可以通过设定一个默认规则来覆盖不能被分类的记录。对于不互斥的规则集，我们可以通过建立优先级或者为规则加权等方式来解决。

 

2. 最邻近分类器

最邻近分类器是一种简单且常用的分类器。也就是我们常说的K-NN分类算法。它的原理非常简单，即根据与测试数据最近的K个点的类别，采用多数表决方案来确定该测试数据的分类。

以上图为例，1-最邻近（图a）中可以看到与测试数据最近的一个点为负，所以该测试点被指派到负类。2-最邻近（图b）中，与测试数据最近的两点为一正一负，可以随机选择其中一个类别。3-最邻近（图c）中，最近的三个点为两正一负，根据多数表决方案，该点被指派为正。

从上述例子中就可以看到该算法中k值的选取非常关键。K值太小，结果容易受到数据中噪声的影响从而产生过拟合。K值太大，容易导致误分类，因为结果可能会受到距离测试数据点非常远的数据的影响。（如下图）

算法描述如下：

也可以对不同距离的数据点进行加权，从而提高分类的准确率。

 

3. 朴素贝叶斯分类器

了解朴素贝叶斯分类，首先要知道贝叶斯定理，也就是我们比较熟悉的条件概率。参考：http://blog.csdn.net/github_36299736/article/details/52800394

朴素贝叶斯分类器的工作原理就是计算测试数据被分给各个类别的条件概率（后验概率），并将该记录指派给概率最大的分类。

让我们用之前在决策树分类中使用过的例子来分析：

假定一个测试数据，该测试数据的属性集可以表示为：X= {有房=否，婚姻状况=已婚，年收入=120k}，我们需要将该数据分类到两个类别之一，即 Y = {拖欠贷款=是，拖欠贷款=否}。那么我们需要做的就是分别计算两种分类情况下的后验概率 P (Y|X) 。 P1 = P (拖欠贷款 = 是|X) 和P2 = P (拖欠贷款 = 否|X) ，如果P1 >P2，则记录分类为拖欠贷款 = 是，反之分类为拖欠贷款 = 否。

朴素贝叶斯分类器更通常的表示方法：给定类标号 y，朴素贝叶斯分类器在估计条件概率时假设属性之间条件独立，若每个属性集（数据）包含d个属性X = { X1，X2，…，Xd } ，那么每个类Y的后验概率计算公式为：

由于P(X)是固定值，因此只要找出分子最大的类就可以了。

对于连续属性的条件概率，可以用以下两种方法来估计它的类条件概率:

1.      把连续的属性离散化，然后用相应区间来替代连续的属性值；

2.      假设连续变量服从某种概率分布（例如：高斯分布），然后使用训练数据估计分布的参数。

 

4. 人工神经网络（ANN）

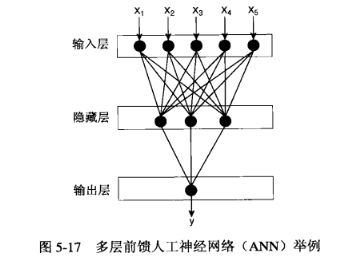
类似于人脑由神经元及轴突构成的结构，人工神经网络由相互连接的结点和有向链构成。最简单的ANN模型是感知器（perceptron）。

以上图为例，b即为一个感知器，其中，x1, x2, x3 分别为三个输入结点，在本例中表示三个输入的布尔值，还有一个输出结点。结点通常叫做神经元或单元。感知器中，每个输入结点都通过一个加权链连接到输出结点。加权链就像神经元间连接的强度，训练一个感知器模型就相当于不断调整链的权值，直到能拟合训练数据的输入输出关系为止。

感知器对输入加权求和，再减去偏置因子 t，然后考察得到的结果，得到输出值 ŷ。

上图中分类依据为如果三个输入值中至少两个0，y取-1，至少有两个1时，y取1. 它的感知器的输出计算公式如下：

更通用的数学表达方式是：

其中，w1, w2, …, wd 是输入链的权值，x1, x2, …, xd 是输入属性值。

还可以写成更简洁的形式：

其中，w0 = -t，x0 = 1. w · x 是权值向量 w 和输入属性向量 x 的点积。

 

多层人工神经网络

多层神经网络相比于感知器要复杂得多，首先，网络的输入层和输出层之间可能包含多个隐藏层，隐藏层中包含隐藏结点。这种结构就叫做多层神经网络。感知器就是一个单层的神经网络。

除此之外，网络还可以使用其他激活函数（如S型函数，双曲线正切函数，符号函数等）使得隐藏结点和输出结点的输出值和输入参数呈非线性关系。

直观上，我们可以把每个隐藏结点看成一个感知器，而每个感知器可以构造出一个超平面用于分类。如下图a中所构造的两个超平面。

ANN学习算法的目标函数是找出一组权值w，使得误差平方和最小：

 

对于激活函数是线性函数的情况，可以将ŷ =w · x 带入上式将其变成参数的二次函数，就可以找出全局最小解。当输出是参数的非线性函数的时候，可以采用梯度下降法来优化。

关于神经网络的更多内容，我推荐这一篇文章，来自知乎专栏，作者：YJango，链接：https://zhuanlan.zhihu.com/p/22888385

 

5. 支持向量机（SVM）

SVM是现在倍受关注的分类技术，可以很好地适用于高维数据。它的特点是，使用训练实例的一个子集来表示决策边界，该子集就是支持向量。那么为什么把一个决策边界叫做“向量”呢？首先从最大边缘超平面这个概念开始了解。

假设这是一个数据集，其中包含两类数据，分别用方块和圆来表示。非常直观地看到，我们很容易在两组数据之间找到无限个超平面（本例中是一条直线），使得不同类的数据分别在这个超平面的两侧。

但是，有一些超平面的选择在测试未知数据时的效果可能并不好，比如下图中的红色线：

可以看到，只要测试数据稍稍偏离一点，就容易导致分类错误。因此，我们要在这无数条分界线中找到一条最优解，使它到两边的边距最大。（如下图）

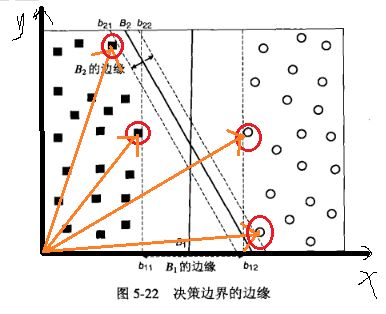
如果将这些数据点放在坐标系中，边缘的点可以以向量的形式来表示：

 

其中，用红色圈起来的数据点就是support vector，这也就是SVM这个算法名称的由来。

关于支持向量机，有一系列非常好的博客可以参考，作者：pluskid，链接：http://blog.pluskid.org/?page_id=683

 

其实常用分类方法还有很多，例如AdaBoost，以及不同分类方法的组合。本文只是参考书中内容对几种常见分类算法做了入门级介绍，可以根据实际的学习和工作需要做深入研究并择优使用。 感谢阅读。

 

参考：《数据挖掘导论》第五章 分类：其他技术