吴恩达深度学习——01神经网络和深度学习

    博客主要是用来作为学习报告和一些笔个人记记录所用。

    本文主要是对吴恩达深度学习课程的第一个大章“神经网络和深度学习”进行了学习后的一个个人笔记记录和以及个人总结。整个学习的过程，在视频学习（自己使用的是视频的文字版，否则会把视频经常暂停用来来思考字幕的含义，所以干脆用的文字版本）和编程学习中，个人觉得第一章整个过程学习下来，并不是很花时间，而且也比较简单，主要花时间的是编程的过程，因为在网易云上的视频是没有课后作业的，因此我找到的作业是网上其他人总结的所有的课程的作业。也是通过作业，才能对看似简单的课程内容，有一个更加实践性的理解，编程的过程是不可或缺的。

一、神经网络的概念

主要是一些概念性的介绍，略

二、神经网络基础

    这一部分主要是讲解了逻辑回归（Logistic Regression），相当于是神经网络的一个引入小节吧，对于后面两节来讲，这一节的内容是讲述了如何构建后两节的其中的一个神经单元。Logistic Regression是一个用于二分类的算法。Logistic Regression的主要表达式为yhat=wx+b，整个过程其实是要实现对w，b两个值的最佳值求解，并将其用作最后的预测式。可以将Logistic Regression分为前向传播(forward propagation)和后向传播(backward propagation)。

    Logistic Regression的前向传播构建主要有如下几个式子：

    （1）、z=wx+b, a=sigmoid(z)（其中的sigmoid只是激活函数(activation function)一种）

    （2）、L(a,y)=-y*log(a)-(1-y)*log(1-a)

    （3）、

    逻辑回归可以认为是一个非常简单的神经网络，第一个公式是在初始化w，b后，对样本值，即训练集进行z的计算，并将其代入到激活函数，得到a值。

    首先第一个式子，其中的z值很明显，是一个线性函数，而a的求解需要使用激活函数(activation function)，激活函数的作用是加入非线性因素，因为假如没有非线性函数的参与，那么整个过程都将是一个线性过程，那么对于模型的表达将是不够的。激活函数对整个过程加入了非线性因素，让神经网络可以逼近任何非线性函数。上述的这个原因呢，算是对这么一个激活函数作用的一个最直观的解释。但是现在可能对其理解不够，也不做深究，也可能在接下来的学习会遇到，可能对其有更加深刻的理解。我们一般使用的激活函数有四种：sigmoid，ReLU（修正线性单元）,tanh,leaky ReLU，对四种的比较详情可以查看其他博文。

    其中第二个式子，从已经完成了式子来看，理解上也不是十分的困难，因为是二分类问题，所以将y=0或者是1代入到式子中，便可以比较直观的感受到它想表达的一种思想。但是毕竟是数学式子，因此从最根本的原理上来看会对理解式子有根本性的帮助，L式子与极大似然估计有关，在此不详细叙述，可以参看其他学习博文：https://blog.csdn.net/programmer_wei/article/details/52072939。

    第三个式子是Logistic Regression的损失函数(Cost function)，相当于此时的w，b的值所带来的代价值，当然，这个值是越小越好，J值越小，表示w，b的值约契合训练集。

    Logistic Regression的后向传播的构建：

    

    

    梯度下降法：

     

    整个后向传播的思想是利用梯度下降法，来求损失函数的局部最小，当达到局部最小的时候，即得到我们想要的w，b值，并且用w，b来进行测试集的预测。

    总结：在这一节的学习里，原理部分还比较好理解，编程过程中，会有一些小问题，大多是属于一些数据处理、数据shape和编程的函数理解上的问题。比较需要注意的是，因为数据量大与一些其他的数据处理原因，需要将上述的公式进行向量化处理，一切的操作需要的都是向量化的操作，这样会解决了使用循环耗时严重的问题，同时也让代码变得简洁，但是，需要注意的就是编程计算过程中，对于每一个数据的shape需要十分的注意。吴恩达在视频中说他会用一张纸在编程过程中记录下计算过程数据的维度即shape值，这一点自己很庆幸与其是不谋而合。

三、浅层神经网络

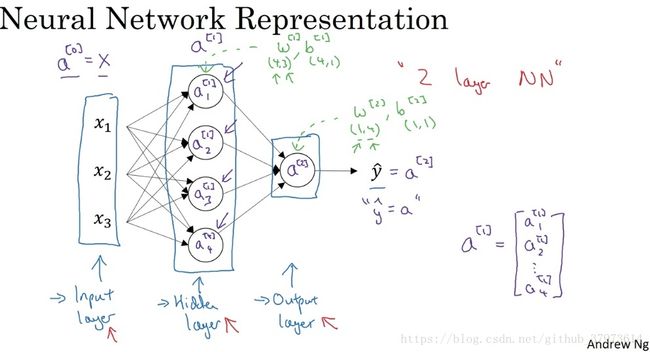
    这一部分呢，是介绍了比较浅层的神经网络（两层，第0层输入层不计入神经网络层）。在这一节中，向量化的体现会更加的明显。在python里，主要的向量化操作库是NumPy，对我们的运算提供了极大的方便。

   1、 简单神经网络

    

    在这里，需要基本的信息图中都有，其中每一个神经元单位就相当于是一个逻辑回归的操作，所以在这里，可以回头理解下了逻辑回归可以归纳为一个非常简单的神经网络。每一层会有w和b的向量表示，其中w的shape值为（n_L, n_L-1），而b的shape为（n_L, 1），比如在这个简单神经网络，将会有两对w,b，其中第一对的shape分别是（4，3），（4，1），第二对的shape是（1， 4），（1， 1），这样直观来看还是比较简单的。

    2、上一节讲述的四种激活函数

    

    对于上面的四种激活函数，有一个简单的比较：

    sigmoid函数和tanh函数，在隐藏层中，tanh函数表现要好于sigmoid函数，因为tanh的取值范围是[-1, 1]，输出分布在0值附近，均值为0，从隐藏层到输出层数据起到了归一化（均值为0）的效果。在输出层，对二分类的任务的输出取值为{0，1}，故一般会选择sigmoid函数。

    但是当sigmoid和tanh函数在自变量很大的时候，梯度会很小。故在实际应用中， 要是自变量也即神经元中|z|值尽可能落在0附近。

    ReLU弥补了前两者的缺陷，当z>0时，梯度始终为1，从而提高了神经网络基于梯度算法的运算速度。当z<0时，梯度一直为0。Leaky ReLU保证在z<0的时候，梯度仍然不为0，而是一个比较晓得值，这个值需要我们自己去尝试确定。

    3、神经网络的整个反向传播公式以及代码向量化

    

    上图中的g函数表示的激活函数，而具体是哪一种激活函数，则根据具体的代码实现来确定。整个梯度求解过程，主要使用了一个链式求导法则，虽然这一部分的公式的推导在吴恩达视频中将其定义为整个学习过程中比较麻烦的地方，但是对于高中大学求导身经百战的中国学子来说，应该不算是什么大问题。但是这里需要注意的是，dz符号表示J（Cost function）对z的求导，其余的类似。这里这样写，主要是为了一个编程上的方便，所以这里是需要十分十分注意的地方，否则会因为潜意识里将其当作微分。

    总结：

    在整个过程中，有一个需要注意的点。如果两个隐藏神经元的参数设置大小相同，那么两个神经元对输出的影响也是相同，所以在接下来的一系列运算中，这两个神经元所带来的数据完全是一样的，与一个神经元的作用将是一样的。因此，在初始化时，对w需要随机的初始化，而b不存在对称性的问题可以直接设置为0。所以编程中为了令结果固定，直接使用了随机数种子来固定每一次的随机数序列。

    我们尽量需要令z=wx+b的z值小一些，处于0的附近，因为在0的附近梯度会比较大， 更够大大提高算法的更新速度。而如果w设置的太大，得到的梯度会很小，训练过程会变得很慢。不过ReLU和Leaky ReLU作为激活函数时，不存在这样子的问题，因为在大于0的时候，梯度均为1。

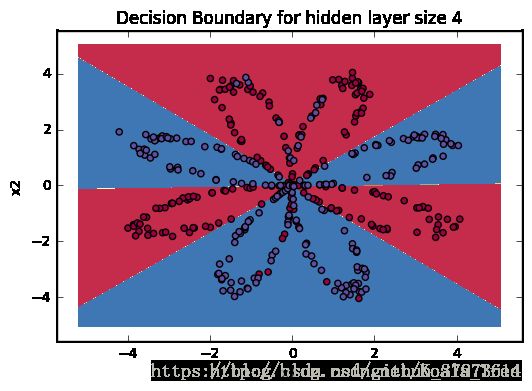
    在编程中，遇到了一个问题，在计算L（a，y）时，log函数中有一个数值非法的问题，最终造成了输出全部都为Nan。最终这个地方的问题是测试的时候一个自带文件里的y值初始化出现了负值。这些地方还是需要注意的，问题不算很难解决，但是能注意的地方还是注意下吧。整个编程便是对整个浅层神经网络的一步步实现，在对整个编码的实现过程中，还是能够学到很多东西的，是在理论之上学习到很多小技巧之类的，以及对python相关库的理解。最后添加一副对比图来显示神经网络的强大。

    

    四：深度神经网络

    深度神经网络（DNN）的隐藏层会比较多，这样计算量也将会随之增加。首先必须要对”深度“要有一个理解，为什么需要”深度“。对于人脸识别，神经网络的第一层从原始图片中提取人脸的轮廓和边缘，每个神经元学习到不同边缘的信息；网络的第二层将第一层学到的边缘信息组合起来，形成人脸的一些局部的特征，例如眼睛、嘴巴等；后面的基层逐步将上一层的特征组合起来，形成人脸的模样。随着神经网络层数的增加，特征也从原来的边缘逐步扩展为人脸的整体，由整体到局部，由简单到复杂。层数越多，那么模型学习的效果也就越精确。

    对于语音识别，第一层神经网络可以学习到语音发音的一些音调，后面更深层次的网络可以检测到基本的音素，砸到单词信息，逐渐加深可以学习到短句、句子。

    所以从上面的两个例子可以看出随着神经网络的深度加深，模型能学习到更加复杂的问题，功能也更加强大。

    在这一届，因为只有层数的加深，在理论上与上一节差不多，因此主要是变成上有一些需要注意的技巧。比如在每一层的前向传播时用一个cache临时变量将w，b，z，a信息保存，以方便在后向传播中利用。

    这里有一个参数和超参数的概念，参数即我们在过程中想要模型学习到的信息w，b。而超参数是控制参数输出值的一些网络信息，也就是超参数的改变会导致最终得到的参数w，b的改变。整个过程中有几个重要的超参数，比如学习速率，即在梯度下降时的梯度系数，迭代次数，隐藏的层数，每一层的神经元个数，激活函数的选择，这些都是需要经过经验和时间尝试才能找到一个比较好的值。

    

    本章学习的总结：整个章节的学习过程先通过视频资料学习基本的理论，再通过编程来学习理论的应用，一步步的推进，整个过程下来，对这一章的内容有了一定的了解。虽然是很简单的一些基础知识，但是也让自己能如此轻松的初步学习了深度学习，在此很感谢Ng提供这么好的课程。接下来的这一周就是对更加复杂的卷积审计网络的学习了

文章部分内容参考：https://zhuanlan.zhihu.com/p/35333489