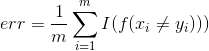机器学习笔记——ROC曲线

1.性能度量简介

在对学习器的泛化 能力进行评估是模型泛化的能力，即要用到机器学习的性能度量，不同的性能度量往往会导致不同的评判结果，这意味着模型的好坏是相对的，什么样的模型是好的，不仅取决于算法和数据，还决定于任务的要求。

分类任务重最常用的是准确度(accuracy)及错误率(error rate):

上面两个度量经常用，但对于不平衡的数据集不适应。

首先做一些定义：

• TN (True Negative):case was negative and predicted negative
• TP (True Positive):case was positive and predicted positve
• FN (False Positive):case was negative but predicted positve;
• FP (False Positve): case was negative but predicted positve

精度(Precision)也称为查准率

召回率(recall)也称为查全率：

查准率是确定分类器中断言为正样本的部分其实际中属于正样本的比例，精度越高则假的正例就越低，召回率则是被分类器正确预测的正样本的比例。两者是一对矛盾的度量，其可以合并成另一个度量，F1度量：

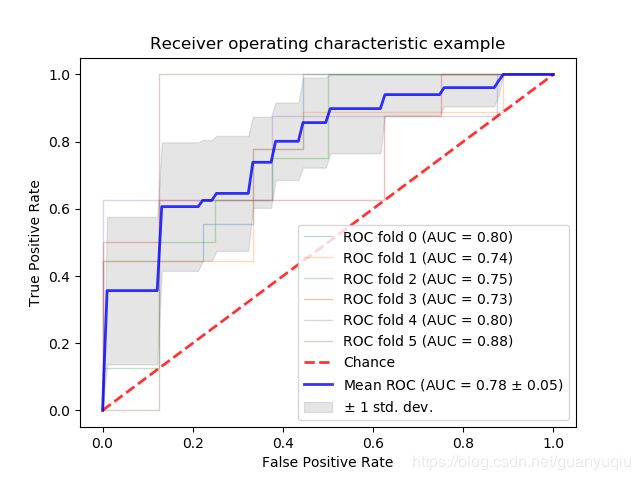
ROC(receiver oprating characteristic)接受者操作特征，其显示的分类器的真正率和假正率之间的关系，ROC曲线有助于比较不同分类器的相对性能，ROC曲线的面积为AUC(area under curve),其面积越大则分类的性能越好，理想的分类器auc=1.

PR(precision recall)曲线表现的是precision和recall之间的关系

2.python sklearn 部分函数简介

2.1 Sklearn 数据划分方法

K折交叉验证

kFold,GroupKFold, StratifiedKFold

1. 将全部验证集S分为k个不想交的子集，假设S中的训练样例个数为m，那么每一个子集有m/k个训练样例，相应的子集称为{s1,s2.....,sk};
2. 每次从分好的子集里面，拿出一个作为测试集，其它k-1个作为训练集；
3. 在k-1个训练集上训练出学习器模型；
4. 把这个模型放到测试集上，得到分类率；
5. 计算k次求得的分类率的平均值，作为该模型或者假设函数的真实分类率；

这个方法充分利用了所有样本，但计算比较繁琐，需要训练k次，测试k次。

2.2 sklearn  ROC参数调用介绍

ROC参数说明网址：https://scikit-learn.org/stable/modules/generated/sklearn.metrics.roc_curve.html#sklearn.metrics.roc_curve

sklearn.metrics.roc_curve(y_true, y_score, pos_label=None, sample_weight=None, drop_intermediate=True)

y_true:数组，shape=[样本数]

在范围{0,1}或{-1,1}中真正的二进制标签，如果标签不是二进制的，则应该显示地给出pos_label;

y_score:数组， shape=[样本数]

目标得分，可以是正类的概率估计，或者是决定的非阈值度量(在某些分类器上由"decision_function"返回)；

pos_label:int or str,标签被认为是正的，其它的被认为是负的；

sample_weight:样本的权重；

drop_intermediate:boolean, optional(default = True)

是否放弃一些不出现在绘制的ROC曲线上的次优阈值，这有助于创建更轻的ROC曲线；

Returns:

fpr:arry, shape =[>2]                  Increasing FP

tpr: arry, shape=[>2]                  Increasing TP

thresholds: arry, shape=[n_thresholds]

3.例子

"""
=============================================================
Receiver Operating Characteristic (ROC) with cross validation
=============================================================

Example of Receiver Operating Characteristic (ROC) metric to evaluate
classifier output quality using cross-validation.

ROC curves typically feature true positive rate on the Y axis, and false
positive rate on the X axis. This means that the top left corner of the plot is
the "ideal" point - a false positive rate of zero, and a true positive rate of
one. This is not very realistic, but it does mean that a larger area under the
curve (AUC) is usually better.

The "steepness" of ROC curves is also important, since it is ideal to maximize
the true positive rate while minimizing the false positive rate.

This example shows the ROC response of different datasets, created from K-fold
cross-validation. Taking all of these curves, it is possible to calculate the
mean area under curve, and see the variance of the curve when the
training set is split into different subsets. This roughly shows how the
classifier output is affected by changes in the training data, and how
different the splits generated by K-fold cross-validation are from one another.

.. note::

    See also :func:`sklearn.metrics.roc_auc_score`,
             :func:`sklearn.model_selection.cross_val_score`,
             :ref:`sphx_glr_auto_examples_model_selection_plot_roc.py`,

"""
print(__doc__)

import numpy as np
from scipy import interp
import matplotlib.pyplot as plt

from sklearn import svm, datasets
from sklearn.metrics import roc_curve, auc
from sklearn.model_selection import StratifiedKFold

# #############################################################################
# Data IO and generation

# Import some data to play with
iris = datasets.load_iris()
X = iris.data
y = iris.target
X, y = X[y != 2], y[y != 2]
n_samples, n_features = X.shape

# Add noisy features
random_state = np.random.RandomState(0)
X = np.c_[X, random_state.randn(n_samples, 200 * n_features)]

# #############################################################################
# Classification and ROC analysis

# Run classifier with cross-validation and plot ROC curves
cv = StratifiedKFold(n_splits=6)   #数据划分
classifier = svm.SVC(kernel='linear', probability=True,
                     random_state=random_state)

tprs = []
aucs = []
mean_fpr = np.linspace(0, 1, 100)

i = 0
for train, test in cv.split(X, y):
    probas_ = classifier.fit(X[train], y[train]).predict_proba(X[test])
    # Compute ROC curve and area the curve
    fpr, tpr, thresholds = roc_curve(y[test], probas_[:, 1])
    tprs.append(interp(mean_fpr, fpr, tpr))
    tprs[-1][0] = 0.0
    roc_auc = auc(fpr, tpr)
    aucs.append(roc_auc)
    plt.plot(fpr, tpr, lw=1, alpha=0.3,
             label='ROC fold %d (AUC = %0.2f)' % (i, roc_auc))

    i += 1
plt.plot([0, 1], [0, 1], linestyle='--', lw=2, color='r',
         label='Chance', alpha=.8)

mean_tpr = np.mean(tprs, axis=0)
mean_tpr[-1] = 1.0
mean_auc = auc(mean_fpr, mean_tpr)
std_auc = np.std(aucs)
plt.plot(mean_fpr, mean_tpr, color='b',
         label=r'Mean ROC (AUC = %0.2f $\pm$ %0.2f)' % (mean_auc, std_auc),
         lw=2, alpha=.8)

std_tpr = np.std(tprs, axis=0)
tprs_upper = np.minimum(mean_tpr + std_tpr, 1)
tprs_lower = np.maximum(mean_tpr - std_tpr, 0)
plt.fill_between(mean_fpr, tprs_lower, tprs_upper, color='grey', alpha=.2,
                 label=r'$\pm$ 1 std. dev.')

plt.xlim([-0.05, 1.05])
plt.ylim([-0.05, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.savefig("roc.png")

结果图：