次梯度法
在前文梯度下降法(一)从导数到梯度下降法的基本逻辑中指出,当函数梯度不存在时候,梯度下降法失效,而次梯度法则是凸优化中解决此类状况的一种有效方法。
一、基本定义
为了介绍次梯度的概念,首先需要引入次导数、次微分等概念。这些概念源于导数、微分,但又有显著的区别。
1. 次导数
下图中的一元函数均为凸函数,但在其拐点处不可导。观察拐点A、B处的直线,按照其与原始函数的位置关系,可分为如下两大类:
1)与原始函数相交,在不同自变量区间内,直线与原始函数的上下关系不确定
2)与原始函数在某点相交,但除了接触的若干点外,均在原始函数的下方
对于上述的第二类直线的导数,我们可以为原始函数在该点处的次导数。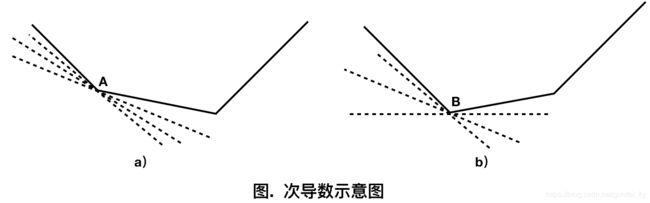
用更加符号化的语言描述:对于一元函数 y = f ( x ) y=f(x) y=f(x),在其上的点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)处,若存在某个常数 c c c,使得在对于整个定义域内的 x x x,均满足 f ( x ) − f ( x 0 ) ≥ c ( x − x 0 ) f(x)-f(x_0)\ge c(x-x_0) f(x)−f(x0)≥c(x−x0),则值 c c c就是函数 f ( x ) f(x) f(x)在点 x 0 x_0 x0处的一个次导数。
从几何直观上看(如上图):次导数方向的直线均在原始函数的下方。次导数方向的直线可视为原始函数的一个下界函数。
显然,对于一个一元凸函数,其在某点处的次导数往往存在多个(无穷个),这些次导数的集合即为次微分。特殊的,若该点可微,则次导数唯一,即为导数。
以函数 f = ∣ x ∣ f=|x| f=∣x∣在 ( 0 , 0 ) (0,0) (0,0)点处的次导数为例:
此时函数的左导数为: lim x → − x 0 f ( x ) − f ( x 0 ) x − x 0 = − 1 \lim\limits_{x\rightarrow -x_0}\frac{f(x)-f(x_0)}{x-x_0}=-1 x→−x0limx−x0f(x)−f(x0)=−1
函数的右导数为: lim x → + x 0 f ( x ) − f ( x 0 ) x − x 0 = 1 \lim\limits_{x\rightarrow +x_0}\frac{f(x)-f(x_0)}{x-x_0}=1 x→+x0limx−x0f(x)−f(x0)=1
因此其次导数的取值范围为 [ − 1 , 1 ] [-1,1] [−1,1],这种计算方式可推广到其它函数。
2. 次梯度
将一元凸函数中的次梯度在多元凸函数中进行推广,则得到次梯度的数学概念:对于多元凸函数 y = f ( x ) y=f(\boldsymbol x) y=f(x),在其上的点 ( x 0 , y 0 ) (\boldsymbol x_0,\boldsymbol y_0) (x0,y0)处,若存在某个向量 g \boldsymbol g g,使得在对于整个定义域内的 x \boldsymbol x x,均满足 f ( x ) − f ( x 0 ) ≥ g T ( x − x 0 ) f(\boldsymbol x)-f(\boldsymbol x_0)\ge \boldsymbol g^T(\boldsymbol x-\boldsymbol x_0) f(x)−f(x0)≥gT(x−x0),则向量 g \boldsymbol g g就是函数 f ( x ) f(\boldsymbol x) f(x)在点 x 0 \boldsymbol x_0 x0处的一个次梯度。
从几何直观上,次梯度向量构成的超平面始终在原始函数的下方。次梯度向量构成的超平面可视为原始函数的一个下界函数。
对于多元凸函数,其在任意点处的次梯度是始终存在的。特殊的,当函数在该点处可微时,次梯度即为梯度 ∇ f ( x 0 ) \nabla f(\boldsymbol x_0) ∇f(x0)。
3. 次微分
次微分可视作次梯度的集合: ∂ f ( x 0 ) = { g ∣ f ( x ) − f ( x 0 ) ≥ g T ( x − x 0 ) } \partial f(\boldsymbol x_0)=\{\boldsymbol g|f(\boldsymbol x)-f(\boldsymbol x_0)\ge \boldsymbol g^T(\boldsymbol x-\boldsymbol x_0)\} ∂f(x0)={g∣f(x)−f(x0)≥gT(x−x0)}
次微分有如下的重要性质和运算方法:
1)若凸函数 f ( x ) f(\boldsymbol x) f(x)在 x ∗ \boldsymbol x^* x∗处取得最小值,则向量 0 \boldsymbol 0 0必为 x ∗ \boldsymbol x^* x∗处的次梯度,即 0 ∈ ∂ f ( x ∗ ) \boldsymbol 0 \in \partial f(\boldsymbol x^*) 0∈∂f(x∗)。
证明:因为函数 f ( x ) f(\boldsymbol x) f(x)在 x ∗ \boldsymbol x^* x∗处取得最小值,所以 f ( x ) − f ( x 0 ) ≥ 0 f(\boldsymbol x)-f(\boldsymbol x_0)\ge0 f(x)−f(x0)≥0,若取 g = 0 \boldsymbol g=\boldsymbol 0 g=0,则满足次微分的定义,因此该结论成立。
2) ∂ ( α f ) = α ∂ ( f ) \partial(\alpha f)=\alpha\partial( f) ∂(αf)=α∂(f)
3) ∂ ( f + g ) = α ∂ ( f ) + α ∂ ( g ) \partial(f+g)=\alpha\partial(f)+\alpha\partial(g) ∂(f+g)=α∂(f)+α∂(g)
4) ∂ f ( A x + b ) = A T ∂ f ( x ) \partial f(\boldsymbol {Ax+b})=\boldsymbol A^T \partial f(\boldsymbol x) ∂f(Ax+b)=AT∂f(x)
二、次梯度优化算法
2.1 基本迭代公式
将梯度下降法中的梯度下降方向换为次梯度方向,即可得到次梯度迭代方法: x : = x − λ g ( x ) , g ∈ ∂ f ( x ) \boldsymbol x:=\boldsymbol x-\lambda \boldsymbol g(\boldsymbol x), \boldsymbol g\in \partial f(\boldsymbol x) x:=x−λg(x),g∈∂f(x)式中 λ \lambda λ为步长。
值的注意的是:若随意选 g \boldsymbol g g,则沿着次梯度方向前进一小步有可能使得结果变得更差(如第一部分图中的b所示),所以次梯度优化并不一定是一个下降的方法。
在实际操作中,每步迭代的最终解应当是在所有迭代方案出现过的最优解,即: f ( x b e s t k ) = min g ( f ( x ) − λ g ( x ) ) f(\boldsymbol x^k_{best})=\min_{\boldsymbol g}(f(\boldsymbol x)-\lambda g(\boldsymbol x)) f(xbestk)=gmin(f(x)−λg(x))
2.2 收敛性
如上所述,既然次梯度优化不能保证其每步一定是下降的方法,那利用其求解最优化问题有无保证?
这里不加详细推导的直接给出结论:
在函数 f f f满足Lipschitz 条件下,可以证明次梯度优化是可以收敛到最优解处的。Lipschitz 条件如下: ∣ f ( x ) − f ( y ) ∣ ≤ G ∣ ∣ x − y ∣ ∣ 2 |f(x)-f(y)|\le G||x-y||_2 ∣f(x)−f(y)∣≤G∣∣x−y∣∣2如果所需的精度为 ϵ \epsilon ϵ,其收敛速度为 O ( 1 / ϵ 2 ) O(1/\epsilon^2) O(1/ϵ2)。这说明,次梯度优化的速度很慢。
2.3 步长选择
和梯度下降法一样,其步长选择的常见策略有两种:
(1)固定步长
(2)选择不断减小的步长,但是步长也不能减少的很快,常用的一种方式是使得步长满足: ∑ k = 1 ∞ t k 2 < ∞ , ∑ k = 1 ∞ t k = ∞ \sum_{k=1}^\infin t_k^2<\infin, \qquad\sum_{k=1}^\infin t_k=\infin k=1∑∞tk2<∞,k=1∑∞tk=∞