BN算法

Motivation

2015年的论文《Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift》阐述了BN算法，这个算法目前已经被大量应用，很多论文都会引用这个算法，进行网络训练，可见其强大之处非同一般。

论文作者认为：

网络训练过程中参数不断改变导致后续每一层输入的分布也发生变化，而学习的过程又要使每一层适应输入的分布，因此我们不得不降低学习率、小心地初始化。

论文作者将分布发生变化称之为 internal covariate shift。

大家应知道，一般在训练网络的时会将输入减去均值，还有些人甚至会对输入做白化等操作，目的是为了加快训练。为什么减均值、白化可以加快训练呢，这里做一个简单地说明：

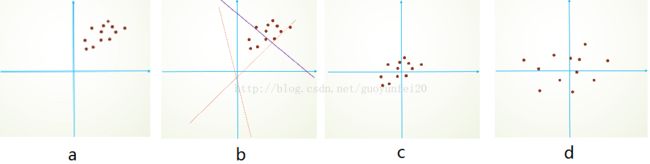
首先，图像数据是高度相关的，假设其分布如下图a所示(简化为2维)。由于初始化的时候，我们的参数一般都是0均值的，因此开始的拟合y=Wx+b，基本过原点附近，如图b红色虚线。因此，网络需要经过多次学习才能逐步达到如紫色实线的拟合，即收敛的比较慢。如果我们对输入数据先作减均值操作，如图c，显然可以加快学习。更进一步的，我们对数据再进行去相关操作，使得数据更加容易区分，这样又会加快训练，如图d。

白化的方式有好几种，常用的有PCA白化：即对数据进行PCA操作之后，在进行方差归一化。这样数据基本满足0均值、单位方差、弱相关性。作者首先考虑，对每一层数据都使用白化操作，但分析认为这是不可取的。因为白化需要计算协方差矩阵、求逆等操作，计算量很大，此外，反向传播时，白化操作不一定可导。于是，作者采用下面的Normalization方法。

在深度学习中，随机梯度下降已经成为主要的训练方法。尽管随机梯度下降法对于训练深度网络简单高效，但需要人为的选择一些参数，比如学习率、参数初始化、权重衰减系数、dropout比例等。这些参数的选择对训练结果至关重要，以至于我们很多时间都浪费在这些的调参上。那么学完这篇文献之后，你可以不需要那么刻意的慢慢调整参数。BN算法的强大之处表现在：

1. 可以选择比较大的初始学习率，让训练速度飙涨。以前需要慢慢调整学习率，甚至在网络训练到一半时，还需要想着学习率进一步调小的比例，选择多少比较合适，现在我们可以采用初始很大的学习率，然后学习率的衰减速度也很大，因为这个算法收敛很快。当然这个算法即使你选择了较小的学习率，也比以前的收敛速度快，因为它具有快速训练收敛的特性；
2. 你再也不用去理会过拟合中dropout、L2正则项参数的选择问题，采用BN算法后，你可以移除这两项了参数，或者可以选择更小的L2正则约束参数了，因为BN具有提高网络泛化能力的特性；
3. 再也不需要使用局部响应归一化层了，因为BN本身就是一个归一化网络层；
4. 可以把训练数据彻底打乱（防止每批训练的时候，某一个样本都经常被挑选到）。

大家知道，在开始训练神经网络前，都要对输入数据做一个归一化处理，那么具体为什么需要归一化呢？归一化后有什么好处呢？原因在于：

1. 神经网络学习过程本质就是为了学习数据分布，如果训练数据与测试数据的分布不同，那么网络的泛化能力也大大降低；
2. 如果每批训练数据的分布各不相同(batch 梯度下降)，那么网络就要在每次迭代都去学习适应不同的分布，这样将会大大降低网络的训练速度。

对于深度网络的训练是一个复杂的过程，只要网络的前面几层发生微小的改变，那么后面几层就会被累积放大下去。一旦网络某一层的输入数据的分布发生改变，那么这一层网络就需要去适应学习这个新的数据分布，所以如果训练过程中，训练数据的分布一直在发生变化，那么将会影响网络的训练速度。

大家知道，网络在训练的过程中，除了输入层的数据外（因为一般输入层的数据会人为的对每个样本进行归一化），后边各层的输入数据的分布一直在发生变化的。对于中间各层在训练过程中，数据分布的改变称之为 internal covariate shift。NP算法就是为了解决在训练过程中，中间层数据分布发生改变的情况下的数据归一化的。

一、BN概述

就像激活函数层、卷积层、全连接层、池化层一样，BN也属于网络的一层。前面提到网络除了输入层外，其它各层因为前层网络在训练的时候更新了参数，而引起后层输入数据分布的变化。这个时候我们可能就会想，如果在每一层输入时，再加个预处理操作，把它归一化至：均值0、方差为1，然后再输入后层计算，这样便解决了前面所提到的 Internal Covariate Shift的问题了。事实上，论文中算法本质原理就是这样：在网络的每一层输入的时候，又插入了一个归一化层，也就是先做一个归一化处理，然后再进入网络的下一层。不过文献提到的归一化层，并不像我们想象的那么简单，它是一个可学习、有参数的网络层。

二、预处理

说到神经网络输入数据预处理，最好的算法莫过于 白化预处理。然而白化计算量太大了，很不划算，还有就是白化不是处处可微的，所以在深度学习中，其实很少用到白化。经过白化预处理后，数据满足条件：

1. 特征之间的相关性降低，这个就相当于PCA（主成分分析）；
2. 数据均值、标准差归一化，也就是使得每一维特征均值为0，标准差为1。

如果数据特征维数比较大，要进行PCA，也就是实现白化的第1个要求，是需要计算特征向量，计算量非常大，于是为了简化计算，作者忽略了第1个要求，仅仅使用了下面的公式进行预处理，也就是近似白化预处理。

由于训练过程采用了 batch随机梯度下降，因此 指的是一批训练数据时，各神经元输入值的平均值； 指的是一批训练数据时各神经元输入值的标准差！

三、变换重构

看到上边的公式，大家可能会感觉很简单。就是对中间层的输入数据归一化嘛！其实没那么简单，比如网络中间层的数据的真实分布是一个Sigmoid分布，按上式强制归一化处理后，势必会破坏此分布！为了解决这个问题，论文提出了： 变换重构的概念！引入了可学习的参数γ、β，这才是BN算法关键之处：

每一个神经元都会有一对这样的参数γ、β。这样其实当：

时，是可以恢复出原始的某一层所学到的特征的。引入可学习重构参数γ、β，让网络可以学习恢复出原始网络所要学习的特征分布。

四、BN实现

BN层的前向传导过程公式为：

五、思考1

网络一旦训练完成；所以的参数都是固定不变的了；因此一个网络在预测时，测试样本经过中间各层时，用到的是训练好的μ、β来进行归一化处理！所以，预测阶段BN的公式为：

上式的简单理解为：对于均值，直接计算batch的平均值；然后对标准差采用batch的无偏估计。最后：

六、思考2

文献主要是把BN变换，置于网络激活函数层的前面。在没有采用BN的时候，激活函数层是这样的：

z = g(Wx + b)

增加BN后，是这样的：

z = g( BN(Wx + b) )

其实，因为偏置参数b经过BN层后是没有用的，最后也会被均值归一化。另一方面，BN层后面还有个β参数作为偏置项，所以b这个参数就可以不用了。因此最后把BN层+激活函数层就变成了：

z = g( BN(Wx) )

七、BN在CNN中的使用

通过上面的学习，我们知道BN层是对于每个神经元做归一化处理，甚至只需要对某一个神经元进行归一化，而不是对一整层网络的神经元进行归一化。

既然BN是对单个神经元的运算，那么在CNN中卷积层上要怎么办？假如某一层卷积层有6个特征图，每个特征图的大小是100*100，这样就相当于这一层网络有6*100*100个神经元，如果采用BN，就会有6*100*100个参数γ、β，这样岂不是太恐怖了。因此卷积层上的BN使用，其实也是使用了类似权值共享的策略，把一整张特征图当做一个神经元进行处理。

说白了，这就是相当于求取所有样本所对应的一个特征图的所有神经元的平均值、方差，然后对这个特征图神经元做归一化。下面是TensorFlow在mnist数据集分类的举例:

# coding=UTF-8
# neural network structure for this sample:
#
# · · · · · · · · · ·   (input data, 1-deep)                     X [batch, 28, 28,  1]
# @ @ @ @ @ @ @ @ @ @   conv. layer +BN  5x5x1=> 24 stride 1    W1 [    5,  5,  1, 24]  B1 [24]
#                                                               Y1 [batch, 28, 28,  6]
#   @ @ @ @ @ @ @ @     conv. layer +BN  5x5x6=> 48 stride 2    W2 [    5,  5,  6, 48]  B2 [48]
#                                                               Y2 [batch, 14, 14, 12]
#     @ @ @ @ @ @       conv. layer +BN 4x4x12=> 64 stride 2    W3 [    4,  4, 12, 64]  B3 [64]
#                                                               Y3 [batch,  7,  7, 24] 
#                                                => reshaped to YY [batch, 7*7*24]
#      \x/x\x\x/        fully connected layer (relu+dropout+BN) W4 [7*7*24, 200]        B4 [200]
#       · · · ·                                                 Y4 [batch,  200]
#       \x/x\x/         fully connected layer (softmax)         W5 [200,     10]        B5 [10]
#        · · ·                                                   Y [batch,   10]

import tensorflow as tf
import math
from tensorflow.examples.tutorials.mnist import input_data as mnist_data
tf.set_random_seed(0.0)

# Download images and labels into mnist.test (10K images+labels) 
# and mnist.train (60K images+labels)
mnist = mnist_data.read_data_sets("data", one_hot=True, reshape=False, validation_size=0)

# Ylogits      - input data that need tobe batch normalised. For convolutional
#                layer, it's a 4-D tensor. For fully connected layer, it's a 2-D tensor
# is_test      - flag, is_test = False for train
#                      is_test = True  for test
# offset       - beta
#                gamma(scaling) is not useful for relu 
def batchnormForRelu(Ylogits, is_test, Iteration, offset, convolutional=False):
    # adding the iteration prevents from averaging across non-existing iterations
    exp_moving_avg = tf.train.ExponentialMovingAverage(0.999, Iteration) 
    bnepsilon = 1e-5
    if convolutional:
        mean, variance = tf.nn.moments(Ylogits, [0, 1, 2])
    else:
        mean, variance = tf.nn.moments(Ylogits, [0])
    update_moving_averages = exp_moving_avg.apply([mean, variance])
    m = tf.cond(is_test, lambda: exp_moving_avg.average(mean), lambda: mean)
    v = tf.cond(is_test, lambda: exp_moving_avg.average(variance), lambda: variance)
    Ybn = tf.nn.batch_normalization(Ylogits, m, v, offset, None, bnepsilon)
    return Ybn, update_moving_averages

def compatible_convolutional_noise_shape(Y):
    noiseshape = tf.shape(Y)
    noiseshape = noiseshape * tf.constant([1,0,0,1]) + tf.constant([0,1,1,0])
    return noiseshape

# input X: 28x28 grayscale images
X  = tf.placeholder(tf.float32, [None, 28, 28, 1])
# correct answers will go here
Y_ = tf.placeholder(tf.float32, [None, 10])
# variable learning rate
lr = tf.placeholder(tf.float32)
# test flag for batch norm
tst = tf.placeholder(tf.bool)
Iter = tf.placeholder(tf.int32)
# dropout probability
pkeep = tf.placeholder(tf.float32)
pkeep_conv = tf.placeholder(tf.float32)

# three convolutional layers with their channel counts, and a
# fully connected layer (tha last layer has 10 softmax neurons)
K = 24  # 1st convolutional layer output depth
L = 48  # 2nd convolutional layer output depth
M = 64  # 3rd convolutional layer
N = 200 # 4th fully connected layer

W1 = tf.Variable(tf.truncated_normal([6, 6, 1, K], stddev=0.1))  # 6x6 patch, 1 input channel, K output channels
B1 = tf.Variable(tf.constant(0.1, tf.float32, [K]))
W2 = tf.Variable(tf.truncated_normal([5, 5, K, L], stddev=0.1))
B2 = tf.Variable(tf.constant(0.1, tf.float32, [L]))
W3 = tf.Variable(tf.truncated_normal([4, 4, L, M], stddev=0.1))
B3 = tf.Variable(tf.constant(0.1, tf.float32, [M]))

W4 = tf.Variable(tf.truncated_normal([7 * 7 * M, N], stddev=0.1))
B4 = tf.Variable(tf.constant(0.1, tf.float32, [N]))
W5 = tf.Variable(tf.truncated_normal([N, 10], stddev=0.1))
B5 = tf.Variable(tf.constant(0.1, tf.float32, [10]))

# The model
# batch norm scaling is not useful with relus
# batch norm offsets are used instead of biases
Y1l = tf.nn.conv2d(X, W1, strides=[1, 1, 1, 1], padding='SAME')
Y1bn, update_ema1 = batchnormForRelu(Y1l, tst, Iter, B1, convolutional=True)
Y1r = tf.nn.relu(Y1bn)
Y1 = tf.nn.dropout(Y1r, pkeep_conv, compatible_convolutional_noise_shape(Y1r))
stride = 2  # output is 14x14
Y2l = tf.nn.conv2d(Y1, W2, strides=[1, stride, stride, 1], padding='SAME')
Y2bn, update_ema2 = batchnormForRelu(Y2l, tst, Iter, B2, convolutional=True)
Y2r = tf.nn.relu(Y2bn)
Y2 = tf.nn.dropout(Y2r, pkeep_conv, compatible_convolutional_noise_shape(Y2r))
stride = 2  # output is 7x7
Y3l = tf.nn.conv2d(Y2, W3, strides=[1, stride, stride, 1], padding='SAME')
Y3bn, update_ema3 = batchnormForRelu(Y3l, tst, Iter, B3, convolutional=True)
Y3r = tf.nn.relu(Y3bn)
Y3 = tf.nn.dropout(Y3r, pkeep_conv, compatible_convolutional_noise_shape(Y3r))
# reshape
YY = tf.reshape(Y3, shape=[-1, 7 * 7 * M])
Y4l = tf.matmul(YY, W4)
Y4bn, update_ema4 = batchnormForRelu(Y4l, tst, Iter, B4)
Y4r = tf.nn.relu(Y4bn)
Y4 = tf.nn.dropout(Y4r, pkeep)
Ylogits = tf.matmul(Y4, W5) + B5
Y = tf.nn.softmax(Ylogits)

update_ema = tf.group(update_ema1, update_ema2, update_ema3, update_ema4)

# cross-entropy loss function (= -sum(Y_i * log(Yi)) ), normalised for batches of 100  images
# TensorFlow provides the softmax_cross_entropy_with_logits function to avoid numerical stability
# problems with log(0) which is NaN
cross_entropy = tf.nn.softmax_cross_entropy_with_logits(logits=Ylogits, labels=Y_)
cross_entropy = tf.reduce_mean(cross_entropy)*100

# accuracy of the trained model, between 0 (worst) and 1 (best)
correct_prediction = tf.equal(tf.argmax(Y, 1), tf.argmax(Y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

# training step, the learning rate is a placeholder
train_step = tf.train.AdamOptimizer(lr).minimize(cross_entropy)

# init
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)

def training_step(i, update_test_data, update_train_data):

    # training on batches of 100 images with 100 labels
    batch_X, batch_Y = mnist.train.next_batch(100)

    # learning rate decay
    max_learning_rate = 0.02
    min_learning_rate = 0.0001
    decay_speed = 1600
    learning_rate = min_learning_rate + (max_learning_rate - min_learning_rate) * math.exp(-i/decay_speed)

    # compute training values for visualisation
    if update_train_data:
        a, c = sess.run([accuracy, cross_entropy], \
        {X: batch_X, Y_: batch_Y, tst: False, pkeep: 1.0, pkeep_conv: 1.0})
        print(str(i) + ": accuracy:" + str(a) + " loss: " + str(c) + " (lr:" + str(learning_rate) + ")")
    # compute test values for visualisation
    if update_test_data:
        a, c = sess.run([accuracy, cross_entropy], \
        {X: mnist.test.images, Y_: mnist.test.labels, tst: True, pkeep: 1.0, pkeep_conv: 1.0})
        print(str(i) + ": ********* epoch " + str(i*100//mnist.train.images.shape[0]+1) + " ********* test accuracy:" + str(a) + " test loss: " + str(c))
    # the backpropagation training step
    sess.run(train_step, {X: batch_X, Y_: batch_Y, lr: learning_rate, tst: False, pkeep: 0.75, pkeep_conv: 1.0})
    sess.run(update_ema, {X: batch_X, Y_: batch_Y, tst: False, Iter: i, pkeep: 1.0, pkeep_conv: 1.0})

if __name__ == "__main__":
    for i in range(0, 1000):
       training_step(i, True, True)