神经网络改进算法
《Neural Networks and Deep Learning》学习笔记——《Neural Networks and Deep Learning》是Michael Nielsen 所著的一本神经网络与深度学习的在线学习教材,通过Python(+Theano)实现神经网络识别MNIST手写数据集,生动易懂的讲解了神经网络与深度学习的基本原理,是一本非常不错的入门教材。本文是对其学习的总结。
目录
- 初识神经网络
1.1 感知器
1.2 Sigmoid函数
1.3 代价函数
1.4 梯度下降算法 - 反向传播算法
- 神经网络改进算法
3.1Cross-entropy代价函数——神经元饱和
3.2正则化(Regularization)——过拟合
3.3权值初始化——隐含层神经元饱和 - 深度学习
4.1 万有逼近定理(Universal Approximation Theory)
4.2 训练深度神经网络时的问题
4.3 卷积神经网络(CNN)
1.Cross-entropy代价函数
首先让我们回顾一下Sigmoid函数:

从图中可以直观的看出Sigmoid函数两端区域“平坦”,即当z很大或很小时其导数 σ′(z)→0 σ ′ ( z ) → 0 。那么这会引起什么问题呢?
以两层神经网络(输入-输出)为例,当代价函数C为二次代价函数时,有
当 σ′(z)→0 σ ′ ( z ) → 0 时,梯度值会变得很小,也就是说我们的神经网络会学习得很慢,这种现象被称为神经元饱和(Neuron Saturation)。
针对这一问题,引入Cross-entropy代价函数:
很明显它满足作为代价函数的两个性质:(1)C>0,(2)当 a≈y a ≈ y 时, C≈0 C ≈ 0
对其求梯度,得:
从上面式(4)(5)可以看出,梯度中没有了 σ′(z) σ ′ ( z ) 项,因此Cross-entropy代价函数避免了神经元饱和问题。并且初始输出a与理想输出y偏差越大,学习速率越快(类似于人类从错误中快速学习经验)。
下面再介绍一种输出层激活函数——Softmax激活函数:
容易证明Softmax层的所有输出和为1,且都为正数。因此Softmax层的输出可以看做是概率分布。基于这种性质,Softmax函数很适合用于输出层,即输出神经网络估计的正确输出的概率。
与Softmax相对应的代价函数是Log-likelihood代价函数:
其梯度为:
因此Softmax激活函数和Log-likelihood代价函数的组合同样也可以避免神经元饱和的问题。
避免神经元饱和现象的函数组合:
| 激活函数 | 代价函数 |
|---|---|
| Linear | Quadratic |
| Sigmoid | Cross-entropy |
| Softmax | Log-likelihood |
2.正则化(Regularization)
在训练神经网络的时候,除了会遇到神经元饱和问题,还会遇到过拟合(Overfitting)问题。
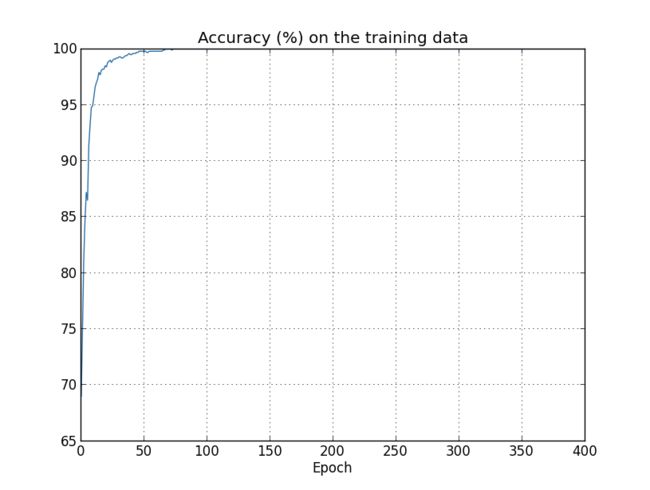
当设置的参数远大于实际需要的参数时就会出现过拟合问题,表现为训练样本输出正确率增加,而测试样本的输出正确率却趋于平稳,而且其输出正确率远低于训练样本输出正确率。如下图所示,
训练样本代价函数:
训练样本输出正确率:
测试样本代价函数:
测试样本输出正确率:
![]()
这种现象就好像我们的神经网络对训练样本集有很好的“记忆”,却对新的测试样本集没有很好的“归纳推广”。
对于过拟合问题我们可以简单的运用交叉验证(hold-out方法)和通过实时追踪学习效果的提前停止训练的方法来减少过拟合。(增加训练样本或减小神经网络尺寸也可以减少过拟合,但在实际应用中却不适用)
正则化方法是一个能有效减少过拟合问题的手段。下面以L2正则化为例介绍正则化,对于正则化的代价函数有:
其中 C0 C 0 为代价函数, λ2n∑ww2 λ 2 n ∑ w w 2 称为正则项, λ λ 称为正则系数。
对其求梯度,得:
则学习的权值和偏置分别为:
从式(13)可以看出,因为系数 1−ηλn 1 − η λ n 的存在,使得 ω ω 变得更小,因此L2正则化又被称为权值衰退,基于此当加入正则项后,在代价函数减小的同时,神经网络更偏向于学习小的权值。
小的权值就意味着当输入发生一些扰动时,我们的神经网络不会受太大影响,即学习的是在样本集中经常出现的模式(Pattern),而不会受局部扰动(噪声)太大的影响。
除了L2正则化还有其他几种正则化方法:
(1)L1正则化:
易得,
应用了L1正则化的网络学习主要聚焦于很小一部分的但十分重要的节点( ω ω 较大),其他节点( ω ω 较小)的权值将趋于0。
(2)Dropout:
不同于L1,L2正则化,Dropout不对代价函数做任何修正。其思想是:
假设(临时地)随机断开隐含层一半神经元与输入输出层的连接
神经网络具体执行流程不变,在得到了一组小批量(mini-batch)样本梯度(随机梯度下降法),更新权值和偏置后,恢复之前的隐含层神经元连接,重新随机选取另一组神经元重复上面Dropout操作(断开连接)
,重复前述过程直到获得目标输出。
不同的神经网络会出现不同方式的过拟合问题,Dropout相当于训练不同的神经网络,然后对这些不同的过拟合做平均来减少过拟合。因此Dropout适用于大型深度神经网络。
(3)训练样本扩展:
前面我们提到过增加训练样本数可以减少过拟合问题,但实际应用中大量的训练样本集并不容易获得。因此我们可以手动扩展训练样本。例如,对图片样本进行旋转,对语音样本添加背景噪声……
3.权值初始化
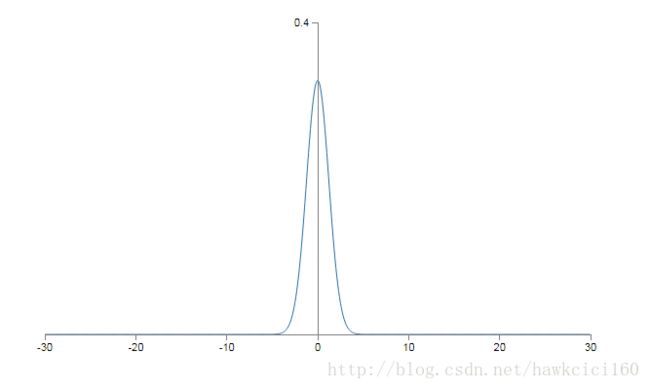
假设我们应用标准高斯随机分布来初始化权值和偏置。设有1000个输入,一半为0,另一半为1。易得其加权输入 z=∑jwjxj+b z = ∑ j w j x j + b 的标准差为 501−−−√≈22.4 501 ≈ 22.4 。则z的高斯分布为:
![]()
由上图z的分布可以得知|z|的值可能会很大,因此隐含层神经元的输出就会出现饱和,降低学习速率。
因为前面介绍的Cross-entropy代价函数针对的是输出层的饱和,所以对隐含层并不适用。
现在让我们应用均值为0,标准差为 1/nin−−−√ 1 / n i n 的高斯分布对权值进行初始化。易得,z的标准差为 3/2−−−√=1.22… 3 / 2 = 1.22 … ,z的分布如下图所示:
由上图可知|z|会集中在一个很小的范围内,因此降低了发生神经元饱和问题的概率。
PS:参数初始化方法的选择和激活函数有关
总结:在实际训练神经网络时,会遇到两个主要问题神经元饱和或过拟合:
| 问题 | 方法 |
|---|---|
| 输出层神经元饱和 | Cross-entropy代价函数 |
| 隐含层神经元饱和 | 权值初始化 |
| 过拟合 | 正则化 |
附录:
各优化方法比较图(图片来源 https://twitter.com/alecrad)
“Notice that momentum-based methods, Momentum and Nesterov accelerated gradient descent (NAG), tend to overshoot the optimal path by “rolling downhill” too fast, whereas standard SGD moves in the right path, but too slowly. Adaptive methods – AdaGrad, AdaDelta, and RMSProp (and we could add Adam to it as well) – tend to have the per-parameter flexibility to avoid both of those trappings.”
“So which optimization method works best? There’s no simple answer to this, and the answer largely depends on the characteristics of your data and other training constraints and considerations. Nevertheless, Adam has emerged as a promising method to at least start with.”
推荐阅读:
https://ml4a.github.io/ml4a/how_neural_networks_are_trained/
http://ruder.io/optimizing-gradient-descent/index.html