一、基于度量分析自己的程序结构
(一)第一次作业
第一次作业是实现简单的多项式求导,主要是针对幂函数和常数,二者结合成因子,因子相加减为项,由项构成表达式。
总体上采用了状态机,使用状态机前,先利用正则表达式匹配分析并去掉了合法的空格。采用状态机的好处是很明显的,对于输入处理这一块绝对没有问题了,可以很方便的进行判断。不过我有一个致命的错误就是用了状态机却没有去掉正则表达式匹配,而正则又存在错误,导致有些有效输入被判断为“WRONG FORMAT”。状态机图示如下:
(当然对于输入处理还可以采用正则表达式匹配,逐项匹配不再回退,对于本次作业也会有不错的效果)
状态机在分析到合法的一项时调用item类中的求导函数进行相应处理,求导结果通过toString保存到输出的字符串里,再进一步化简,最后输出结果。对于化简这一部分我做的并不好,实现的只有简单的符号合并,值为0,系数指数为1的项的最基本化简。而对于同类项合并等,并没有完成。理论上经过求导,可以对得到的字符串进行再处理,得到每一项的系数指数,再进行合并。遗憾的是,由于java编程不熟练和作业拖沓,这一项并没有完成。
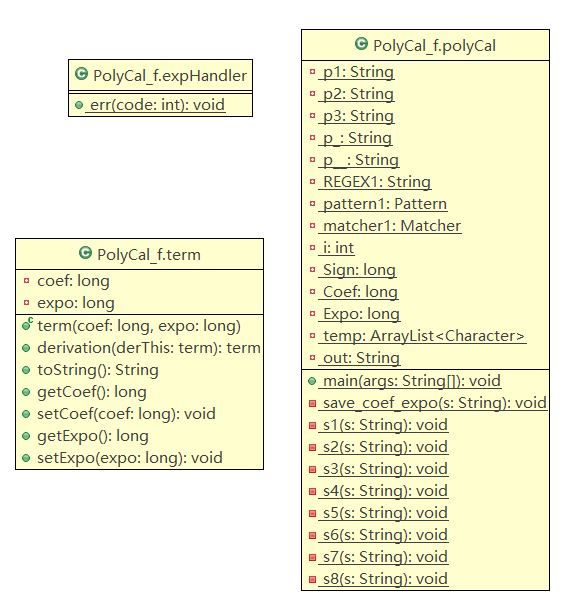
第一次作业的类图如下:
可以看出,类之间没有耦合,完全没有面向对象,Java版过程实现……
(二)第二次作业
第二次作业的基础上加入了三角函数sin(x)和cos(x),三角函数可以有系数指数。
第二次作业采用了递归下降法,总体与第一次作业类似,只是重新建立了因子类,各个具体的因子类继承Factor类,针对幂函数因子、三角函数因子、常数因子分别实现求导,最后将求导结果合并进行简单化简。
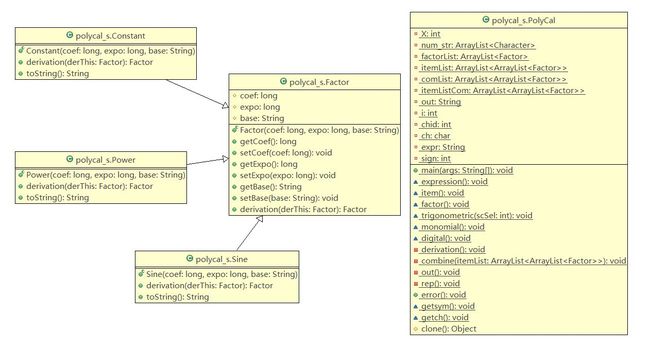
第二次作业的类图如下:
可以看出类之间的继承关系。然而PolyCal类还是很庞大,充当了主函数的作用……
(三)第三次作业
第三次作业在第二次作业的基础上改变了因子,因子可以是一个带括号的表达式。
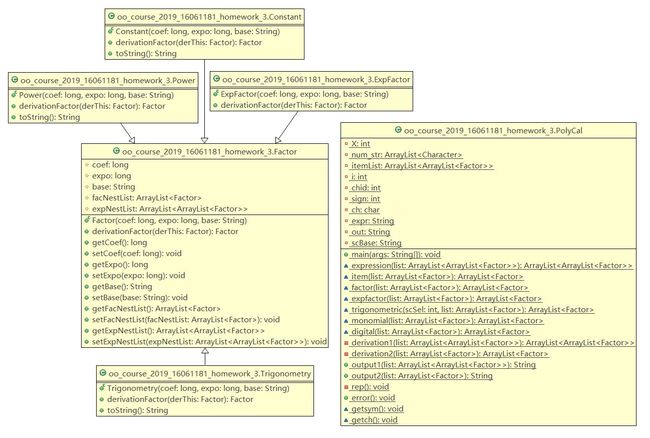
第三次作业,延用了递归下降分析法。因为存在嵌套求导的关系,所以在存储因子时,我将嵌套的表达式因子作为底(Base)存了下来,类型依然是一个ArrayList,求导时,也方便进行嵌套求导。缺点在于求导结束输出时不大方便,我没有实现简单的输出。
老问题,PolyCal类……面向对象与我而言实现起来还是很抽象……
总结一下,采用递归下降法,其可扩展性显而易见的优秀。
二、分析自己程序的bug
(一)第一次作业
第一次作业比较简单,不过也翻了车。错误很明显,在运用状态机的同时采用了正则表达式完全匹配表达式,而且我还 “if(in.matches()){ …… } else{ error(); }” 了(脑残忘了删),因此强测就……崩;还有一点就是没有进行字符串再处理从而充分的化简。
(二)第二次作业
第二次作业的bug主要存在于求导后的输出。输出时时常会有字符乱入,各个因子类的toString()方法都有问题,根本在于逻辑分析的问题,在设计时条件判断不准确,连带了其他不该出现的输出。
另外,在状态机处理时,对于每一项的首部如 “-sin(x)”, “-x” 等,没有记录下其符号,最后输出时全部处理为了 “+” ,看到最后结果里的 “+”,只想伸手来一巴掌把那一竖打掉……
(三)第三次作业
第三次作业的问题在于嵌套的ArrayList的输出 。因子的底(Base)可以是一个因子(表达式因子),所以底也是一个ArrayList,如果这个表达式因子里又是一个底为表达式的因子(即嵌套),会导致ArrayList(ArrayList(ArrayList……)),求导也实现了嵌套求导,问题在于输出求导结果的时候比较容易出错(而我也的确出了错),没有实现较为简易的输出整合方式。也许可以在求导时就进行记录以便处理输出。
最后坦诚一点,最大的bug是作业提交之前没有进行充分自测试。
三、分析自己发现别人程序bug所采用的的策略
太菜了没有进入互测,丢掉这个学习机会很难过...
在自我测试中,情况如下:
1. 关于第一个因子引起的符号问题。
++++…+显然是不正确的输入,但是+++x,+++1的情况另当别论,+++x很不幸还是错误的,但+++1是正确的。因为+++1可以表示为 +1+ +1的简写。算是一个需要注意的点;
2. 老生常谈的使用正则表达式匹配输入可能引起的爆栈问题。
3. 对于中间因子带符号的符号判断与处理,诸如 x+ -sin(x) 等。
4. 嵌套因子求导的正确性问题。
没有实现自动的测试,手动输入较为特殊的用例肝……
四、Applying Creational Pattern
结合以上三次作业,问题很明显,在ddl前不见得可以完全拎得清程序逻辑,而且就算拎得清了也不见得有能力尽快实现,导致最后有漏洞百出的程序成品和并未进行完的测试以及没有通过的测试点。
不过对于这几次作业,递归下降是真的好用啊,可扩展性很强。所以在作业完善方面,主要还是重写具体因子类的toString()方法,输出字符串的整合处理需要修正,输出字符串的化简需要完善(sin(X)^2 + cos(X)^2 = 1等公式(和差化积、二倍角等), 同类项合并)。