机器学习之svm---车牌识别

目标

团队 承接嵌入式linux软硬件开发、机器视觉 图像处理、网络流等项目

微信号：hgz1173136060

本文档尝试解答如下问题:

• 如何使用OpenCV函数 CvSVM::train 训练一个SVM分类器， 以及用 CvSVM::predict 测试训练结果。

一、简单介绍与opencv的使用

什么是支持向量机(SVM)?

支持向量机 (SVM) 是一个类分类器，正式的定义是一个能够将不同类样本在样本空间分隔的超平面。 换句话说，给定一些标记(label)好的训练样本 (监督式学习), SVM算法输出一个最优化的分隔超平面。

如何来界定一个超平面是不是最优的呢? 考虑如下问题：

假设给定一些分属于两类的2维点，这些点可以通过直线分割， 我们要找到一条最优的分割线.

Note

 

在这个示例中，我们考虑卡迪尔平面内的点与线，而不是高维的向量与超平面。 这一简化是为了让我们以更加直觉的方式建立起对SVM概念的理解， 但是其基本的原理同样适用于更高维的样本分类情形。

在上面的图中， 你可以直觉的观察到有多种可能的直线可以将样本分开。 那是不是某条直线比其他的更加合适呢? 我们可以凭直觉来定义一条评价直线好坏的标准:

距离样本太近的直线不是最优的，因为这样的直线对噪声敏感度高，泛化性较差。 因此我们的目标是找到一条直线，离所有点的距离最远。

由此， SVM算法的实质是找出一个能够将某个值最大化的超平面，这个值就是超平面离所有训练样本的最小距离。这个最小距离用SVM术语来说叫做 间隔(margin) 。 概括一下，最优分割超平面 最大化 训练数据的间隔。

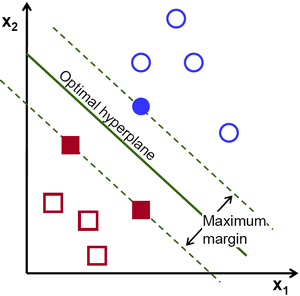
如何计算最优超平面?

下面的公式定义了超平面的表达式:

 叫做 权重向量 ，  叫做 偏置(bias) 。

See also

 

关于超平面的更加详细的说明可以参考T. Hastie, R. Tibshirani 和 J. H. Friedman的书籍 Elements of Statistical Learning ， section 4.5 (Seperating Hyperplanes)。

最优超平面可以有无数种表达方式，即通过任意的缩放  和  。 习惯上我们使用以下方式来表达最优超平面

式中  表示离超平面最近的那些点。 这些点被称为 支持向量**。 该超平面也称为 **canonical 超平面.

通过几何学的知识，我们知道点  到超平面  的距离为:

特别的，对于 canonical 超平面, 表达式中的分子为1，因此支持向量到canonical 超平面的距离是

刚才我们介绍了间隔(margin),这里表示为 , 它的取值是最近距离的2倍:

最后最大化  转化为在附加限制条件下最小化函数  。 限制条件隐含超平面将所有训练样本  正确分类的条件,

式中  表示样本的类别标记。

这是一个拉格朗日优化问题，可以通过拉格朗日乘数法得到最优超平面的权重向量  和偏置  。

源码

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68

#include #include #include using namespace cv; int main() { // Data for visual representation int width = 512, height = 512; Mat image = Mat::zeros(height, width, CV_8UC3); // Set up training data float labels[4] = {1.0, -1.0, -1.0, -1.0}; Mat labelsMat(3, 1, CV_32FC1, labels); float trainingData[4][2] = { {501, 10}, {255, 10}, {501, 255}, {10, 501} }; Mat trainingDataMat(3, 2, CV_32FC1, trainingData); // Set up SVM's parameters CvSVMParams params; params.svm_type = CvSVM::C_SVC; params.kernel_type = CvSVM::LINEAR; params.term_crit = cvTermCriteria(CV_TERMCRIT_ITER, 100, 1e-6); // Train the SVM CvSVM SVM; SVM.train(trainingDataMat, labelsMat, Mat(), Mat(), params); Vec3b green(0,255,0), blue (255,0,0); // Show the decision regions given by the SVM for (int i = 0; i < image.rows; ++i) for (int j = 0; j < image.cols; ++j) { Mat sampleMat = (Mat_<float>(1,2) << i,j); float response = SVM.predict(sampleMat); if (response == 1) image.at<Vec3b>(j, i) = green; else if (response == -1) image.at<Vec3b>(j, i) = blue; } // Show the training data int thickness = -1; int lineType = 8; circle( image, Point(501, 10), 5, Scalar( 0, 0, 0), thickness, lineType); circle( image, Point(255, 10), 5, Scalar(255, 255, 255), thickness, lineType); circle( image, Point(501, 255), 5, Scalar(255, 255, 255), thickness, lineType); circle( image, Point( 10, 501), 5, Scalar(255, 255, 255), thickness, lineType); // Show support vectors thickness = 2; lineType = 8; int c = SVM.get_support_vector_count(); for (int i = 0; i < c; ++i) { const float* v = SVM.get_support_vector(i); circle( image, Point( (int) v[0], (int) v[1]), 6, Scalar(128, 128, 128), thickness, lineType); } imwrite("result.png", image); // save the image imshow("SVM Simple Example", image); // show it to the user waitKey(0); }

解释

1. 建立训练样本

本例中的训练样本由分属于两个类别的2维点组成， 其中一类包含一个样本点，另一类包含三个点。

float labels[4] = {1.0, -1.0, -1.0, -1.0};
float trainingData[4][2] = {{501, 10}, {255, 10}, {501, 255}, {10, 501}};

函数 CvSVM::train 要求训练数据储存于float类型的 Mat 结构中， 因此我们定义了以下矩阵:

Mat trainingDataMat(3, 2, CV_32FC1, trainingData);
Mat labelsMat      (3, 1, CV_32FC1, labels);

2. 设置SVM参数

   此教程中，我们以可线性分割的分属两类的训练样本简单讲解了SVM的基本原理。 然而，SVM的实际应用情形可能复杂得多 (比如非线性分割数据问题，SVM核函数的选择问题等等)。 总而言之，我们需要在训练之前对SVM做一些参数设定。 这些参数保存在类 CvSVMParams 中。

   CvSVMParams params;
   params.svm_type    = CvSVM::C_SVC;
   params.kernel_type = CvSVM::LINEAR;
   params.term_crit   = cvTermCriteria(CV_TERMCRIT_ITER, 100, 1e-6);
   

   • SVM类型. 这里我们选择了 CvSVM::C_SVC 类型，该类型可以用于n-类分类问题 (n  2)。 这个参数定义在 CvSVMParams.svm_type 属性中.

     Note

      

     CvSVM::C_SVC 类型的重要特征是它可以处理非完美分类的问题 (及训练数据不可以完全的线性分割)。在本例中这一特征的意义并不大，因为我们的数据是可以线性分割的，我们这里选择它是因为它是最常被使用的SVM类型。

   • SVM 核类型. 我们没有讨论核函数，因为对于本例的样本，核函数的讨论没有必要。然而，有必要简单说一下核函数背后的主要思想， 核函数的目的是为了将训练样本映射到更有利于可线性分割的样本集。 映射的结果是增加了样本向量的维度，这一过程通过核函数完成。 此处我们选择的核函数类型是 CvSVM::LINEAR 表示不需要进行映射。 该参数由 CvSVMParams.kernel_type 属性定义。

   • 算法终止条件. SVM训练的过程就是一个通过 迭代 方式解决约束条件下的二次优化问题，这里我们指定一个最大迭代次数和容许误差，以允许算法在适当的条件下停止计算。 该参数定义在 cvTermCriteria 结构中。

3. 训练支持向量机

   调用函数 CvSVM::train 来建立SVM模型。

   CvSVM SVM;
   SVM.train(trainingDataMat, labelsMat, Mat(), Mat(), params);
   

4. SVM区域分割

函数 CvSVM::predict 通过重建训练完毕的支持向量机来将输入的样本分类。 本例中我们通过该函数给向量空间着色， 及将图像中的每个像素当作卡迪尔平面上的一点，每一点的着色取决于SVM对该点的分类类别：绿色表示标记为1的点，蓝色表示标记为-1的点。

Vec3b green(0,255,0), blue (255,0,0);

for (int i = 0; i < image.rows; ++i)
    for (int j = 0; j < image.cols; ++j)
    {
    Mat sampleMat = (Mat_<float>(1,2) << i,j);
    float response = SVM.predict(sampleMat);

    if (response == 1)
       image.at<Vec3b>(j, i)  = green;
    else
    if (response == -1)
       image.at<Vec3b>(j, i)  = blue;
    }

5. 支持向量

   这里用了几个函数来获取支持向量的信息。 函数 CvSVM::get_support_vector_count 输出支持向量的数量，函数 CvSVM::get_support_vector 根据输入支持向量的索引来获取指定位置的支持向量。 通过这一方法我们找到训练样本的支持向量并突出显示它们。

   int c     = SVM.get_support_vector_count();
   
   for (int i = 0; i < c; ++i)
   {
   const float* v = SVM.get_support_vector(i); // get and then highlight with grayscale
   circle(   image,  Point( (int) v[0], (int) v[1]),   6,  Scalar(128, 128, 128), thickness, lineType);
   }
   

结果

• 程序创建了一张图像，在其中显示了训练样本，其中一个类显示为白色圆圈，另一个类显示为黑色圆圈。
• 训练得到SVM，并将图像的每一个像素分类。 分类的结果将图像分为蓝绿两部分，中间线就是最优分割超平面。
• 最后支持向量通过灰色边框加重显示。

转载自： http://www.opencv.org.cn/opencvdoc/2.3.2/html/doc/tutorials/ml/introduction_to_svm/introduction_to_svm.html

点到平面的距离

点到线的距离

平行线之间的距离

超平面

二、原理与推导

转自： http://blog.csdn.net/v_july_v/article/details/7624837


前言

    动笔写这个支持向量机(support vector machine)是费了不少劲和困难的，原因很简单，一者这个东西本身就并不好懂，要深入学习和研究下去需花费不少时间和精力，二者这个东西也不好讲清楚，尽管网上已经有朋友写得不错了(见文末参考链接)，但在描述数学公式的时候还是显得不够。得益于同学白石的数学证明，我还是想尝试写一下，希望本文在兼顾通俗易懂的基础上，真真正正能足以成为一篇完整概括和介绍支持向量机的导论性的文章。

    本文在写的过程中，参考了不少资料，包括《支持向量机导论》、《统计学习方法》及网友pluskid的支持向量机系列等等，于此，还是一篇学习笔记，只是加入了自己的理解和总结，有任何不妥之处，还望海涵。全文宏观上整体认识支持向量机的概念和用处，微观上深究部分定理的来龙去脉，证明及原理细节，力保逻辑清晰 & 通俗易懂。

    同时，阅读本文时建议大家尽量使用chrome等浏览器，如此公式才能更好的显示，再者，阅读时可拿张纸和笔出来，把本文所有定理.公式都亲自推导一遍或者直接打印下来（可直接打印网页版或本文文末附的PDF，享受随时随地思考、演算的极致快感），在文稿上演算。

    Ok，还是那句原话，有任何问题，欢迎任何人随时不吝指正 & 赐教，感谢。

第一层、了解SVM

   支持向量机，因其英文名为support vector machine，故一般简称SVM，通俗来讲，它是一种二类分类模型，其基本模型定义为特征空间上的间隔最大的线性分类器，其学习策略便是间隔最大化，最终可转化为一个凸二次规划问题的求解。

1.1、分类标准的起源：Logistic回归

   理解SVM，咱们必须先弄清楚一个概念：线性分类器。

    给定一些数据点，它们分别属于两个不同的类，现在要找到一个线性分类器把这些数据分成两类。如果用x表示数据点，用y表示类别（y可以取1或者-1，分别代表两个不同的类），一个线性分类器的学习目标便是要在n维的数据空间中找到一个超平面（hyper plane），这个超平面的方程可以表示为（ wT中的T代表转置）：

                                                           

    可能有读者对类别取1或-1有疑问，事实上，这个1或-1的分类标准起源于logistic回归。

    Logistic回归目的是从特征学习出一个0/1分类模型，而这个模型是将特性的线

性组合作为自变量，由于自变量的取值范围是负无穷到正无穷。因此，使用

logistic函数（或称作sigmoid函数）将自变量映射到(0,1)上，映射后的值被认为

是属于y=1的概率。

   假设函数

   其中x是n维特征向量，函数g就是logistic函数。
    而的图像是

    可以看到，将无穷映射到了(0,1)。

    而假设函数就是特征属于y=1的概率。

   从而，当我们要判别一个新来的特征属于哪个类时，只需求即可，若大于0.5就是y=1的类，反之属于y=0类。

    此外，只和有关，>0，那么，而g(z)只是用来映射，真实的类别决定权还是在于。再者，当时，=1，反之=0。如果我们只从出发，希望模型达到的目标就是让训练数据中y=1的特征，而是y=0的特征。Logistic回归就是要学习得到，使得正例的特征远大于0，负例的特征远小于0，而且要在全部训练实例上达到这个目标。

    接下来，尝试把logistic回归做个变形。首先，将使用的结果标签y = 0和y = 1替换为y = -1,y = 1，然后将（）中的替换为b，最后将后面的替换为（即）。如此，则有了

。

也就是说除了y由y=0变为y=-1外，线性分类函数跟logistic回归的形式化表示没区别。

    进一步，可以将假设函数中的g(z)做一个简化，将其简单映射到y=-1和y=1上。映射关系如下：

1.2、线性分类的一个例子

    下面举个简单的例子，如下图所示，现在有一个二维平面，平面上有两种不同的数据，分别用圈和叉表示。由于这些数据是线性可分的，所以可以用一条直线将这两类数据分开，这条直线就相当于一个超平面，超平面一边的数据点所对应的y全是 -1 ，另一边所对应的y全是1。

    这个超平面可以用分类函数表示，当f(x) 等于0的时候，x便是位于超平面上的点，而f(x)大于0的点对应 y=1 的数据点，f(x)小于0的点对应y=-1的点，如下图所示：

    注：有的资料上定义特征到结果的输出函数，与这里定义的

实质是一样的。为什么？因为无论是，还是

，不影响最终优化结果。下文你将看到，当我们转化到优化

的时候，为了求解方便，会把yf(x)令为1，即yf(x)是

y(w^x + b)，还是y(w^x - b)，对我们要优化的式子max1/||w||已无影响。

    （有一朋友飞狗来自Mare_Desiderii，看了上面的定义之后，问道：请教一下

SVM functional margin 为=y(wTx+b)=yf(x)中的Y是只取1和-1 吗？y的唯一作

用就是确保functional margin的非负性？真是这样的么？当然不是，详情请见本

文评论下第43楼）

    当然，有些时候，或者说大部分时候数据并不是线性可分的，这个时候满足

这样条件的超平面就根本不存在(不过关于如何处理这样的问题我们后面会讲)，

这里先从最简单的情形开始推导，就假设数据都是线性可分的，亦即这样的超平

面是存在的。

    换言之，在进行分类的时候，遇到一个新的数据点x，将x代入f(x) 中，如果f(x)小于0则将x的类别赋为-1，如果f(x)大于0则将x的类别赋为1。

    接下来的问题是，如何确定这个超平面呢？从直观上而言，这个超平面应该是最适合分开两类数据的直线。而判定“最适合”的标准就是这条直线离直线两边的数据的间隔最大。所以，得寻找有着最大间隔的超平面。

1.3、函数间隔Functional margin与几何间隔Geometrical margin

    在超平面w*x+b=0确定的情况下，|w*x+b|能够表示点x到距离超平面的远近，而通过观察w*x+b的符号与类标记y的符号是否一致可判断分类是否正确，所以，可以用(y*(w*x+b))的正负性来判定或表示分类的正确性。于此，我们便引出了函数间隔（functional margin）的概念。

   定义函数间隔（用表示）为：

                                                

    而超平面(w，b)关于T中所有样本点(xi，yi)的函数间隔最小值（其中，x是特征，y是结果标签，i表示第i个样本），便为超平面(w, b)关于训练数据集T的函数间隔：

            = mini  (i=1，...n)

    但这样定义的函数间隔有问题，即如果成比例的改变w和b（如将它们改成2w和2b），则函数间隔的值f(x)却变成了原来的2倍（虽然此时超平面没有改变），所以只有函数间隔还远远不够。

    事实上，我们可以对法向量w加些约束条件，从而引出真正定义点到超平面的距离--几何间隔（geometrical margin）的概念。

    假定对于一个点 x ，令其垂直投影到超平面上的对应点为 x0 ，w 是垂直于超平面的一个向量，为样本x到分类间隔的距离，如下图所示：

    有，其中||w||表示的是范数。

    又由于 x0 是超平面上的点，满足 f(x0)=0 ，代入超平面的方程即可

算出：

                                                        
γ

    （有的书上会写成把||w|| 分开相除的形式，如本文参考文献及推荐阅读条目11，其中，||w||为w的二阶泛数）

    为了得到的绝对值，令乘上对应的类别 y，即可得出几何间隔（用表示）的定义：

                                                        

    从上述函数间隔和几何间隔的定义可以看出：几何间隔就是函数间隔除以||w||，而且函数间隔y*(wx+b) = y*f(x)实际上就是|f(x)|，只是人为定义的一个间隔度量，而几何间隔|f(x)|/||w||才是直观上的点到超平面的距离。

1.4、最大间隔分类器Maximum Margin Classifier的定义

    对一个数据点进行分类，当超平面离数据点的“间隔”越大，分类的确信度（confidence）也越大。所以，为了使得分类的确信度尽量高，需要让所选择的超平面能够最大化这个“间隔”值。这个间隔如下图中的gap / 2所示。

    通过由前面的分析可知：函数间隔不适合用来最大化间隔值，因为在超平面固定以后，可以等比例地缩放w的长度和b的值，这样可以使得的值任意大，亦即函数间隔可以在超平面保持不变的情况下被取得任意大。但几何间隔因为除上了，使得在缩放w和b的时候几何间隔的值是不会改变的，它只随着超平面的变动而变动，因此，这是更加合适的一个间隔。所以，这里要找的最大间隔分类超平面中的“间隔”指的是几何间隔。

   于是最大间隔分类器（maximum margin classifier）的目标函数可以定义为：

    同时需满足一些条件，根据间隔的定义，有

    其中，s.t.，即subject to的意思，它导出的是约束条件。

    回顾下几何间隔的定义可知：如果令函数间隔等于1（之所以令等于1，是为了方便推导和优化，且这样做对目标函数的优化没有影响，至于为什么，请见本文评论下第42楼回复），则有 = 1 / ||w||且，从而上述目标函数转化成了

    这个目标函数便是在相应的约束条件下，最大化这个1/||w||值，而1/||w||便是几何间隔。   

    如下图所示，中间的实线便是寻找到的最优超平面（Optimal Hyper Plane），其到两条虚线的距离相等，这个距离便是几何间隔，两条虚线之间的距离等于2，而虚线上的点则是支持向量。由于这些支持向量刚好在边界上，所以它们满足（还记得我们把 functional margin 定为 1 了吗？上节中：处于方便推导和优化的目的，我们可以令=1），而对于所有不是支持向量的点，则显然有。

    OK，到此为止，算是了解到了SVM的第一层，对于那些只关心怎么用SVM的朋友便已足够，不必再更进一层深究其更深的原理。