模拟退火算法(SA)简单介绍,附用python3求解最大值案例
简介
模拟退火算法(Simulate Anneal,SA)是一种通用概率演算法,用来在一个大的搜寻空间内找寻命题的最优解。其思想借鉴于固体的退火原理,当固体的温度很高的时候,内能比较大,固体的内部粒子处于快速无序运动,当温度慢慢降低的过程中,固体的内能减小,粒子的慢慢趋于有序,最终,当固体处于常温时,内能达到最小,此时,粒子最为稳定。模拟退火算法便是基于这样的原理设计而成。
套用知乎上的形象描述:
一个锅底凹凸不平有很多坑的大锅,晃动这个锅使得一个小球使其达到全局最低点。一开始晃得比较厉害,小球的变化也就比较大,在趋于全局最低的时候慢慢减小晃锅的幅度,直到最后不晃锅,小球达到全局最低。
爬山算法
介绍模拟退火,一般会提到爬山算法。爬山算法是一种简单的贪心搜索算法,该算法每次从当前解的临近解空间中选择一个最优解作为当前解,直到达到一个局部最优解。
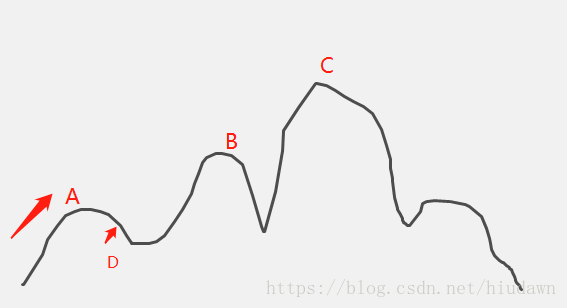
如上图所示,如果是简单的爬山算法,那么从出发点开始,遇到A就不会再爬了(肯定不会往D移动),因为A是其附近的一个比较高的点,再往两边走都会下降。这就是陷入了局部最优解。爬山算法可以说是完全“贪心”的,鼠目寸光,丝毫不知道后面还有C等着它。
模拟退火思想
事实上,与爬山算法相似,模拟退火也是一种贪心算法,但它到达A之后,有一定概率往D移动,并且随着时间推移(温度逐渐下降),这个概率会逐渐降低(这样最终才能稳定)。这个过程很像金属退火的那个过程,故退火算法因此得名。那么这个一定概率怎么表达呢,根据热力学原理,在温度为T时,出现能量差降温的概率为:
上面的公式是金属冶金的,这个公式翻译成模拟退火算法就是:假设现在位于某个位置 x0 x 0 ,现在随机发生了一个位移到达 x0+Δx x 0 + Δ x ,当发生位移后因变量 y|x=x0+Δx y | x = x 0 + Δ x 小于原来的 y|x=x0 y | x = x 0 ,那么我接受这个位移的概率为:
其中这里的T是模拟退火中设置的一个参数。当然,如果 y|x=x0+Δx>y|x=x0 y | x = x 0 + Δ x > y | x = x 0 ,那么那个位移肯定会被接受,这个 p(Δx)=1 p ( Δ x ) = 1 。
有趣的比喻
爬山算法:兔子朝着比现在高的地方跳去。它找到了不远处的最高山峰。但是这座山不一定是珠穆朗玛峰。这就是爬山算法,它不能保证局部最优值就是全局最优值。(非常懒,一开始看到比现在高的就接受)
模拟退火:兔子喝醉了。它随机地跳了很长时间。这期间,它可能走向高处,也可能踏入平地。但是,它渐渐清醒了并朝最高方向跳去。这就是模拟退火。(一开始很激动,到处试探,变化大。后面心累了,逐渐减缓了步伐,朝向此时此刻的最高点爬去)
算法实现
这里用SA来求解 y=10×sin(5x)+7×cos(4x) y = 10 × s i n ( 5 x ) + 7 × c o s ( 4 x ) 在的 x=0和10 x = 0 和 10 之间的最大值
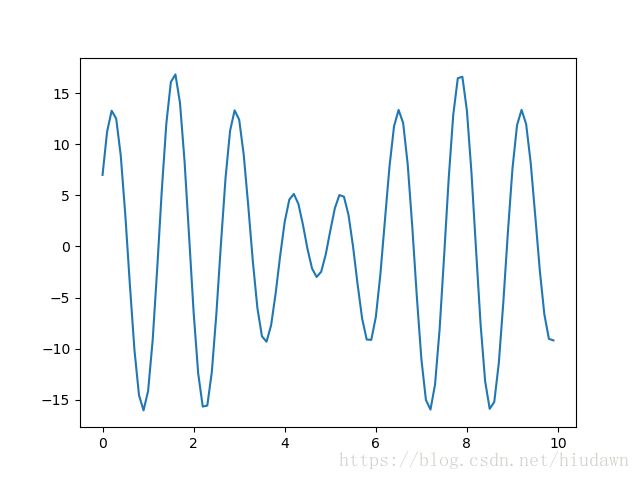
算法步骤:
1.初始化温度 T T 、降温系数 α α 、最小温度 Tmim T m i m 以及一个随机的可行解 (x,y) ( x , y )
2.当 T>Tmim T > T m i m ,进行下面步骤,否则返回结果
3.随机发生扰动 Δx Δ x
4.计算发生扰动后的 Δy值 Δ y 值 ,大于0就接受这个扰动,小于0就以 p(Δx)=e−ΔxT p ( Δ x ) = e − Δ x T 概率接受。
5.更新最佳 (x,y) ( x , y )
5.循环步骤3到4 n次(自己设定的参数)。
6. T=αT T = α T
7.返回步骤2
代码
import matplotlib.pyplot as plt
import math
import random
"""
函数里面所有以plot开头的函数都可以注释掉,没有影响
求解的目标表达式为:
y = 10 * math.sin(5 * x) + 7 * math.cos(4 * x) x belongs to (0,10)
"""
def main():
plot_obj_func()
T_init = 100 # 初始最大温度
alpha = 0.90 # 降温系数
T_min = 1e-3 # 最小温度,即退出循环条件
T = T_init
x = random.random() * 10 # 初始化x,在0和10之间
y = 10 * math.sin(5 * x) + 7 * math.cos(4 * x)
results = [] # 存x,y
while T > T_min:
x_best = x
# y_best = float('-inf') # 设置成这个有可能会陷入局部最优,不一定全局最优
y_best = y # 设置成这个收敛太快了,令人智熄
flag = 0 # 用来标识该温度下是否有新值被接受
# 每个温度迭代50次,找最优解
for i in range(50):
delta_x = random.random() - 0.5 # 自变量进行波动
# 自变量变化后仍要求在[0,10]之间
if 0 < (x + delta_x) < 10:
x_new = x + delta_x
else:
x_new = x - delta_x
y_new = 10 * math.sin(5 * x_new) + 7 * math.cos(4 * x_new)
# 要接受这个y_new为当前温度下的理想值,要满足
# 1y_new>y_old
# 2math.exp(-(y_old-y_new)/T)>random.random()
# 以上为找最大值,要找最小值就把>号变成<
if (y_new > y or math.exp(-(y - y_new) / T) > random.random()):
flag = 1 # 有新值被接受
x = x_new
y = y_new
if y > y_best:
x_best = x
y_best = y
if flag:
x = x_best
y = y_best
results.append((x, y))
T *= alpha
print('最优解 x:%f,y:%f' % results[-1])
plot_final_result(results)
plot_iter_curve(results)
# 看看我们要处理的目标函数
def plot_obj_func():
"""y = 10 * math.sin(5 * x) + 7 * math.cos(4 * x)"""
X1 = [i / float(10) for i in range(0, 100, 1)]
Y1 = [10 * math.sin(5 * x) + 7 * math.cos(4 * x) for x in X1]
plt.plot(X1, Y1)
plt.show()
# 看看最终的迭代变化曲线
def plot_iter_curve(results):
X = [i for i in range(len(results))]
Y = [results[i][1] for i in range(len(results))]
plt.plot(X, Y)
plt.show()
def plot_final_result(results):
X1 = [i / float(10) for i in range(0, 100, 1)]
Y1 = [10 * math.sin(5 * x) + 7 * math.cos(4 * x) for x in X1]
plt.plot(X1, Y1)
plt.scatter(results[-1][0], results[-1][1], c='r', s=10)
plt.show()
if __name__ == '__main__':
# for i in range(100):
main()
运行结果
初始温度 T=100 T = 100
降温系数 α=0.90 α = 0.90
每个T里面再循环 50 50 次取当前温度最佳
得到全局最优的概率大概有 100% 100 %
运行得到的最优解:
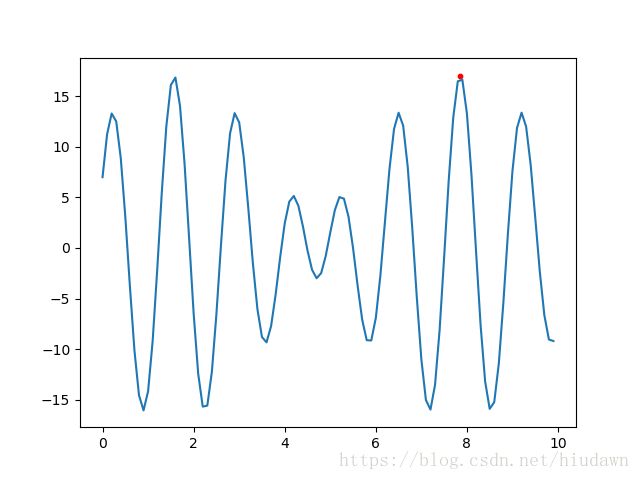
收敛之快令人发指:
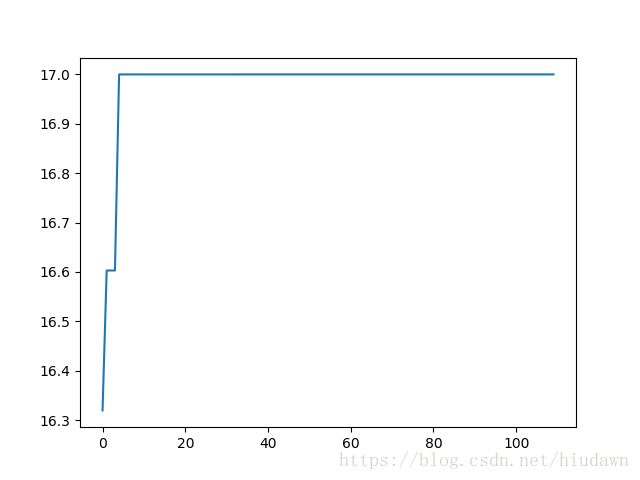
后话
这里不知道改了什么,同样一个目标函数,用遗传算法和模拟退火效率截然不同。大概是弄错了吧2333,毕竟水平有限。这么一对比,似乎退火在解决这种弱智问题上还好用点。不过其实仔细想下,两个算法各自的优缺点还是比较明显的。
遗传算法:优点是能很好的处理约束,能很好的跳出局部最优,最终得到全局最优解,全局搜索能力强;缺点是收敛较慢,局部搜索能力较弱,运行时间长,且容易受参数的影响。(一次放了一堆兔子,品种不好的就把人家丢掉)
模拟退火:优点是局部搜索能力强,运行时间较短;缺点是全局搜索能力差,容易受参数的影响。(一次只放一只喝醉酒的兔子,酒醒之时即是远方)