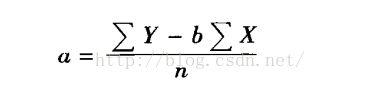用Python学习统计学基础-6

十四、使用相关系数检验关系

    检验变量之间的关系而不是群体之间的差异； 只检验两个变量之间的关系；所要应用的合适的检验统计是相关系数的t检验。实例：婚姻质量和父母-子女关系水平--之间关系的检验。零假设，没有关系；研究假设，存在关系。显著水平设置为.05。

import scipy.stats as stats
#婚姻质量
x=[76,81,78,76,76,78,76,78,98,88,76,66,44,67,65,59,87,77,79,85,68,76,77,98,99,98,87,67,78]  
#父母-子女关系 水平
y=[43,33,23,34,31,51,56,43,44,45,32,33,28,39,31,38,21,27,43,46,41,41,48,56,55,45,68,54,33]  
r, p=stats.pearsonr(x,y)
print r
print p

输出

0.393418620974
0.0347359313295

计算得到 r=0.393 p=0.034，说明两个变量之间的关系是由于随机因素引起的可能性小于5%，因此认为两个变量之间的关系是显著的。

十五、使用线性回归

估计是以过去的结果估计未来结果的活动，比如用高中的平均成绩估计大学的平均成绩。要进行这样的估计就必须建立回归等式(regression equation)，并建立回归线(regression line)。立回归线也称作最优拟合线(line of best fit)。用x表示高中平均成绩，用y表示大学成绩，这就是变量y对变量x的回归，即y依据x被估计。每一个具体的数据点和回归线的距离就是估计误差(error in prediction)。给定了回归线，就可以用回归线来估计任何值。回归线的一般公式：

Python代码，分为三部分，1)调用stats.lintegress(x,y)得到斜率和截距，2）定义回归函数， 3）用np.linspace生成xdata， 然后用plt绘图。

import numpy as np
import matplotlib.pylab as plt
from scipy import stats
x = [3.5, 2.5, 4.0, 3.8, 2.8, 1.9, 3.2, 3.7, 2.7, 3.3]   #高中平均成绩
y = [3.3, 2.2, 3.5, 2.7, 3.5, 2.0, 3.1, 3.4, 1.9, 3.7]   #大学平均成绩
slope, intercept, r_value, p_value, std_err = stats.linregress(x,y)
slope = round(slope,3)
intercept = round(intercept,3)
print slope, intercept

def f(x, a, b):
    return a + b*x

xdata = np.linspace(1, 5, 20)
plt.grid(True)
plt.xlabel('x axis')  
plt.ylabel('y axis') 
plt.text(2.5, 4.0, r'$y = ' + str(intercept) + ' + ' + str(slope) +'*x$', fontsize=18)
plt.plot(xdata, f(xdata, intercept,slope), 'b', linewidth=1)
plt.plot(x,y,'ro')
plt.show()

输出

0.704 0.72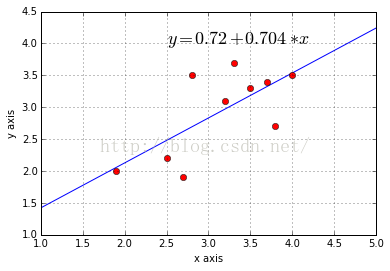

十六、卡方和其他非参数检验

参数检验假定所使用的数据集有确定的特征（总体分布已知），并且样本大可以代表总体，如果不满足上述假定 ，则需要使用非参数检验(Nonparametric tests)方法。卡方检验（chi square test）是常用的非参数检验之一。可以用于确定在频数分布中观察到的结果是否就是你随机预期的结果。如问卷调查中对教育券的支持情况，分为赞同、中立、反对三种选择。

卡方值的计算

然后查表得到p值。用scipy.stats.chisquare(f_obs, f_exp=None, ddof=0, axis=0)可以很方便地计算。

python代码

from scipy.stats import chisquare
f_obs = [23, 17, 50]       #赞同、中立、反对
f_exp = [30, 30, 30]
chisq, p = chisquare(f_obs, f_exp)
print chisq
print p

输出

20.6
3.36330951857e-05

计算结果p值小于.000，这说明，这三个分类的频数相等时非常不可能的。

后记

《爱上统计学》书上基本的内容就学完了，书上介绍的多元方差分析、重复测量的方差分析等其他高级内容等遇到再学习吧。