基于决策树和朴素贝叶斯算法对Adult数据集分类

基于决策树和朴素贝叶斯算法对Adult数据集分类

1、数据集介绍

机器学习算法需要作用于数据，数据的属性和特征决定了机器学习算法是否适用，同时，数据质量的好坏也直接决定算法表现的好坏。这篇博客选择在Adult数据集上进行实验。

Adult数据集

该数据从美国1994年人口普查数据库中抽取而来，因此也称作“人口普查收入”数据集，共包含48842条记录，年收入大于50k$的占比23.93%，年收入小于50k$的占比76.07%，数据集已经划分为训练数据32561条和测试数据16281条。该数据集类变量为年收入是否超过50k$，属性变量包括年龄、工种、学历、职业等14类重要信息，其中有8类属于类别离散型变量，另外6类属于数值连续型变量。该数据集是一个分类数据集，用来预测年收入是否超过50k$。

数据集特征：	多变量	记录数：	48842	领域：	社会
属性特征：	类别型、整数型	属性数目：	14	捐赠日期：	1996-05-01
相关应用：	分类	缺失值？	有	网站点击数：	1059012

14个属性变量具体介绍如下：

属性名	类型	含义
age	continuous	年龄
workclass	discrete	工作类别
fnlwgt	continuous	序号
education	discrete	受教育程度
education-num	continuous	受教育时间
marital-status	discrete	婚姻状况
occupation	discrete	职业
relationship	discrete	社会角色
race	discrete	种族
sex	discrete	性别
capital-gain	continuous	资本收益
capital-loss	continuous	资本支出
hours-per-week	continuous	每周工作时间
native-country	discrete	国籍

训练集中属性age的最小值为17，最大值为90，平均年龄为38.6，具体分布直方图如下：

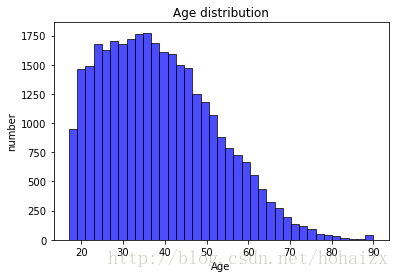
训练集中属性education-num最小值为1，最大值为16，平均值为10，将其划分为“<5”、“5-10”和“>10”三个区间，分布饼图如下：

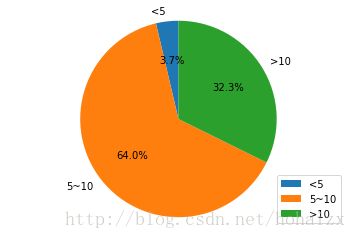
训练集中属性hours-per-week取值虽然分布在1到99之间，但基本集中在40附近，具体分布直方图如下：

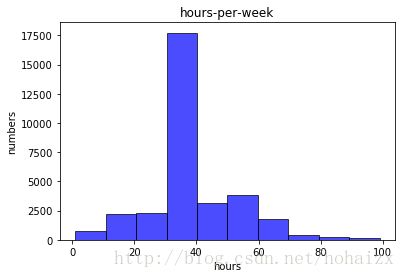
8个离散型属性变量中，workclass有“Private”等8个取值；education有“Bachelors”等16个取值；marital-status有“Married-civ-spouse”等7个取值；occupation有“Tech-support”等14个取值；relationship有“Wife”等6个取值；race有“White”等5个取值；sex取“Female”和“Male”；native-country有“United-States”等41个取值。
因为adult数据集是一个分类数据集，并且属性变量的取值既有连续型又有离散型，因此本实验决定采用决策树和贝叶斯算法。决策树算法计算比较简单，解释性强，比较适合处理有缺失属性值的数据样本。贝叶斯算法源于古典数学理论，有着坚实的数学基础，分类效率稳定，同样算法比较简单，对缺失数据不太敏感。

2、实验方案

2.1、决策树算法

决策树算法和人类在进行决策时的处理机制类似，依据对一系列属性取值的判定得出最终决策。决策树是一棵树结构，其每个非叶子节点表示一个特征属性上的测试，每个分支表示这个特征属性在某个值域上的输出，而每个叶子节点对应于最终决策结果。使用决策树进行决策的过程就是从根节点开始，测试待分类项中相应的特征属性，并按照其值选择输出分支，直到到达叶子节点，将叶子节点对应的类别作为决策结果。
决策树学习的目的是产生一棵泛化性能强，即处理未见示例能力强的决策树。其基本流程遵循“分而治之”的策略，算法伪代码如下图所示：

输入：训练集D={(x_1,y_1),(x_2,y_2),⋯,(x_m,y_m)};
     属性集A={a_1,a_2,⋯,a_d}.
过程：函数TreeGenerate(D,A)
1: 生成节点node
2: if  D中样本全属于同一类别C then
3:    将node标记为C类叶节点；return
4: end if
5: if  A=∅ or D中样本在A上取值相同 then
6:    将node标记为叶节点，其类别标记为D中样本数最多的类；return
7: end if
8: 从A中选择最优 划分属性a_*;
9: for a_*的每一个取值a_*^v do
10:    为node生成一个分支；令D_v表示D中在a_*上取值为a_*^v的样本子集；
11:    if D_v=∅ then
12:       将分支节点标记为叶节点，其类别标记为D中样本最多的类；return
13:    else
14:       以TreeGenerate(D_v,A\{a_*})为分支节点
15:    end if
16: end for
输出：以node为根节点的一棵决策树

上述算法最关键的是第8行，即如何选择最优划分，选择的标准是什么。一般而言，随着划分的不断进行，决策树每个分支包含的样本会越来越属于同一类，即节点的“纯度”越来越高。但是为了得到一棵泛化性能强的决策树，根据“奥卡姆剃刀”原则：越是小型的决策树越优于大型的决策树，我们希望最终得到的决策树规模越小越好。因此我们选择划分后能够将样本“纯度提升”最大的那个属性作为最优划分。
为了度量样本“纯度提升”，我们需要引入一些概念。

2.1.1、信息熵

信息熵是信息论之父香浓从热力学概念“熵”中借鉴过来的，在热力学中熵表示分子的混乱程度，香浓用信息熵来描述信息的不确定度。信息熵的计算公式定义如下：

Ent(D)=−∑k=1|y|pklog2pk(1) (1) E n t ( D ) = − ∑ k = 1 | y | p k l o g 2 p k

其中， pk p k 代表样本集合D中第k类样本所占的比例，|y|为样本集合D的类别数目。Ent(D)越小，则信息的不确定性越小，信息的纯度越高。

2.1.2、信息增益

当我们选择一个属性进行划分后，信息的纯度将增加，信息的不确定性将随之减少。我们用信息增益来度量样本纯度的提升。假设离散属性a有V个可能的取值 {a1,a2,⋯,aV} { a 1 , a 2 , ⋯ , a V } ，若使用a来对样本集D进行划分，则会产生V个分支节点，其中第v个分支节点包含了D中所有在属性a上取值为 av a v 的样本，记为 Dv D v 。因此我们可以将信息增益的公式记为如下：

Gain(D,a)=Ent(D)−∑v=1V|Dv||D|Ent(Dv)(2) (2) G a i n ( D , a ) = E n t ( D ) − ∑ v = 1 V | D v | | D | E n t ( D v )

因此，信息增益越大，则意味着使用属性a进行划分获得的“纯度提升”越大。著名的ID3决策树算法就是以信息增益为准则来选择划分属性。

2.1.3、连续值处理

由于连续属性的可取值数目不再有限，因此，不能直接根据连续属性的可取值来对节点进行划分。此时，需要对连续属性离散化，最简单的策略是采用二分法将连续属性值一分为二。在本实验中，通过对连续数据的取值观察，最终确定将age、education-num、captional-gain、captional-loss和hours-per-week划分为10、8、12、12、12个区间。

2.2、朴素贝叶斯算法

贝叶斯分类是一类分类算法的总称，这类算法以贝叶斯定理为基础，故统称贝叶斯分类。贝叶斯分类与常用的决策树、支持向量机（SVM）等判别型分类器不同，贝叶斯分类属于生成型模型，生成型模型最大的特点是先对联合概率分布 p(x,c) p ( x , c ) 建模，然后再由此获得 p(c|x) p ( c | x ) 。根据条件概率公式有：

p(c|x)=p(x,c)p(x)(3) (3) p ( c | x ) = p ( x , c ) p ( x )

基于贝叶斯定理，p(c|x)可写为：

p(c|x)=p(c)p(x|c)p(x)(4) (4) p ( c | x ) = p ( c ) p ( x | c ) p ( x )

其中， p(c) p ( c ) 是类先验概率； p(x|c) p ( x | c ) 是样本x相对于类标记c的类条件概率； p(x) p ( x ) 是用于归一化的“证据”因子。对于给定的x，“证据”因子 p(x) p ( x ) 与类标记无关，因此估计 p(c│x) p ( c │ x ) 的问题转化为如何基于训练数集D来估计类先验概率p(c)和类条件概率 p(x|c) p ( x | c ) 。
类先验概率 p(c) p ( c ) 表达了样本空间中各类样本所占的比例，根据大数定律，当训练集包含充足的独立同分布样本时， p(c) p ( c ) 可以通过各类样本出现的频率进行估计。但是对类条件概率 p(x|c) p ( x | c ) 来说，由于它涉及关于x的所有属性的联合概率，直接根据样本出现的频率来估计将会遇到严重困难。即使是每个属性取值均为二值，d个属性构成的样本空间也将达到 2d 2 d ，这个数字远远超过了训练数据样本数m。一方面，依靠计算机扫面统计将变得几乎不太可能；另一方面，由于数据稀疏性，很多样本取值在训练集中根本没有出现，直接使用频率估计概率显然不可行。常用的策略是先假定类条件概率服从某种形式的概率分布，再基于训练样本对概率分布的参数进行估计。
朴素贝叶斯分类是贝叶斯分类中最简单，也是最常见的一种分类方法，广泛用于新闻分类、病人分类等任务中。朴素贝叶斯分类器的“朴素”体现在：假设所有属性相互独立。基于属性条件独立性假设，上式（4）可重写为：

p(c|x)=p(c)p(x|c)p(x)=p(c)p(x)∏i=1dp(xi|c)(5) (5) p ( c | x ) = p ( c ) p ( x | c ) p ( x ) = p ( c ) p ( x ) ∏ i = 1 d p ( x i | c )

其中d为属性数目，x_i为x在第i个属性上的取值。
朴素贝叶斯分类的流程如下图所示：

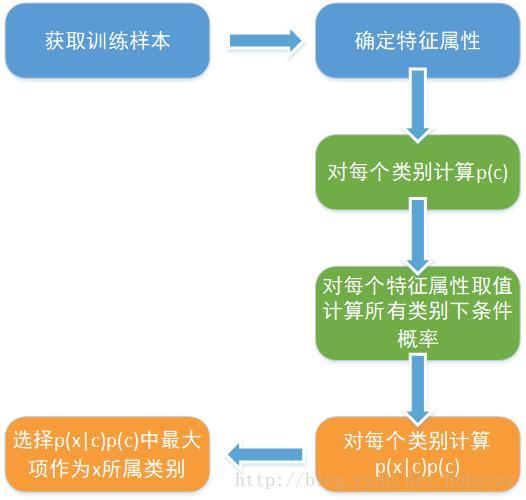
2.2.1、连续值处理

同样对于取值为无限的连续型属性变量，在利用朴素贝叶斯算法进行分类时，也需要进行连续值平滑处理。在本实验中，将age、captional-gain、captional-loss和hours-per-week划分为10、3、3、20个区间。因为education-num和education表达的是相同的意思，所以将其去除。另外，在本实验中，也对部分离散型属性进行了重新归类，将相似的取值归为一类，既减少了属性取值数，也提高了模型泛化能力。

2.2.2、平滑处理

因为训练样本的数量有限，在训练数据集中，可能出现某个属性的某个取值为零的情况，那么这个条件概率值为0，导致整个后验概率值为0，为了避免其他属性携带的信息被训练集中未出现的属性值“抹去”，在进行概率估计时通常要加上平滑项，常用拉普拉斯平滑，这时条件概率公式可以修正为：

p^(xi|c)=|Dc,xi|+1|Dc|+Ni(6) (6) p ^ ( x i | c ) = | D c , x i | + 1 | D c | + N i

其中 Ni N i 第i个属性可能的取值数。

3、实验结果及对比

本次实验中，采用决策树算法的准确率为80.37%，采用朴素贝叶斯算法的准确率为81.93%。

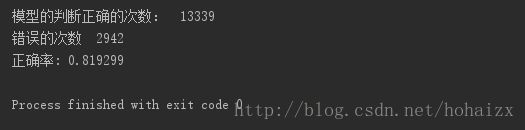
决策树算法准确率较低的原因可能是没有进行剪枝操作，可能导致学习到的模型出现过拟合情况。同时，在采用朴素贝叶斯算法时，对数据进行了更加细致的预处理，减少了冗余的特征，归并了类似的特征取值等，这些都会提升朴素贝叶斯模型的准确率。
决策树算法和朴素贝叶斯算法是两类非常常用的分类算法，两者都非常容易理解，分类过程非常直观，且可解释性良好，模型训练也比较简单。因此广泛应用于医学、制造业、商业等诸多领域。

参考文献

周志华 机器学习
算法杂货铺——分类算法之朴素贝叶斯分类(Naive Bayesian classification)