3D地形编程——之GeoMipMap基础(4)
m_pPatches[iPatch].m_iLOD= 0;
else if( m_pPatches[iPatch].m_fDistance<1000 )
m_pPatches[iPatch].m_iLOD= 1;
else if( m_pPatches[iPatch].m_fDistance<2500 )
m_pPatches[iPatch].m_iLOD= 2;
else if( m_pPatches[iPatch].m_fDistance>=2500 )
m_pPatches[iPatch].m_iLOD= 3;
这些距离使得速度和细节有效的结合起来。如果演示在你的图像卡上显示有点缓慢,你也许想改变这些距离,但是别这样做。我们将在这章后面做一些速度的最优化,所以别绝望!这些就是所有Geomipmapping图块更新内容……对现在来说,至少是这样。现在是时候到了任何地形实现有趣的部分:渲染它!
Geomipmapping的渲染
这也许是你将在这章碰到的最难的一节,这并不是很坏。它一时有点难懂,但是我会带你走过它。
一点一点的把东西划分开
最简单的渲染每个东西的方法是,我们需要的渲染就是把单独的渲染程序一点点的划分开,所以代码不会变得很臃肿。这可能会增加一些函数头,但是只要我们把那些东西弄的整齐漂亮,就不会太糟糕。
我计算它的方法,Geomipmapping类应该有一个高层次渲染函数,能把低层的函数连续添加进去。例如,最高层的渲染函数是Render。跟着Render的是RenderPatch、RenderFan。RendeVertex做为最低层。使用这些函数,函数头数量会增长一点,但值得注意的是我们减少了代码丑陋的地方。这个交易是值得的。如果你花了时间很难理解我计划用的这个设计,看图5.14。随着实现我们的渲染系统,让我们从低起点向高的路线工作。
RenderVertex函数
系统的顶点渲染函数不是什么特别的东西,但坦诚的说,它很小。我们会经常调用它,让它成为一个理想的内联(inline)函数。RenderVertex基于阴影值设置顶点的颜色,阴影值是从光照图取出和光线颜色的RGB各分量值复合而来。这时RenderVertex传送纹理坐标给渲染API(为细节映射,如果需要也为纹理颜色)。在那之后,简单的你需要传送的顶点坐标缩放比例给渲染API。这就完成了!
图5.14 Geomipmapping类的渲染构造。
RenderFan函数
每个Geomipmapping的块都能分散成许多小扇形,不管是1个块还是256个块都是如此。使用这个函数就清理了在RenderPatch里的很多代码,下一节会讨论RenderPatch。
所有块渲染函数做的就是渲染单个三角形扇面。因此,函数需要接收的参数有扇形的中心点和扇形一边的长度,这样函数就能渲染它。RenderFan也需要获取块的邻接信息。好吧,是一些信息。邻接信息是单独的扇形的。如果因为一个比较粗糙的块在它右边需要删除一个顶点,但是当前扇形是在块的中间,这时邻接结构会显示所有邻接是true。(只有在块的右面这条边的扇形需要担心顶点的移除。)如果这个扇形正在被渲染,然而,顶点的移除是需要的。例如,如果这个扇形在块的右面的边上,并且在当前块的右边的块是更粗糙的细节级别(LOD),这时当前扇形就需要移除渲染右顶点。
RenderPatch函数
块渲染函数是整个渲染系统中最为至关紧要的,因为如果不渲染块你就不会看到地形。大部分的反裂缝步骤就被放在这个函数里,其余反裂缝部分(顶点的移除)被放在RenderFan函数中。记住我给你看的伪代码在前面的“尔裂缝的艺术在哪里?”好了,我们需要实现它。我们需要填充一个“邻接结构,”它是个简单的数据结构包含了4个布尔值(boolean)来标识周围的块(左、右、上和下的块)是否比当前块细节级别高。如果邻接值被标记ture,我们就能标准的渲染这边的块,因为我们不需要特殊计量来防止裂缝。如果它被标记为false,我们需要做特别的测算。
【注释
当我们在这章谈到“较高级别细节”,意思是“更低的地形细节。”这是因为我们的级别系统是从高(低数量的地形细节)开始的,并且级别越低地形细节越多,由级别0结束是最多地形细节。只要别在我们谈论高/低细节级别时搞混就行了。】(意思是细节级别有0~3,从0开始到3地形的细致程度越来越少。)
在反裂缝步骤后,我们需要计算出从哪里开始渲染三角形扇面。这个比听起来稍微复杂点,但不是很难。这里面最难的部分是试图计算出三角形扇面的中心点距离。在这完成后,我们会感觉好到极点!
我们怎样计算出每个扇面的中心点相互的距离?好吧,我着手的方法,虽然它看起来有点奇怪,首先以单个块的大小开始尝试计算块被划分成了多少,由此得到每个扇相互中心点长度。首先从除数、块的大小开始,用while循环计算块的总大小被划分成多少。例如,如果块是0级,我们用单个块大小划分它本身的大小,这样我们渲染的每个扇都产生1个单位的长度。(我们不想缩放顶点直到我们运行RenderVertex函数。)一个级别1的块,每个扇的距离就会是2个单位,2级就有8个单位,等等。前面计算的代码如下:
fDivisor= ( float )m_iPatchSize;
fSize = ( float )m_iPatchSize;
iLOD = m_pPatches[iPatch].m_iLOD;
//find out how many fan divisions we are going to have
While( iLOD-->=0)
iDivisor= fDivisor/2.0f;
//the size between the center of each triangle fan
fSize/= fDivisor;
(意思是以级别0为基准的话,计算出大边上有多少个小边,因为是2的倍数,所以用循环计算被划分了多少,用总长度除这个分块数就是扇形距离的长度了,间隔的基准单位是以0级别的。原文循环中那条语句可能有点问题。)
这个计算还不是完全正确的;当我们用时,所产生的地形看起来象图5.15。
图5.15 哎呀!它看上去象是一些错误计算产生的!
这个计算哪里出错了呢?好,有个简单东西被我们做错了。我们想这个除数变量,fDivisor,是2的幂。记住当除数等于块的大小时,扇的距离是0级的1个单位长度对吧?好,从一个中心点到另一个中心点,我们需要至少2个单位间隔(看图5.16)。
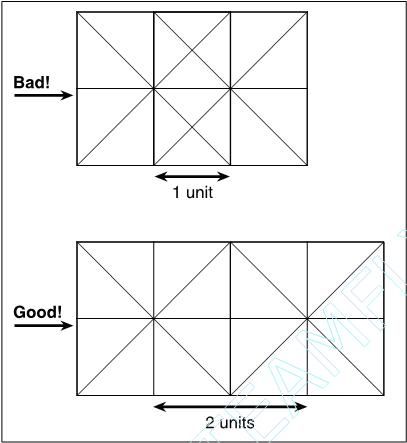
你看到图5.16中顶部的一对扇形相互怎样重叠(产生出一个相当糟糕的结果)的了么?它们是1个单位的间隔。看到在底部的2个扇形完美的恰当的在一起了么?它们是2个单位间隔。好了,我们需要改变先前扇的中心点计算,这样使块的最小间隔是2个单位。你问我们怎么做?这很简单。我们只要设置除数变量的初始值是块大小的减1,这使除数变量一直是2的幂,由此修正我们之前的所有问题。看新代码。(fDivisor变成iDivisor这样我们能提升一点计算速度。)
图5.16 1个扇中心间隔为1个单位与1个块是2个单位间隔。
fSize = ( float )m_iPatchSize;
iDivisor= m_iPatchSize-1;
iLOD = m_pPatches[iPatch].m_iLOD;
//find out how many fan divisions we are going to have
While( iLOD-->=0 )
iDivisor= iDivisor>>1;
//the size between the center of each triangle fan
fSize/= iDivisor;
在这完成之后,渲染块的三角形扇变得轻松。只需要确定渲染的起点是fSize的一半因为第一个扇的中心点在那里。我们需要检查是否每个扇都需要移除顶点。意味着我们需要用到