Java How to Program习题_第七章_数组及动态数组(Array and ArrayList)——第一部分(7.1 - 7.22)
这一章的习题非常多,而且都有一定的难度(如海龟绘图、骑士游历等)。
我希望能够全部做完,但是时间有限,最好还是加快进度往后面的章节进步吧。所以,先把已经完成的习题放上来吧。
| Self-Review Exercises 7.1 Fill in the blank(s) in each of the following statements: a) Lists and tables of values can be stored in arrays and collections. b) An array is a group of variables (called elements or components) containing values that all have the same type. c) The enhanced for statement allows you to iterate through an array’s elements without using a counter. d) The number used to refer to a particular array element is called the element’s index (or subscript or position number). e) An array that uses two indices is referred to as a(n) two-dimensional array. f) Use the enhanced for statement for (double d: Numbers) to walk through double array numbers. g) Command-line arguments are stored in array of Strings called args by convention. h) Use the expression args.length to receive the total number of arguments in a command line. Assume that command-line arguments are stored in String[] args. i) Given the command java MyClass test, the first command-line argument is test. j) A(n) ellipsis (…) in the parameter list of a method indicates that the method can receive a variable number of arguments. 7.2 Determine whether each of the following is true or false. If false, explain why. a) An array can store many different types of values. (F) b) An array index should normally be of type float. (F) c) An individual array element that’s passed to a method and modified in that method will contain the modified value when the called method completes execution. (F) d) Command-line arguments are separated by commas. (F) 7.3 Perform the following tasks for an array called fractions: a) Declare a constant ARRAY_SIZE that’s initialized to 10. (final int ARRAY_SIZE = 10; ) b) Declare an array with ARRAY_SIZE elements of type double, and initialize the elements to 0. (double[] fractions = new array[ARRAY_SIZE]; ) c) Refer to array element 4. (fractions[4]) d) Assign the value 1.667 to array element 9. (fractions[9] = 1.667) e) Assign the value 3.333 to array element 6. (fractions[6] = 3.333) f) Sum all the elements of the array, using a for statement. Declare the integer variable x as a control variable for the loop. ( double sum = 0.0; for (int x = 0; x < fractions.length; x++) total += fractions[x]; ) 7.4 Perform the following tasks for an array called table: a) Declare and create the array as an integer array that has three rows and three columns. Assume that the constant ARRAY_SIZE has been declared to be 3. ( final int ARRAY_SIZE = 3; int[][] table = new array[ARRAY_SIZE][ ARRAY_SIZE]; ) b) How many elements does the array contain? (3*3=9) c) Use a for statement to initialize each element of the array to the sum of its indices. Assume that the integer variables x and y are declared as control variables. ( for (int x = 0; x < ARRAY_SIZE; x++) for (int y = 0; y < ARRAY_SIZE; y++) { table[x][y] = x+y; } )
7.5 Find and correct the error in each of the following program segments: a) final int ARRAY_SIZE = 5; ARRAY_SIZE = 10; b) Assume int[] b = new int[10]; for (int i = 0; i <= b.length; i++) b[i] = 1; c) Assume int[][] a = {{1, 2}, {3, 4}}; a[1, 1] = 5; Exercises 7.6 Fill in the blanks in each of the following statements: a) One-dimensional array p contains four elements. The names of those elements are p[0], p[1], p[2] and p[3]. b) Naming an array, stating its type and specifying the number of dimensions in the array is called the array declaration. c) In a two-dimensional array, the first index identifies the row of an element and the second index identifies the column of an element. d) An m-by-n array contains m rows, n columns and m*n elements. e) The name of the element in row 3 and column 5 of array d is d[2][4]. 7.7 Determine whether each of the following is true or false. If false, explain why. a) To refer to a particular location or element within an array, we specify the name of the array and the value of the particular element. (F) b) An array declaration reserves space for the array. (T) c) To indicate that 100 locations should be reserved for integer array p, you write the declaration p[100]; (T) d) An application that initializes the elements of a 15-element array to zero must contain at least one for statement. (T) e) An application that totals the elements of a two-dimensional array must contain nested for statements. (T) 7.8 Write Java statements to accomplish each of the following tasks: a) Display the value of element 6 of array f. (System.out.println(f[6]);) b) Initialize each of the five elements of one-dimensional integer array g to 8. ( for (int x = 0; x < g.length; x++) total += g[x]; ) c) Total the 100 elements of floating-point array c. d) Copy 11-element array a into the first portion of array b, which contains 34 elements. e) Determine and display the smallest and largest values contained in 99-element floatingpoint array w. 7.9 Consider a two-by-three integer array t. a) Write a statement that declares and creates t. (int[][] t = new int[2][3]) b) How many rows does t have? (2) c) How many columns does t have? (3) d) How many elements does t have? (6) e) Write access expressions for all the elements in row 1 of t. (for (int[] x: t[1][]) ) f) Write access expressions for all the elements in column 2 of t. (for (int[] x: t[][2])) g) Write a single statement that sets the element of t in row 0 and column 1 to zero. (t[0][1] = 0;) h) Write individual statements to initialize each element of t to zero. (for (int x: t) { x = 0; }) i) Write a nested for statement that initializes each element of t to zero. j) Write a nested for statement that inputs the values for the elements of t from the user. k) Write a series of statements that determines and displays the smallest value in t. l) Write a single printf statement that displays the elements of the first row of t. m) Write a statement that totals the elements of the third column of t. Do not use repetition. n) Write a series of statements that displays the contents of t in tabular format. List the column indices as headings across the top, and list the row indices at the left of each row. 7.10 (Sales Commissions) Use a one-dimensional array to solve the following problem: A company pays its salespeople on a commission basis. The salespeople receive $200 per week plus 9% of their gross sales for that week. For example, a salesperson who grosses $5,000 in sales in a week receives $200 plus 9% of $5,000, or a total of $650. Write an application (using an array of counters) that determines how many of the salespeople earned salaries in each of the following ranges (assume that each salesperson’s salary is truncated to an integer amount): a) $200–299 b) $300–399 c) $400–499 d) $500–599 e) $600–699 f) $700–799 g) $800–899 h) $900–999 i) $1,000 and over Summarize the results in tabular format. 7.11 Write statements that perform the following one-dimensional-array operations: a) Set the 10 elements of integer array counts to zero. b) Add one to each of the 15 elements of integer array bonus. c) Display the five values of integer array bestScores in column format. 7.12 (Duplicate Elimination) Use a one-dimensional array to solve the following problem: Write an application that inputs five numbers, each between 10 and 100, inclusive. As each number is read, display it only if it’s not a duplicate of a number already read. Provide for the “worst case,” in which all five numbers are different. Use the smallest possible array to solve this problem. Display the complete set of unique values input after the user enters each new value. 7.13 Label the elements of three-by-five two-dimensional array sales to indicate the order in which they’re set to zero by the following program segment: for (int row = 0; row < sales.length; row++) { for (int col = 0; col < sales[row].length; col++) { sales[row][col] = 0; } } 7.14 (Variable-Length Argument List) Write an application that calculates the product of a series of integers that are passed to method product using a variable-length argument list. Test your method with several calls, each with a different number of arguments. 7.15 (Command-Line Arguments) Rewrite Fig. 7.2 so that the size of the array is specified by the first command-line argument. If no command-line argument is supplied, use 10 as the default size of the array. 7.16 (Using the Enhanced for Statement) Write an application that uses an enhanced for statement to sum the double values passed by the command-line arguments. [Hint: Use the static method parseDouble of class Double to convert a String to a double value.] 7.17 (Dice Rolling) Write an application to simulate the rolling of two dice. The application should use an object of class Random once to roll the first die and again to roll the second die. The sum of the two values should then be calculated. Each die can show an integer value from 1 to 6, so the sum of the values will vary from 2 to 12, with 7 being the most frequent sum, and 2 and 12 the least frequent. Figure 7.28 shows the 36 possible combinations of the two dice. Your application should roll the dice 36,000,000 times. Use a one-dimensional array to tally the number of times each possible sum appears. Display the results in tabular format. 7.18 (Game of Craps) Write an application that runs 1,000,000 games of craps (Fig. 6.8) and answers the following questions: a) How many games are won on the first roll, second roll, …, twentieth roll and after the twentieth roll? b) How many games are lost on the first roll, second roll, …, twentieth roll and after the twentieth roll? c) What are the chances of winning at craps? [Note: You should discover that craps is one of the fairest casino games. What do you suppose this means?] d) What is the average length of a game of craps? e) Do the chances of winning improve with the length of the game? 7.19 (Airline Reservations System) A small airline has just purchased a computer for its new automated reservations system. You’ve been asked to develop the new system. You’re to write an application to assign seats on each flight of the airline’s only plane (capacity: 10 seats). Your application should display the following alternatives: Please type 1 for First Class and Please type 2 for Economy. If the user types 1, your application should assign a seat in the firstclass section (seats 1–5). If the user types 2, your application should assign a seat in the economy section (seats 6–10). Your application should then display a boarding pass indicating the person’s seat number and whether it’s in the first-class or economy section of the plane. Use a one-dimensional array of primitive type boolean to represent the seating chart of the plane. Initialize all the elements of the array to false to indicate that all the seats are empty. As each seat is assigned, set the corresponding element of the array to true to indicate that the seat is no longer available. Your application should never assign a seat that has already been assigned. When the economy section is full, your application should ask the person if it’s acceptable to be placed in the first-class section (and vice versa). If yes, make the appropriate seat assignment. If no, display the message "Next flight leaves in 3 hours." 7.20 (Total Sales) Use a two-dimensional array to solve the following problem: A company has four salespeople (1 to 4) who sell five different products (1 to 5). Once a day, each salesperson passes in a slip for each type of product sold. Each slip contains the following: a) The salesperson number b) The product number c) The total dollar value of that product sold that day Thus, each salesperson passes in between 0 and 5 sales slips per day. Assume that the information from all the slips for last month is available. Write an application that will read all this information for last month’s sales and summarize the total sales by salesperson and by product. All totals should be stored in the two-dimensional array sales. After processing all the information for last month, display the results in tabular format, with each column representing a salesperson and each row representing a particular product. Cross-total each row to get the total sales of each product for last month. Cross-total each column to get the total sales by salesperson for last month. Your output should include these cross-totals to the right of the totaled rows and to the bottom of the totaled columns. 7.21 (Turtle Graphics) The Logo language made the concept of turtle graphics famous. Imagine a mechanical turtle that walks around the room under the control of a Java application. The turtle holds a pen in one of two positions, up or down. While the pen is down, the turtle traces out shapes as it moves, and while the pen is up, the turtle moves about freely without writing anything. In this problem, you’ll simulate the operation of the turtle and create a computerized sketchpad. Use a 20-by-20 array floor that’s initialized to zeros. Read commands from an array that contains them. Keep track of the current position of the turtle at all times and whether the pen is currently up or down. Assume that the turtle always starts at position (0, 0) of the floor with its pen up. The set of turtle commands your application must process are shown in Fig. 7.29.
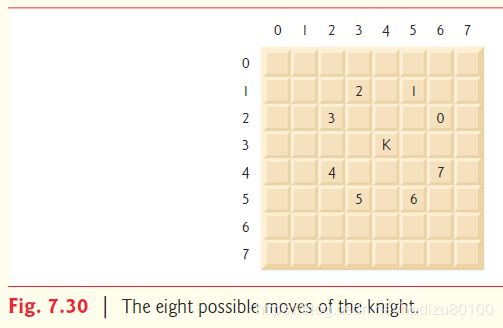
Command -> Meaning 1 -> Pen up 2 -> Pen down 3 -> Turn right 4 -> Turn left 5,10 -> Move forward 10 spaces (replace 10 for a different number of spaces) 6 -> Display the 20-by-20 array 9 -> End of data (sentinel) nd Meaning Suppose that the turtle is somewhere near the center of the floor. The following “program” would draw and display a 12-by-12 square, leaving the pen in the up position: 2 5,12 3 5,12 3 5,12 3 5,12 1 6 9 As the turtle moves with the pen down, set the appropriate elements of array floor to 1s. When the 6 command (display the array) is given, wherever there’s a 1 in the array, display an asterisk or any character you choose. Wherever there’s a 0, display a blank. Write an application to implement the turtle graphics capabilities discussed here. Write several turtle graphics programs to draw interesting shapes. Add other commands to increase the power of your turtle graphics language. 7.22 (Knight’s Tour) An interesting puzzler for chess buffs is the Knight’s Tour problem, originally proposed by the mathematician Euler. Can the knight piece move around an empty chessboard and touch each of the 64 squares once and only once? We study this intriguing problem in depth here. The knight makes only L-shaped moves (two spaces in one direction and one space in a perpendicular direction). Thus, as shown in Fig. 7.30, from a square near the middle of an empty chessboard, the knight (labeled K) can make eight different moves (numbered 0 through 7). a) Draw an eight-by-eight chessboard on a sheet of paper, and attempt a Knight’s Tour by hand. Put a 1 in the starting square, a 2 in the second square, a 3 in the third, and so on. Before starting the tour, estimate how far you think you’ll get, remembering that a full tour consists of 64 moves. How far did you get? Was this close to your estimate? b) Now let’s develop an application that will move the knight around a chessboard. The board is represented by an eight-by-eight two-dimensional array board. Each square is initialized to zero. We describe each of the eight possible moves in terms of its horizontal and vertical components. For example, a move of type 0, as shown in Fig. 7.30, consists of moving two squares horizontally to the right and one square vertically upward. A move of type 2 consists of moving one square horizontally to the left and two squares vertically upward. Horizontal moves to the left and vertical moves upward are indicated with negative numbers. The eight moves may be described by two one-dimensional arrays, horizontal and vertical, as follows: horizontal[0] = 2 vertical[0] = -1 horizontal[1] = 1 vertical[1] = -2 horizontal[2] = -1 vertical[2] = -2 horizontal[3] = -2 vertical[3] = -1 horizontal[4] = -2 vertical[4] = 1 horizontal[5] = -1 vertical[5] = 2 horizontal[6] = 1 vertical[6] = 2 horizontal[7] = 2 vertical[7] = 1 Let the variables currentRow and currentColumn indicate the row and column, respectively, of the knight’s current position. To make a move of type moveNumber, where moveNumber is between 0 and 7, your application should use the statements currentRow += vertical[moveNumber]; currentColumn += horizontal[moveNumber]; Write an application to move the knight around the chessboard. Keep a counter that varies from 1 to 64. Record the latest count in each square the knight moves to. Test each potential move to see if the knight has already visited that square. Test every potential move to ensure that the knight does not land off the chessboard. Run the application. How many moves did the knight make? c) After attempting to write and run a Knight’s Tour application, you’ve probably developed some valuable insights. We’ll use these insights to develop a heuristic (i.e., a common-sense rule) for moving the knight. Heuristics do not guarantee success, but a carefully developed heuristic greatly improves the chance of success. You may have observed that the outer squares are more troublesome than the squares nearer the center of the board. In fact, the most troublesome or inaccessible squares are the four corners. Intuition may suggest that you should attempt to move the knight to the most troublesome squares first and leave open those that are easiest to get to, so that when the board gets congested near the end of the tour, there will be a greater chance of success. We could develop an “accessibility heuristic” by classifying each of the squares according to how accessible it is and always moving the knight (using the knight’s Lshaped moves) to the most inaccessible square. We label a two-dimensional array accessibility with numbers indicating from how many squares each particular square is accessible. On a blank chessboard, each of the 16 squares nearest the center is rated as 8, each corner square is rated as 2, and the other squares have accessibility numbers of 3, 4 or 6 as follows: 2 3 4 4 4 4 3 2 3 4 6 6 6 6 4 3 4 6 8 8 8 8 6 4 4 6 8 8 8 8 6 4 4 6 8 8 8 8 6 4 4 6 8 8 8 8 6 4 3 4 6 6 6 6 4 3 2 3 4 4 4 4 3 2 Write a new version of the Knight’s Tour, using the accessibility heuristic. The knight should always move to the square with the lowest accessibility number. In case of a tie, the knight may move to any of the tied squares. Therefore, the tour may begin in any of the four corners. [Note: As the knight moves around the chessboard, your application should reduce the accessibility numbers as more squares become occupied. In this way, at any given time during the tour, each available square’s accessibility number will remain equal to precisely the number of squares from which that square may be reached.] Run this version of your application. Did you get a full tour? Modify the application to run 64 tours, one starting from each square of the chessboard. How many full tours did you get? d) Write a version of the Knight’s Tour application that, when encountering a tie between two or more squares, decides what square to choose by looking ahead to those squares reachable from the “tied” squares. Your application should move to the tied square for which the next move would arrive at a square with the lowest accessibility number.
|