JPEG算法解密

JPEG算法解密

 by jinchao

 

        图片压缩有多重要，可能很多人可能并没有一个直观上的认识，举个例子，一张800X800大小的普通图片，如果未经压缩，大概在1.7MB左右，这个体积如果存放文本文件的话足够保存一部92万字的鸿篇巨著《红楼梦》，现如今互联网上绝大部分图片都使用了JPEG压缩技术，也就是大家使用的jpg文件，通常JPEG文件相对于原始图像,能够得到1/8的压缩比，如此高的压缩率是如何做到的呢？
        JPEG能够获得如此高的压缩比是因为使用了有损压缩技术，所谓有损压缩，就是把原始数据中不重要的部分去掉，以便可以用更小的体积保存，这个原理其实很常见，比如485194.200000000001这个数，如果我们用485194.2来保存，就是一种“有损”的保存方法，因为小数点后面的那个“0.000000000001”属于不重要的部分，所以可以被忽略掉。JPEG整个压缩过程基本上也是遵循这个步骤：
        1. 把数据分为“重要部分”和“不重要部分”
        2. 滤掉不重要的部分
        3. 保存

步骤一：图像分割

---

        JPEG算法的第一步，图像被分割成大小为8X8的小块，这些小块在整个压缩过程中都是单独被处理的。后面我们会以一张非常经典的图为例，这张图片名字叫做Lenna，据说是世界上第一张JPG图片，这张图片自从诞生之日开始，就和图像处理结下渊源，陪伴了无数理工宅男度过了的一个个不眠之夜，可谓功勋卓著，感兴趣的朋友可以在这里了解到这张图片的故事。

 

步骤二：颜色空间转换RGB->YCbCr

---

        所谓“颜色空间”，是指表达颜色的数学模型，比如我们常见的“RGB”模型，就是把颜色分解成红绿蓝三种分量，这样一张图片就可以分解成三张灰度图，数学表达上，每一个8X8的图案，可以表达成三个8X8的矩阵，其中的数值的范围一般在[0,255]之间。

 

	R		>
	G		>
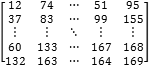	B		>

        不同的颜色模型各有不同的应用场景，例如RGB模型适合于像显示器这样的自发光图案，而在印刷行业，使用油墨打印，图案的颜色是通过在反射光线时产生的，通常使用CMYK模型，而在JPEG压缩算法中，需要把图案转换成为YCbCr模型，这里的Y表示亮度(Luminance)，Cb和Cr分别表示绿色和红色的“色差值”。
        “色差”这个概念起源于电视行业，最早的电视都是黑白的，那时候传输电视信号只需要传输亮度信号，也就是Y信号即可，彩色电视出现之后，人们在Y信号之外增加了两条色差信号以传输颜色信息，这么做的目的是为了兼容黑白电视机，因为黑白电视只需要处理信号中的Y信号即可。
        根据三基色原理，人们发现红绿蓝三种颜色所贡献的亮度是不同的，绿色的“亮度”最大，蓝色最暗，设红色所贡献的亮度的份额为KR，蓝色贡献的份额为KB，那么亮度为

	(1.1)

        根据经验，KR=0.299，KB=0.114，那么

	(1.2)

        蓝色和红色的色差的定义如下

	(1.3)

	(1.4)

        最终可以得到RGB转换为YCbCr的数学公式为

	(1.5)

        YCbCr模型广泛应用在图片和视频的压缩传输中，比如你可以留意一下电视或者DVD后面的接口，就可以发现色差接口。

        这是有道理的，还记得我们在文章开始时提到的有损压缩的基本原理吗？有损压缩首先要做的事情就是“把重要的信息和不重要的信息分开”，YCbCr恰好能做到这一点。对于人眼来说，图像中明暗的变化更容易被感知到，这是由于人眼的构造引起的。视网膜上有两种感光细胞，能够感知亮度变化的视杆细胞，以及能够感知颜色的视锥细胞，由于视杆细胞在数量上远大于视锥细胞，所以我们更容易感知到明暗细节。比如说下面这张图

Y	Cb	Cr

        可以明显看到，亮度图的细节更加丰富。JPEG把图像转换为YCbCr之后，就可以针对数据得重要程度的不同做不同的处理。这就是为什么JPEG使用这种颜色空间的原因。

 

步骤三：离散余弦变换

---

        这次我们来介绍JPEG算法中的核心内容，离散余弦变换（Discrete cosine transform），简称DCT。
        离散余弦变换属于傅里叶变换的另外一种形式，没错，就是大名鼎鼎的傅里叶变换。傅里叶是法国著名的数学家和物理学家，1807年，39岁的傅里叶在他的一篇论文里提出了一个想法，他认为任何周期性的函数，都可以分解为为一系列的三角函数的组合，这个想法一开始并没有得到当时科学界的承认，比如当时著名的数学家拉格朗日提出质疑，三角函数无论如何组合，都无法表达带有“尖角”的函数，一直到1822年拉格朗日死后，傅里叶的想法才正式在他的著作《热的解析理论》一书中正式发表。
        金子总会闪光，傅里叶变换如今广泛应用于数学、物理、信号处理等等领域，变换除了它在数学上的意义外，还有其哲学上的伟大意义，那就是，世上任何复杂的事物，都可以分解为简单的事物的组合，而这个过程只需要借助数学工具就可以了。但是当年拉格朗日的质疑是正确的，三角函数的确无法表达出尖角形状的函数，不过只要三角函数足够多，可以无限逼近最终结果。比如下面这张动图，就动态描述了一个矩形方波，是如何做傅里叶分析的。

 

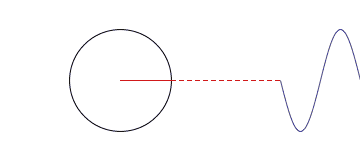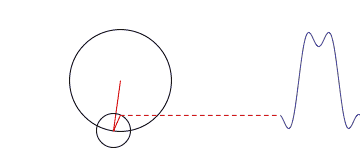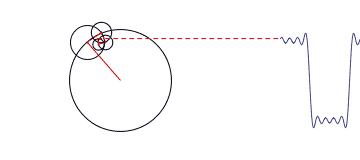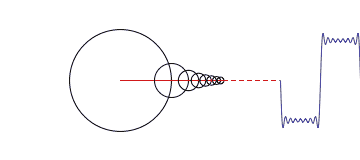        当我们要处理的不再是函数，而是一堆离散的数据时，并且这些数据是对称的话，那么傅里叶变化出来的函数只含有余弦项，这种变换称为离散余弦变换。举个例子，有一组一维数据[x0,x1,x2,…,xn-1],那么可以通过DCT变换得到n个变换级数Fi

	(2.1)

        此时原始数据Xi可以通过离散余弦变换变化的逆变换（IDCT)表达出来

	(2.2)

        也就是说，经过DCT变换，可以把一个数组分解成数个数组的和，如果我们数组视为一个一维矩阵，那么可以把结果看做是一系列矩阵的和

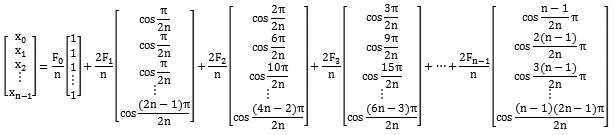	(2.3)

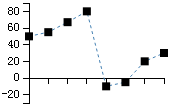
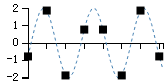
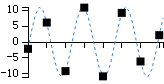
        举个例子，我们有一个长度为8的数字，内容为50,55,67,80,-10,-5,20,30，经过DCT转换，得到8个级数为287.0,106.3,14.2,-110.8,9.2,65.7,-8.2,-43.9，根据公式2.3把这个数组转换为8个新的数组的和，如果我们使用图像来表达的话，就可以发现DCT转换的有趣之处了

[50,55,67,80,-10,-5,20,30]
		数组0
			[35.9,35.9,35.9,35.9,35.9,35.9,35.9,35.9]
		数组1
			[26.0,22.1,14.8,5.2,-5.2,-14.8,-22.1,-26.1]
		数组2
			[3.3,1.4,-1.4,-3.3,-3.3,-1.4,1.4,3.3]
		数组3
			[-23.0,5.4,27.2,15.4,-15.4,-27.2,-5.4,23.0]
		数组4
			[1.6,-1.6,-1.6,1.6,1.6,-1.6,-1.6,1.6]
		数组5
			[9.1,-16.1,3.2,13.6,-13.6,-3.2,16.1,-9.1]
		数组6
			[-0.8,1.9,-1.9,0.8,0.8,-1.9,1.9,-0.8]
		数组7
			[-2.1,6.1,-9.1,10.8,-10.8,9.1,-6.1,2.1]

        奥妙之处在于，经过DCT，数据中隐藏的规律被发掘了出来,杂乱的数据被转换成几个工整变化的数据。DCT转换后的数组中第一个是一个直线数据，因此又被称为“直流数据”，简称DC，后面的数据被称为“交流数据”，简称AC，这个称呼起源于信号分析中的术语。
        在JPEG压缩过程中，经过颜色空间的转换，每一个8X8的图像块，在数据上表现为3个8X8的矩阵，紧接着我们对这三个矩阵做一个二维的DCT转换，二维的DCT转换公式为

	(2.1)

        DCT的威力究竟有多大，我们可以做一个实际的测试，比如一个所有数值都一样的矩阵，经过DCT转换后，将所有级数组合成一个新的矩阵

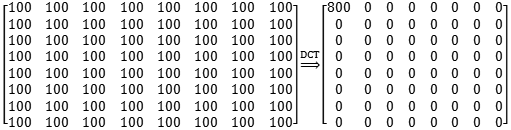        可以看到，经过DCT转换，矩阵的“能量”被全部集中在左上角上的直流分量F(0,0）上，其他位置都变成了0。
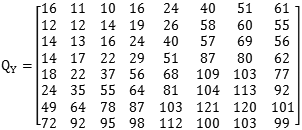
        在实际的JPEG压缩过程中，由于图像本身的连贯性，一个8X8的图像中的数值一般不会出现大的跳跃，经过DCT转换会有类似的效果，左上角的直流分量保存了一个大的数值，其他分量都接近于0，我们以Lenna左上角第一块图像的Y分量为例，经过变换的矩阵为

        可以看到，数据经过DCT变化后，被明显分成了直流分量和交流分量两部分，为后面的进一步压缩起到了充分的铺垫作用，可以说是整个JPEG中最重要的一步，后面我们会介绍数据量化。

 

步骤四：数据量化

---

        经过上一节介绍的离散余弦变换，图像数据虽然已经面目全非，但仍然是处于“可逆”的状态，也就是说我们还没有进入“有损”的那一步。这次我们来玩真的，看一下数据中的细节是如何被滤去的。先来考察一下要对付的问题是什么，经过颜色空间转换和离散余弦变换，每一个8X8的图像块都变成了三个8X8的浮点数矩阵，分别表示Y,Cr,Cb数据，比如以其中某个亮度数据矩阵举例，它的数据如下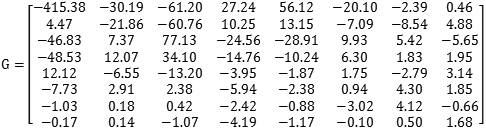

        我们的问题是，在可以损失一部分精度的情况下，如何用更少的空间存储这些浮点数？答案是使用量子化（Quantization），简称量化。“量子”这个概念来自于物理学，意思是说连续的能量可以看做是一个个单元体的组合，看起来高端大气，其实很简单，比如游戏中在处理角色面朝方向时，一般并不是使用0到2π这样的浮点数，而是把方向分成16个区间，用0到16这样的整数来表示，这样只用4个bit就足够了。JPEG提供的量子化算法如下：

 

	(3.1)

        其中G是我们需要处理的图像矩阵，Q称作量化系数矩阵（Quantization matrices），JPEG算法提供了两张标准的量化系数矩阵，分别用于处理亮度数据Y和色差数据Cr以及Cb。

标准亮度量化表	标准色差量化表

        其中round函数是取整函数，但考虑到了四舍五入，也就是说

	(3.2)

        比如上面数据，以左上角的-415.38为例，对应的量子化系数是16，那么round(-415.38/16)=round(-25.96125)=-26。最终得到的量子化后的结果为

        可以看到，一大部分数据变成了0，这非常有利于后面的压缩存储。这两张神奇的量化表也是有讲究的，还记得我们在第一节中所讲的有损压缩的基本原理吗，有损压缩就是把数据中重要的数据和不重要的数据分开，然后分别处理。DCT系数矩阵中的不同位置的值代表了图像数据中不同频率的分量，这两张表中的数据时人们根据人眼对不不同频率的敏感程度的差别所积累下的经验制定的，一般来说人眼对于低频的分量必高频分量更加敏感，所以两张量化系数矩阵左上角的数值明显小于右下角区域。在实际的压缩过程中，还可以根据需要在这些系数的基础上再乘以一个系数，以使更多或更少的数据变成0，我们平时使用的图像处理软件在生成jpg文件时，在控制压缩质量的时候，就是控制的这个系数。
        在进入下一节之前，矩阵的量化还有最后一步要做，就是把量化后的二维矩阵转变成一个一维数组，以方便后面的霍夫曼压缩，但在做这个顺序转换时，需要按照一个特定的取值顺序。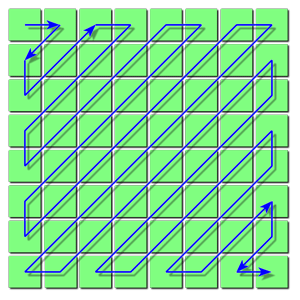

        这么做的目的只有一个，就是尽可能把0放在一起，由于0大部分集中在右下角，所以才去这种由左上角到右下角的顺序，经过这种顺序变换，最终矩阵变成一个整数数组

-26,-3,0,-3,-2,-6,2,-4,1,-3,0,1,5,,1,2,-1,1,-1,2,0,0,0,0,0,-1,-1,0,0,0,0,…,0,0

        后面的工作就是对这个数组进行再一次的哈夫曼压缩，已得到最终的压缩数据。

 

步骤五：哈弗曼编码

---

        JPEG压缩的最后一步是对数据进行哈弗曼编码(Huffman coding)，哈弗曼几乎是所有压缩算法的基础，它的基本原理是根据数据中元素的使用频率，调整元素的编码长度，以得到更高的压缩比。
        举个例子，比如下面这段数据

 

“AABCBABBCDBBDDBAABDBBDABBBBDDEDBD”

        这段数据里面包含了33个字符，每种字符出现的次数统计如下

字符	A	B	C	D	E
次数	6	15	2	9	1

        如果我们用我们常见的定长编码，每个字符都是3个bit。

字符	A	B	C	D	E
编码	001	010	011	100	101

        那么这段文字共需要3*33 = 99个bit来保存，但如果我们根据字符出现的概率，使用如下的编码

字符	A	B	C	D	E
编码	110	0	1110	10	1111

        那么这段文字共需要3*6 + 1*15 + 4*2 + 2*9 + 4*1 = 63个bit来保存，压缩比为63%，哈弗曼编码一般都是使用二叉树来生成的，这样得到的编码符合前缀规则，也就是较短的编码不能够是较长编码的前缀，比如上面这个编码，就是由下面的这颗二叉树生成的。

        我们回到JPEG压缩上，回顾上一节的内容，经过数据量化，我们现在要处理的数据是一串一维数组，举例如下：

①原始数据	35,7,0,0,0,-6,-2,0,0,-9,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,8,0,0,0,…,0

        在实际的压缩过程中，数据中的0出现的概率非常高，所以首先要做的事情，是对其中的0进行处理，把数据中的非零的数据，以及数据前面0的个数作为一个处理单元。

①原始数据	35,7,0,0,0,-6,-2,0,0,-9,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,8,0,0,0,…,0
②RLE编码	35	7	0,0,0,-6	-2	0,0,-9	0,0,…,0,8	0,0,…,0

        如果其中某个单元的0的个数超过16，则需要分成每16个一组，如果最后一个单元全都是0，则使用特殊字符“EOB”表示，EOB意思就是“后面的数据全都是0”,

①原始数据	35,7,0,0,0,-6,-2,0,0,-9,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,8,0,0,0,…,0
②RLE编码	35	7	0,0,0,-6	-2	0,0,-9	0,0,…,0,8		0,0,…,0
	35	7	0,0,0,-6	-2	0,0,-9	0,0,…,0	0,0,8	0,0,…,0
	(0,35)	(0,7)	(3,-6)	(0,-2)	(2,-9)	(15,0)	(2,8)	EOB

        其中（15,0）表示16个0，接下来我们要处理的是括号里右面的数字，这个数字的取值范围在-2047~2047之间，JPEG提供了一张标准的码表用于对这些数字编码：

Value		Size	Bits
0		0	–
-1	1	1	0	1
-3,-2	2,3	2	00,01	10,11
-7,-6,-5,-4	4,5,6,7	3	000,001,010,011	100,101,110,111
-15,…,-8	8,…,15	4	0000,…,0111	1000,…,1111
-31,…,-16	16,…,31	5	0 0000,…,0 1111	1 0000,…,1 1111
-63,…,-32	32,…,63	6	00 0000,…	…,11 1111
-127,…,-64	64,…,127	7	000 0000,…	…,111 1111
-255,…,-128	128,…,255	8	0000 0000,…	…,1111 1111
-511,…,-256	256,…,511	9	0 0000 0000,…	…,1 1111 1111
-1023,…,-512	512,…,1023	10	00 0000 0000,…	…,11 1111 1111
-2047,…,-1024	1024,…,2047	11	000 0000 0000,…	…,111 1111 1111

        举例来说，第一个单元中的“35”这个数字，在表中的位置是长度为6的那组，所对应的bit码是“100011”，而“-6”的编码是”001″，由于这种编码附带长度信息，所以我们的数据变成了如下的格式。

①原始数据	35,7,0,0,0,-6,-2,0,0,-9,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,8,0,0,0,…,0
②RLE编码	35	7	0,0,0,-6	-2	0,0,-9	0,0,…,0,8		0,0,…,0
	35	7	0,0,0,-6	-2	0,0,-9	0,0,…,0	0,0,8	0,0,…,0
	(0,35)	(0,7)	(3,-6)	(0,-2)	(2,-9)	(15,0)	(2,8)	EOB
③BIT编码	(0,6, 100011)	(0,3, 111)	(3,3, 001)	(0,2, 01)	(2,4, 0110)	(15,-)	(2,4, 1000)	EOB

        括号中前两个数字分都在0~15之间，所以这两个数可以合并成一个byte，高四位是前面0的个数，后四位是后面数字的位数。

①原始数据	35,7,0,0,0,-6,-2,0,0,-9,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,8,0,0,0,…,0
②RLE编码	35	7	0,0,0,-6	-2	0,0,-9	0,0,…,0,8		0,0,…,0
	35	7	0,0,0,-6	-2	0,0,-9	0,0,…,0	0,0,8	0,0,…,0
	(0,35)	(0,7)	(3,-6)	(0,-2)	(2,-9)	(15,0)	(2,8)	EOB
③BIT编码	(0,6, 100011)	(0,3, 111)	(3,3, 001)	(0,2, 01)	(2,4, 0110)	(15,-)	(2,4, 1000)	EOB
	(0x6,100011)	(0x3,111)	(0x33,001)	(0x2,01)	(0x24,0110)	(0xF0,-)	(0x24,1000)	EOB

        对于括号前面的数字的编码，就要使用到我们提到的哈弗曼编码了，比如下面这张表，就是一张针对数据中的第一个单元，也就是直流(DC)部分的哈弗曼表，由于直流部分没有前置的0，所以取值范围在0~15之间。

Length	Value	Bits
3 bits	04 05 03 02 06 01 00 (EOB)	000 001 010 011 100 101 110
4 bits	07	1110
5 bits	08	1111 0
6 bits	09	1111 10
7 bits	0A	1111 110
8 bits	0B	1111 1110

        举例来说，示例中的DC部分的数据是0x06，对应的二进制编码是“100”，而对于后面的交流部分，取值范围在0~255之间，所以对应的哈弗曼表会更大一些

Length	Value	Bits
2 bits	01 02	00 01
3 bits	03	100
4 bits	00 (EOB) 04 11	1010 1011 1100
5 bits	05 12 21	1101 0 1101 1 1110 0
6 bits	31 41	1110 10 1110 11
…	…	…
12 bits	24 33 62 72	1111 1111 0100 1111 1111 0101 1111 1111 0110 1111 1111 0111
15 bits	82	1111 1111 1000 000
16 bits	09 … FA	1111 1111 1000 0010 … 1111 1111 1111 1110

        这样经过哈弗曼编码，并且序列化后，最终数据成为如下形式

①原始数据	35,7,0,0,0,-6,-2,0,0,-9,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,8,0,0,0,…,0
②RLE编码	35		7		0,0,0,-6		-2		0,0,-9		0,0,…,0,8			0,0,…,0
	35		7		0,0,0,-6		-2		0,0,-9		0,0,…,0	0,0,8		0,0,…,0
	(0,35)		(0,7)		(3,-6)		(0,-2)		(2,-9)		(15,0)	(2,8)		EOB
③BIT编码	(0,6, 100011)		(0,3, 111)		(3,3, 001)		(0,2, 01)		(2,4, 0110)		(15,-)	(2,4, 1000)		EOB
	(0x6,100011)		(0x3,111)		(0x33,001)		(0x2,01)		(0x24,0110)		0xF0	(0x24,1000)		EOB
④哈弗曼编码	100	100011	100	111	1111 1111 0101	001	01	01	1111 1111 0100	0110	1111 1111 001	1111 1111 0100	1000	1010
⑤序列化	100100011100111111111110101001010111111111010001101111111100111111111010010001010
	91 CF FE A5 7F D1 BF CF FA 45

        最终我们使用了10个字节的空间保存了原本长度为64的数组，至此JPEG的主要压缩算法结束，这些数据就是保存在jpg文件中的最终数据。

 

        这个系列的最后，我提供给大家一个简易的jpeg压缩算法的代码，这份代码用C++编写，以开源方式提供，放在了github上，可以到下面这个网址下载

	http://github.com/thejinchao/jpeg_encoder

        使用方法很简单，像下面这样就可以了

#include "jpeg_encoder.h"
 
JpegEncoder encoder;
//输入的文件必须是24bit的bmp文件，尺寸必须是8的倍数
encoder.readFromBMP(inputFileName);
 
//第二个参数在1~199之间，代表文件压缩程度，数字越大，压缩后的文件体积越小
encoder.encodeToJPG(outputFileName, 50);

        这份代码只是为了配合这个系列的文章，所以没有考虑优化，如果你想在实际工程中使用jpeg的压缩算法，还是使用被广泛应用的libjpeg或者OpenJpeg。

 

转载自：

https://thecodeway.com/blog/?p=69

https://thecodeway.com/blog/?p=353

https://thecodeway.com/blog/?p=480

https://thecodeway.com/blog/?p=522

https://thecodeway.com/blog/?p=690

 原作者： jinchao