From DFA to KMP algorithm

From DFA to KMP algorithm

DFA

In the theory of computation, a branch of theoretical computer science, a deterministic finite automaton (DFA)—also known as deterministic finite acceptor (DFA), deterministic finite-state machine (DFSM), or deterministic finite-state automaton (DFSA)—is a finite-state machine that accepts or rejects a given string of symbols, by running through a state sequence uniquely determined by the string. So, the most important in it is State transition.

DFA and String

DFA does not directly represent a state of the string, but represents a state abstracted from the string, this is an important issue that you need to understand.

KMP algorithm Fundamental

Brute-force substring search

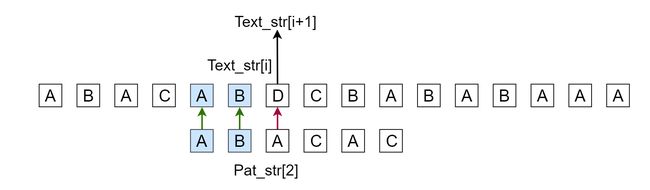
The idea of the KMP algorithm needs to be understood on the basis of violent matching, mainly focusing on the mismatch during the matching process. We assume that there is a text string Text_str and a matching string Pat_str. When using Pat_str to match a text string, Assuming that the part we match is pat_str[0] to pat_str[j], in Text_str, pat_str[i] does not match Text_str[j], then the following situation.

If we directly follow the original method of violence, we will directly move Pat_str one bit back, but while we scan to Text_str[i] we get wrong, this means that we have know the Text_str from Text_str[i-j] to Text_str[i], and we also know what Pat_str stored, so we could know this two parts' relationship, also it must be some complex. So let's consider what the relationship between Text_str[i-j] to Text_str[i] and Pat_str[0] to Pat_str[j].

Backup

In the above problem, we observed that if we return from Text_str[1], we continue to match each time, then it will match at the following position

In the above, the character after Pat_str[2] won't be match. And you will notice that suffixes of Text_str[i] and prefixes of Pat_str[0] is the same, this is the most important problem.

For others conditions of Pat_str and Text_str, they won't have Matching fields of the Prefixes of Pattern_str. The relationship between Text_str[i-j] to Text_str[i] and Pat_str[0] to Pat_str[j] is the prefixes of Pat_str.

DFA of a String Matching

I don't think I could interpreter this problem clearly, so I use a picture of a book to illustrate it, First of all, you must remember what dfa[][] in the blow picture and what dfa[][] save, in the blow picture:

1. The column index of dfa[][] is status of the dfa, it isn't the status of the string but abstracted from the string
2. The row index of dfa[][] is characters in the string,
3. The number save in the dfa[i][A] represent when dfa in status \(i\) , get a character 'A' from string, then next status of dfa[][] is dfa[i][A]

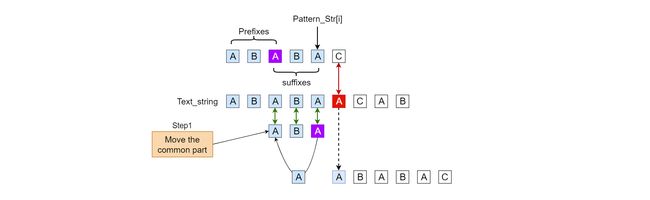
In the above picture , if we get state 6, this means that we match a pattern str in Text_str, so, how can we get the DFA of the Pattern String. Intuitively, we need to find the part with the same prefix and suffix, For example in blow picture:

what we have been matched is 'ABABA', and the common prefix and suffix of this part is 'ABA' and 'ABA'. Actually, the purple char 'A' is where the start of the suffix, and it's most important. In Text_String, the char next to Text_str[j] is actually 'B', so, the dfa's next state is that we have matched four chars. If you understand the common prefix and suffix of the matched part of Text_str, you may also understand code below:

you may need to remember what dfa[][] really is and where is X, in above picture , 'X' is the position of the purple char 'A', it represent the end of the prefix which is the same as the suffix of matched part, and the common length is 'X', in above picture's statue, the X == 2, and j == 4.

dfa[pat.charAt(0)][0] = 1;
for (int X = 0, j = 1; j < M; j++)
{ // Compute dfa[][j].
	for (int c = 0; c < R; c++)
		dfa[c][j] = dfa[c][X];
	dfa[pat.charAt(j)][j] = j+1;
	X = dfa[pat.charAt(j)][X];
}

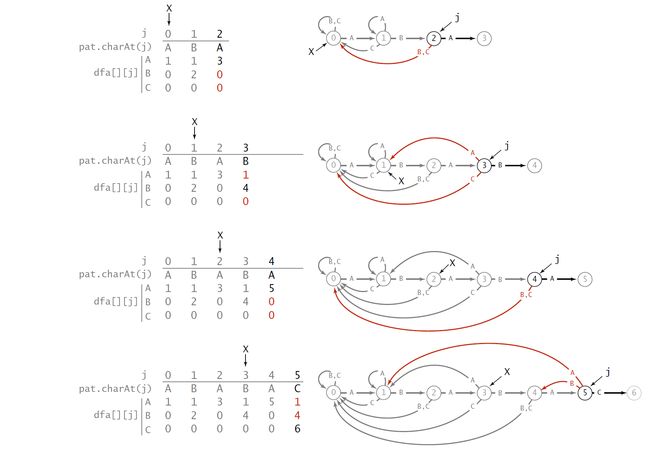
Next , we will interpret the code with more detailed picture with Pattern_str 'ABABAC' and illustrate where the DFA[][] come from:

This step is the first step we construct the DFA[][], and the started X is zero, the next step:

I think I have to illustrate the code in the left:

1. copy dfa[][x] to dfa[][j] , when I first meet this line, I'm also very confused, but when I understand what X is, and this line is a recursive code, I start notice that we can assume the Mismatch condition, If next char mismatch, Intuitively, we only need to move the common prefix to the common suffix part, and then judge the next position, if we use picture condition that we have used, we cloud explain the problem more clearly.

the code actually hide the step1 that we move the prefix, if the mismatch char is 'A', this equivalent to what if 'A' is behind of the purple 'A', where X is.

1. The next line is easily to understand
2. X = dfa[pat.charAt[j][x]], this is also important, this means the common length increase.

The follow-up code is easier to understand, I think you must understand,

Time complexity analysis

when we match a pattern str to a Text_str, we don't back up the Text_str, and the pretreatment time of the pattern text is MR, the R is the alphabet of pattern text. So the the final time is N+MR. The linear-time worst-case guarantee provided by the KMP algorithm is a significant theoretical result. In practice, the speedup over the brute-force method is not often important because few applications involve searching for highly self-repetitive patterns in highly self-repetitive text. Still, the method has the practical advantage that it never backs up in the input.