Monte Carlo Integration

Monte Carlo Integration

Monte Carlo integration uses a different perspective from Quadrature Integration to consider the problem of integration. Quadrature Integration from discrete to continuous, mainly uses the concept of limit convergence and continuous. Monte Carlo integral extended sampling and mathematical expectation of random variables.

Probability Background

Cumulative Distributions and Density Functions

The cumulative distribution function, or CDF, of a random variable \(X\) is the probability that a value chosen from the variable’s distribution is less than or equal to some thresold \(x\):

\[cdf(X) = Pr\{X \leq x \} \]

The corresponding probability density function, or PDF, is the derivative of the CDF:

\[pdf\left( x \right) \ =\ \frac{d}{d_x}cdf\left( x \right) \]

and we can calculate the probility within an interval:

\[Pr\left\{ a\le X\le b \right\} \ =\ \int_a^b{pdf\left( x \right) dx} \]

Expected Values and Variance

The expected value or expectation of a random variable \(Y = f(x)\) over a domain \(\mu(x)\) is defined as:

\[E\left[ Y \right] \ =\ \int_{\mu \left( x \right)}{f\left( x \right) \cdot pdf\left( x \right) d\mu \left( x \right)} \]

while its variance is:

\[\sigma ^2\left[ Y \right] \ =\ E\left[ \left( Y-E\left[ Y \right] \right) ^2 \right] \]

The basic knowledge of probability statistics is this, and we will explain it when we use if have others

TheMonte Carlo Estimator

The Basic Estimator

Monte Carlo integration uses random sampling of a function to numerically compute an estimate of its integral. Suppose that we want to integrate the one-dimensional function \(f (x)\) from \(a\) to \(b\):

\[F\ =\ \int_a^b{f\left( x \right) dx} \]

We can approximate this integral by averaging samples of the function \(f\) at uniform random points within the interval. Given a set of \(N\) uniform random variables \(X_i\in \left[ a,b \right)\) with a corresponding PDF of \(1/(b-a)\), theMonte Carlo estimator for computing \(F\) is:

\[\left\langle F^{N}\right\rangle=(b-a) \frac{1}{N} \sum_{i=0}^{N-1} f\left(X_{i}\right) \tag{1} \]

I think using an example directly, with \(N=4\) and interval \([a,b)\), using uniformly distributed probability density, using random sampling can explain this formula very well.

We use random sampling to get the value of random variable as shown above, as \(f(X_0)\), \(f(X_1)\), \(f(X_2)\), \(f(X_3)\).

Then we use the following picture to simulate integration.

But this integration process is a combination of sampling and statistical calculation of digital characteristics, which is Expected Values. This process is the process of formula (1). If we extend the number 4 to \(N\), we get the result of formula(1).

Expected Value and Convergence

Another question is, in the above question, how do we prove \(\left\langle F^{N}\right\rangle = F\ =\ \int_a^b{f\left( x \right) dx}\) , wo first introducte a Theorem

Law of Large Numbers

Let \(X_1, X_2, \dots\) be i.i.d(independent and identically distributed) with \(E[X_i] = \mu \in R\), \(Var(X_i) = \sigma^2 \in (0, \infty)\) , if, \(\bar{X}_{n}=\frac{1}{n} \sum_{i=1}^{n} X_{i}\) then, \(\bar{X}_{n} \rightarrow \mu\) in \(L^2\) .

we can get a result according to LLN :

\[\operatorname{Pr}\left\{\lim _{N \rightarrow \infty}\left\langle F^{N}\right\rangle=E[\left\langle F^{N}\right\rangle]\right\}=1 \]

and there is another problem is:

\[\begin{aligned} E\left[\left\langle F^{N}\right\rangle\right] &=E\left[(b-a) \frac{1}{N} \sum_{i=0}^{N-1} f\left(X_{i}\right)\right] \\ &=(b-a) \frac{1}{N} \sum_{i=0}^{N-1} E\left[f\left(X_{i}\right)\right] \\ &=(b-a) \frac{1}{N} \sum_{i=0}^{N-1} \int_{a}^{b} f(x) p d f(x) d x \\ &=\frac{1}{N} \sum_{i=0}^{N-1} \int_{a}^{b} f(x) d x \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ since \ \ pdf (x) = 1/(b -a) \\ &=\int_{a}^{b} f(x) d x \\ &=F \end{aligned} \tag{2} \]

Therefore,

\[\operatorname{Pr}\left\{\lim _{N \rightarrow \infty}\left\langle F^{N}\right\rangle=F\right\}=1 \]

Multidimensional Integration

Monte Carlo integration can be generalized to use random variables drawn from arbitrary PDFs and to compute multidimensional integrals, such as:

\[F\ =\ \int_{\mu \left( x \right)}{f\left( x \right) d \mu \left( x \right)} \]

with the following modification to Equation (1):

\[\left\langle F^{N}\right\rangle= \frac{1}{N} \sum_{i=0}^{N-1} \frac{f\left(X_{i}\right)}{pdf(X_i)} \tag{3} \]

It is similarly easy to show that this generalized estimator also has the correct expected value:

\[\begin{aligned} E\left[\left\langle F^{N}\right\rangle\right] &=E\left[\frac{1}{N} \sum_{i=0}^{N-1} \frac{f\left(X_{i}\right)}{\operatorname{pdf}\left(X_{i}\right)}\right] \\ &=\frac{1}{N} \sum_{i=0}^{N-1} E\left[\frac{f\left(X_{i}\right)}{\operatorname{pdf}\left(X_{i}\right)}\right] \\ &=\frac{1}{N} \sum_{i=0}^{N-1} \int_{\Omega} \frac{f(x)}{p d f(x)} p d f(x) d x \\ &=\frac{1}{N} \sum_{i=0}^{N-1} \int_{\Omega} f(x) d x \\ &=\int_{\Omega} f(x) | d x \\ &=F \end{aligned} \]

In addition to the convergence rate, a secondary benefit ofMonte Carlo integration over traditional numerical integration techniques is the ease of extending it to multiple dimensions. Deterministic quadrature techniques require using \(N^d\) samples for a d-dimensional integral. In contrast,Monte Carlo techniques provide the freedom of choosing any arbitrary number of samples. That means, we don't need to calculate every d-dimensional cube very clearly.

Sources of Variance

For the Variance of The Basic Estimator of Monte Carlo integration, Since the samples in Monte Carlo Method are independent, using Equation the variance of \(\left\langle F^{N}\right\rangle\) can be simplified to:

\[\begin{aligned} \sigma^{2}\left[\left\langle F^{N}\right\rangle\right] &=\sigma^{2}\left[\frac{1}{N} \sum_{i=0}^{N-1} \frac{f\left(X_{i}\right)}{p d f\left(X_{i}\right)}\right] \\ &=\frac{1}{N^{2}} \sum_{i=0}^{N-1} \sigma^{2}\left[\frac{f\left(X_{i}\right)}{p d f\left(X_{i}\right)}\right] \\ &=\frac{1}{N^{2}} \sum_{i=0}^{N-1} \sigma^{2}\left[Y_{i}\right] \\ &=\frac{1}{N} \sigma^{2}[Y] \end{aligned} \tag{4} \]

and hence:

\[\sigma\left[\left\langle F^{N}\right\rangle\right]=\frac{1}{\sqrt{N}} \sigma[Y] \tag{5} \]

where \(Y_i = f(X_i) / pdf(X_i)\) and \(Y\) represents the evaluation of any specific \(Y_i\) , This derivation proves that the standard deviation converges with \(O(\sqrt N)\) . Moreover, this expression shows that by reducing the variance of each \(Y_i\) we can reducet he overall variance of \(\left\langle F^{N}\right\rangle\).

Variance Reduction

Earlier we calculated the variance of the Monte Carlo method to calculate the integral. This variance comes from the difference between the probability density function(PDF) that the sample conforms to and the integral function we seek. From the perspective of mathematical expectations, Monte Carlo integration can converge to traditional numerical integration, and the variance reflects the volatility of the sample. This means that if the sampling process is more similar to the integrand, the smaller the variance.

Importance Sampling

To demonstrate the effect of importance sampling, consider a PDF which is exactly proportional to the function being integrated, \(pdf(x) = cf(x)\) for some normalization constant \(c\). Since \(c\) is a constant, if we apply this PDF to theMonte Carlo estimator in Equation(3) , each sample \(X_i\) would have the same value.

\[Y_{i}=\frac{f\left(X_{i}\right)}{p d f\left(X_{i}\right)}=\frac{f\left(X_{i}\right)}{c f\left(X_{i}\right)}=\frac{1}{c} \tag{6} \]

Since the PDF must integrate to one, it is easy to derive the value of \(c\):

\[c=\frac{1}{\int{f\left( x \right) dx}} \]

However, \(C\) is actually what we want to know, so, This best case is therefore not a realistic situation.

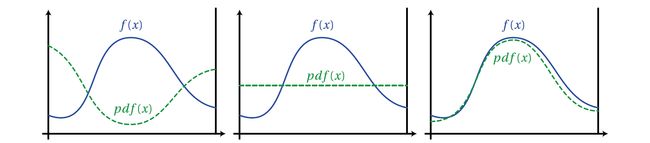
and we could use a figure to express the importance between the \(pdf(x)\) and \(f(x)\)

Comparison of three probability density functions. The PDF on the right provides variance reduction over the uniform PDF in the center. However, using the PDF on the left would significantly increase variance over simple uniform sampling. This is also easy to explain. For example, in the figure on the left, the probability of the distribution of \(X_i\) obtained by using the density function \(pdf(x)\) at both ends is greater than the probability of being distributed in the middle.

Importance Sampling Complex Functions

Most of the time, the integrand \(f (x)\) is very complicated, and we cannot guess its full behavior ahead of time. However, we may know something about its general structure. For instance, the integrand function \(f (x)\) may in fact be the combination of more than one function, e.g., \(f(x) = g(x)h(x)\) . In these situations, it may not be possible to create a PDF exactly proportional to \(f (x)\), but, if we know one of the functions in advance, we may be able to construct a PDF proportional to a portion of \(f (x)\), e.g., \(pdf_g (x) \propto g (x)\). In this situation, the Monte Carlo estimator simplifies to:

\[\begin{aligned} \left\langle F^{N}\right\rangle &=\frac{1}{N} \sum_{i=0}^{N-1} \frac{f\left(X_{i}\right)}{p d f_{g}\left(X_{i}\right)} \\ &=\frac{1}{N} \sum_{i=0}^{N-1} \frac{g\left(X_{i}\right) h\left(X_{i}\right)}{c g\left(X_{i}\right)} \\ &=\frac{1}{c N} \sum_{i=0}^{N-1} h\left(X_{i}\right) \end{aligned} \tag{7} \]

The above is a method to simplify the integration function \(f\). In addition, the operation of \(f\) can also be operated by polynomials, for example：Control variates is another variance-reduction technique which relies on some prior knowledge of the behavior of \(f\) . The idea behind control variates is to find a function g which can be analytically integrated and subtract it from the integral of \(f\):

\[\begin{aligned} F &=\int_{a}^{b} f(x) d x \\ &=\int_{a}^{b} f(x)-g(x) d x+\int_{a}^{b} g(x) d x \\ &=\int_{a}^{b} f(x)-g(x) d x+G \end{aligned} \tag{8} \]

We can then applyMonte Carlo integration to the modified integrand \(f (x)-g (x)\):

\[\left\langle F_{c}^{N}\right\rangle=\left(\frac{1}{N} \sum_{i=0}^{N-1} \frac{f\left(X_{i}\right)-g\left(X_{i}\right)}{p d f\left(X_{i}\right)}\right)+G \\ = \left\langle F_{c}^{N}\right\rangle + G - \left\langle G^{N}\right\rangle \tag{9} \]

The ultimate goal of sampling in different ways is to make the variance of the Monte Carlo method small enough, In order to achieve this, we can operate in addition to the probability density function used for sampling, and also the sampling interval. Stratified Sampling is the principle used.

Stratified Sampling

Stratified sampling works by splitting up the original integral into a sum of integrals over sub-domains. In its simplest form, stratified sampling divides the domain \([a,b]\) into \(N\) sub-domains (or interval) and places a random sample within each of these intervals. If using a uniform PDF, with \(\xi _i\in \left[ 0,1 \right)\) , this can be expressed as:

\[\begin{aligned} \left\langle F_{s}^{N}\right\rangle &=\frac{(b-a)}{N} \sum_{i=0}^{N-1} f\left(X_{i}\right) \\ &=\frac{(b-a)}{N} \sum_{i=0}^{N-1} f\left(a+\frac{i+\xi_{i}}{N}(b-a)\right) \\ &=\frac{(b-a)}{N} \sum_{i=0}^{N-1} f\left(a+\xi_{i}^{N}(b-a)\right) \end{aligned} \tag{10} \]

This method changes the sampling interval on the basis of the basic Monte Carlo method to make the sampling more uniform. The probability density function of the sampling used in each interval is still uniformly distributed.

Most of the time, stratification can be added by simply replacing a canonical random number \(\xi _i\in \left[ 0,1 \right)\) with a sequence of stratified random numbers in the same range \(\xi _{i}^{N}=\frac{i+\xi _i}{N}\).

Comparison to Deterministic Quadrature

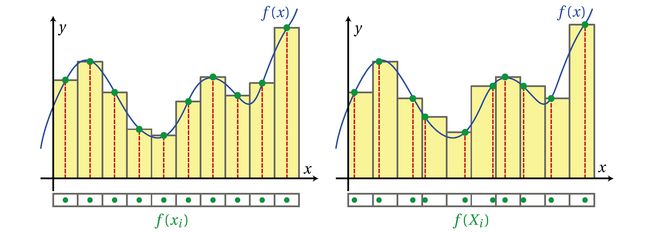
Stratified sampling incorporates ideas from deterministic quadrature, while still retaining the statistical properties ofMonte Carlo integration. It is informative to compare Equation 10 to a simple Riemann summation of the integral:

\[\begin{aligned} F=\int_{a}^{b} f(x) d x & \approx \sum_{i=0}^{N-1} f\left(x_{i}\right) \Delta x \\ & \approx \sum_{i=0}^{N-1} f\left(a+\frac{i}{N}(b-a)\right) \frac{(b-a)}{N} \\ & \approx \frac{(b-a)}{N} \sum_{i=0}^{N-1} f\left(a+\frac{i}{N}(b-a)\right) \end{aligned} \tag{11} \]

The Stratified samplingprocess can also be seen as Monte Carlo integration for each interval.

Deterministic quadrature techniques such as a Riemann summation (left) sample the function at regular intervals. Conceptually, stratifiedMonte Carlo integration (right) performs a very similar summation, but instead evaluates the function at a random location within each of the strata.