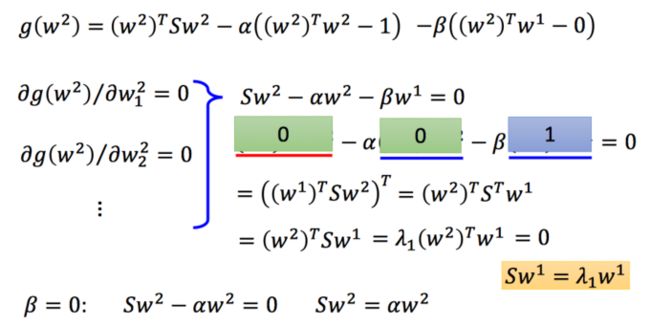PCA大法好！

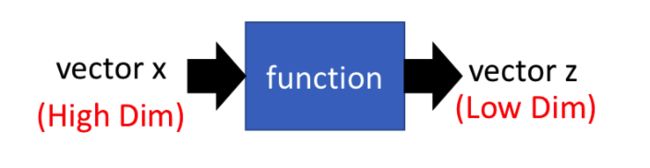
1. 降维

x x 和 z z 之间的关系是线性变换，所以可以看成： z=Wx z = W x ，那么如何找出 W W ？

2. PCA

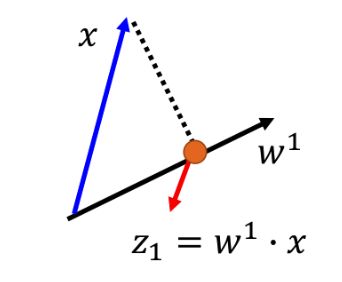
如果假设 z z 只是1维的话，则 z1=w1⋅x z 1 = w 1 ⋅ x ，所以 w1 w 1 是 W W 的第一行，假设 w1 w 1 的长度为1， x x 是空间中的一个点， w1⋅x w 1 ⋅ x 可以看成 x x 在 w1 w 1 上的投影，如下图：

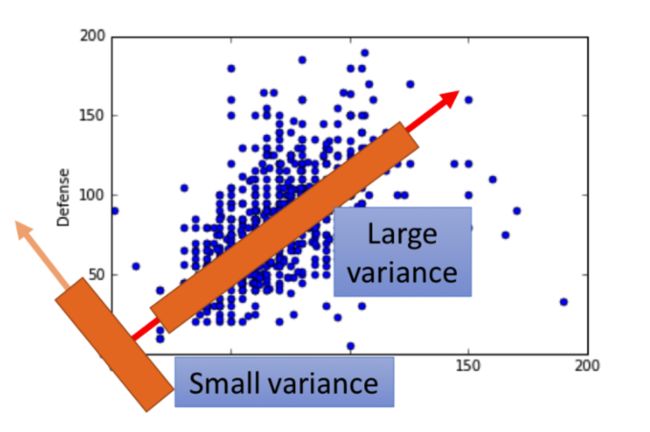
所以我们的目标是，把dataset里面所有的 xi x i 都投影到 w1 w 1 上，得到对应的a set of z1 z 1 。这个 w1 w 1 的选择可以有多种（下图中的两个箭头方向），我们的目标是，希望投影之后的data，不要都挤在一起，还是能有区分度，所以我们希望 z1 z 1 的方差（Variance）越大越好。下图中的橘色方框表示在该方向的 z1 z 1 的分布，可以看出，红色箭头代表的 w1 w 1 方向上的投影分布会更大一些，即方差更大。

所以我们要maximize的目标是：

Var(z1)=∑z1(z1−z1¯)2 V a r ( z 1 ) = ∑ z 1 ( z 1 − z 1 ¯ ) 2 ， ||w1||2=1 | | w 1 | | 2 = 1 。

如果现在 z z 变为两维，假设我们通过上述方法已经找到了 w1 w 1 ，怎么找 w2 w 2 呢？很明显也是相似的思路，希望data在 w2 w 2 上的投影Variance越大越好，但是如果我们单纯去maximize Var(z2)=∑z2(z2−z2¯)2 V a r ( z 2 ) = ∑ z 2 ( z 2 − z 2 ¯ ) 2 ，那找出来的还是 w1 w 1 ，所以还要加上一个限制条件： w1⋅w2=0 w 1 ⋅ w 2 = 0 ，即希望 w1 w 1 和 w2 w 2 是orthogonal的，因此最后找出来的 W W 是orthogonal matrix。

2.1 w1 w 1 如何求解？

Var(z1)=(w1)TCov(x)w1 V a r ( z 1 ) = ( w 1 ) T C o v ( x ) w 1

推导如下：

所以我们的目标变为：maximize (w1)TSw1 ( w 1 ) T S w 1 ，加上约束 ||w1||2=(w1)Tw1=1 | | w 1 | | 2 = ( w 1 ) T w 1 = 1 。

因为 S S 是协方差矩阵，所以 S S 是对称+半正定的，所以 S S 的特征值都是非负的。

结论： w1 w 1 is the eigenvector of the covariance matrix S S corresponding to the largest eigenvalue λ1 λ 1 .

推导如下，利用拉格朗日乘子法求解，得到 Sw1=αw1 S w 1 = α w 1 ，可见 w1 w 1 是 S S 的一个特征向量（eigenvector），而那么多eigenvector选哪一个呢？因为我们的目标是要maximize (w1)TSw1 ( w 1 ) T S w 1 ，代入 Sw1=αw1 S w 1 = α w 1 ，得到 (w1)TSw1=α ( w 1 ) T S w 1 = α ，所以目标就是maximize w1 w 1 对应的这个特征值 α α ！那直接取最大的特征值就好了，即 w1 w 1 是最大的eigenvalue对应的eigenvector。

2.2 w2 w 2 如何求解？

要求解 w2 w 2 ，我们的目标是maximize (w2)TSw2 ( w 2 ) T S w 2 ，同时有两个约束： (w2)Tw2=1 ( w 2 ) T w 2 = 1 ， (w2)Tw1=0 ( w 2 ) T w 1 = 0 。

结论是：

w2 w 2 是协方差矩阵 S S 第二大的eigenvalue对应的eigenvector。

证明：

Sw2−αw2−βw1=0 S w 2 − α w 2 − β w 1 = 0 ，两边同时乘上 (w1)T ( w 1 ) T ，得到 (w1)TSw2−α(w1)Tw2−β(w1)Tw1=0 ( w 1 ) T S w 2 − α ( w 1 ) T w 2 − β ( w 1 ) T w 1 = 0 ，化简得到： β=0 β = 0 。带回原式，有： Sw2−αw2=0 S w 2 − α w 2 = 0 。所以 w2 w 2 可以选 S S 的第二大的eigenvalue对应的eigenvector，这样它和 w1 w 1 刚好是orthogonal的（因为 S S 是对称阵），同时满足maximize的条件。

2.3 PCA维数如何选择？

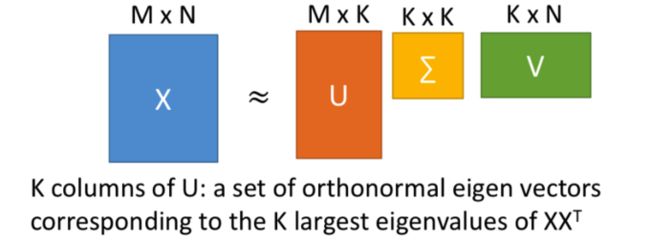
对 X X 做SVD后得到的矩阵 U U 就是对应PCA的解。

计算每个eigenvector对应的eigenvalue的ratio：

λi∑iλi λ i ∑ i λ i

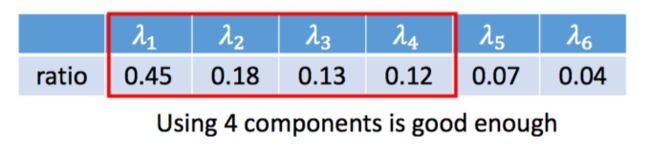
因为eigenvalue代表在对应的eigenvector上降维后的方差。（？）

2.4 PCA的缺点

• 对带类别的数据集降维效果不一定好

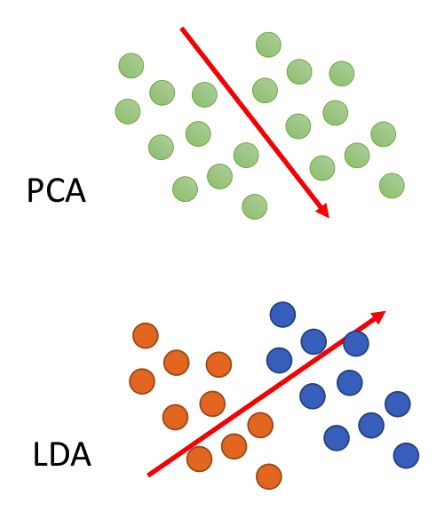
如图，如果让PCA来对图中的两个类别（橘色和蓝色）的data降维，它可能会依据投影后方差最大的原则选择向右下方的这个投影方向，但是在这个方向上投影会将橘色和蓝色两个不同类别的data都混在一起，而基于有监督学习的线性判别器（LDA）可以较好的解决这个问题。

• 可解释性不高
  PCA最后得到的不是原始特征，而是原始特征经过坐标系变换后的结果，是原始特征的一个加权。

2.5 代码

pca = PCA(n_components=2, whiten=True, random_state=0)
    x = pca.fit_transform(x)
    print '各方向方差：', pca.explained_variance_
    print '方差所占比例：', pca.explained_variance_ratio_
    print x[:5]