傅里叶变换求解 KdV 方程
KdV方程的出处: Dr. D. J. Korteweg & Dr. G. de Vries (1895) XLI. On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves, The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 39:240, 422-443, DOI: 10.1080/14786449508620739
@article{doi:10.1080/14786449508620739,
author = { Dr. D. J. Korteweg and Dr. G. de Vries },
title = {XLI. On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves},
journal = {The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science},
volume = {39},
number = {240},
pages = {422-443},
year = {1895},
publisher = {Taylor & Francis},
doi = {10.1080/14786449508620739},
URL = {https://doi.org/10.1080/14786449508620739},
eprint = {https://doi.org/10.1080/14786449508620739},
}
∂ u ∂ t + u ∂ u ∂ x + ∂ 3 u ∂ x 3 = 0 , \frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + \frac{\partial^3 u}{\partial x^3} = 0, ∂t∂u+u∂x∂u+∂x3∂3u=0,
瞬态波形
当固定 t t t 时, ∂ u ∂ t = 0 \frac{\partial u}{\partial t} = 0 ∂t∂u=0. 得
u ∂ u ∂ x + ∂ 3 u ∂ x 3 = 0 , (1) u\frac{\partial u}{\partial x} + \frac{\partial^3 u}{\partial x^3} = 0, \tag{1} u∂x∂u+∂x3∂3u=0,(1)
对(1)关于 x x x积分,或者
∂ ∂ x ( 1 2 u 2 + ∂ 2 u ∂ x 2 ) = 0 , \frac{\partial }{\partial x}\left( \frac{1}{2}u^2+ \frac{\partial^2 u}{\partial x^2} \right)= 0, ∂x∂(21u2+∂x2∂2u)=0,
得
c + 1 2 u 2 + ∂ 2 u ∂ x 2 = 0 , (2) c + \frac{1}{2}u^2+ \frac{\partial^2 u}{\partial x^2} = 0, \tag{2} c+21u2+∂x2∂2u=0,(2)
对(2)关于 u u u积分,得
c 1 u + 1 6 u 3 + ∫ ∂ 2 u ∂ x 2 d u = c 2 c_1u + \frac{1}{6}u^3+ \int{\frac{\partial^2 u}{\partial x^2} du} = c_2 c1u+61u3+∫∂x2∂2udu=c2 c 1 u + 1 6 u 3 + ∫ ∂ 2 u ∂ x 2 ∂ u ∂ x d x = c 2 c_1u + \frac{1}{6}u^3+ \int{\frac{\partial^2 u}{\partial x^2} \frac{\partial u}{\partial x}dx} = c_2 c1u+61u3+∫∂x2∂2u∂x∂udx=c2 c 1 u + 1 6 u 3 + ∫ ∂ u ∂ x d ∂ u ∂ x = c 2 c_1u + \frac{1}{6}u^3+ \int{ \frac{\partial u}{\partial x}d\frac{\partial u}{\partial x}} = c_2 c1u+61u3+∫∂x∂ud∂x∂u=c2 c 1 u + 1 6 u 3 + 1 2 ( ∂ u ∂ x ) 2 = c 2 , (3) c_1u + \frac{1}{6}u^3+ \frac{1}{2} \left(\frac{\partial u}{\partial x}\right)^2 = c_2, \tag{3} c1u+61u3+21(∂x∂u)2=c2,(3)
情形一
假设无穷远处, x → ∞ x\to \infty x→∞,
u = 0 , ∂ u ∂ x = 0 , ∂ 2 u ∂ x 2 = 0 u=0, \frac{\partial u}{\partial x} = 0, \frac{\partial^2 u}{\partial x^2} = 0 u=0,∂x∂u=0,∂x2∂2u=0
由(2)(3)可知: c 1 = c 2 = 0 c_1 = c_2 = 0 c1=c2=0. 所以(3)改写为:
∂ u ∂ x = ± − 1 3 u 3 = ± u − 1 3 u \frac{\partial u}{\partial x} = \pm\sqrt{- \frac{1}{3}u^3} = \pm u\sqrt{- \frac{1}{3}u} ∂x∂u=±−31u3=±u−31u
情形二
周期边界条件,blablabla
用傅里叶变换求解偏微分方程
傅里叶变换可以将 PDE 转换成 ODE,即:将 u ( x , t ) u(x,t) u(x,t) 在空间上做傅里叶展开,关于 x x x的微分项全部变成代数乘除,只剩下时间上的微分,所以可以用 ODE 的解法在频域上求解 u ^ k ( t ) \hat{u}_k(t) u^k(t).
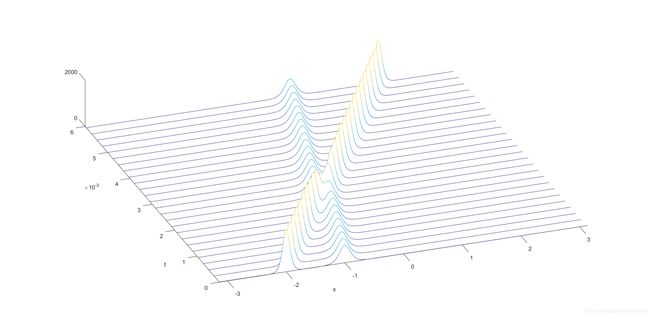
matlab 仿真
% Solve KdV eq. u_t + uu_x + u_xxx = 0 on [-pi,pi] by
% FFT with integrating factor v = exp(-ik^3t)*u-hat.
% Set up grid and two-solution initial data:
N = 256;
dt = .4/N^2;
x = (2*pi/N)*(-N/2:N/2-1)';
A = 25;
B = 16;
clf, drawnow
u = 3*A^2*sech(.5*(A*(x+2))).^2 + 3*B^2*sech(.5*(B*(x+1))).^2;
v = fft(u);
k = [0:N/2-1 0 -N/2+1:-1]';
ik3 = 1i*k.^3;
% Solve PDE and plot results:
tmax = 0.006;
nplt = floor((tmax/25)/dt);
nmax = round(tmax/dt);
udata = u;
tdata = 0;
h = waitbar(0,'please wait...');
for n = 1:nmax
t = n*dt;
g = -.5i*dt*k;
E = exp(dt*ik3/2);
E2 = E.^2;
a = g.*fft(real( ifft( v ) ).^2); % 这里的 abcd 是4阶龙哥库塔积分步骤
b = g.*fft(real( ifft(E.*(v+a/2)) ).^2);
c = g.*fft(real( ifft(E.*v + b/2) ).^2);
d = g.*fft(real( ifft(E2.*v+E.*c) ).^2);
v = E2.*v + (E2.*a + 2*E.*(b+c) +d)/6;
if mod(n,nplt) == 0
u = real(ifft(v));
waitbar(n/nmax)
udata = [udata u];
tdata = [tdata t]
end
end
waterfall(x,tdata,udata'), color([0 1 0]), view(-20,25)
xlabel x, ylabel t, axis([-pi pi 0 tmax 0 2000]), grid off
set(gca,'ztick',[0 2000]), close(h), pbaspect([1 1 .13])