机器学习之逻辑回归 Logistic Regression（一）

参考 http://blog.csdn.net/han_xiaoyang/article/details/49123419

一、逻辑回归

        逻辑回归是一个应用非常广泛的机器学习分类算法，它将数据拟合到一个logit函数中，从而完成对事件发生概率的预测。线性回归对连续值进行预测，现实生活中常见的另一类问题是分类问题。最直接的想法是，用线性回归预测出连续值结果，根据结果设定一个阈值进行分类。但很多实际的情况下，需要学习的分类数据并没有那么精准，线性回归+阈值的方式很难完成一个鲁棒性很好的分类器。

        在这样的场景下，逻辑回归诞生了。它的核心思想是，如果线性回归的结果输出是一个连续值，而值的范围是无法限定的，那是否可以把这个结果映射为(0, 1)上的概率值，帮助判断结果。sigmoid函数就是这样一个简单的函数：

        从函数图上可以看出，函数y=g(z)在z=0时为1/2，随着z逐渐变小，函数值趋于0，z逐渐变大时函数值趋于1。如果定义线性回归的预测函数为，那么逻辑回归的输出，其中y=g(z)正是上述sigmoid函数。
        直观地在二维空间理解逻辑回归，sigmoid函数的特性使得判定的阈值能够映射为平面的一条判定边界，当然随着特征的复杂化，判定边界可能是多种多样的样貌，但是它能够较好地把两类样本点分隔开，解决分类问题。
        求解逻辑回归参数的传统方法是梯度下降，构造为凸函数的代价函数后，每次沿着偏导方向（下降速度最快方向）迈进一小部分，直至N次迭代后到达最低点。

二、决策边界

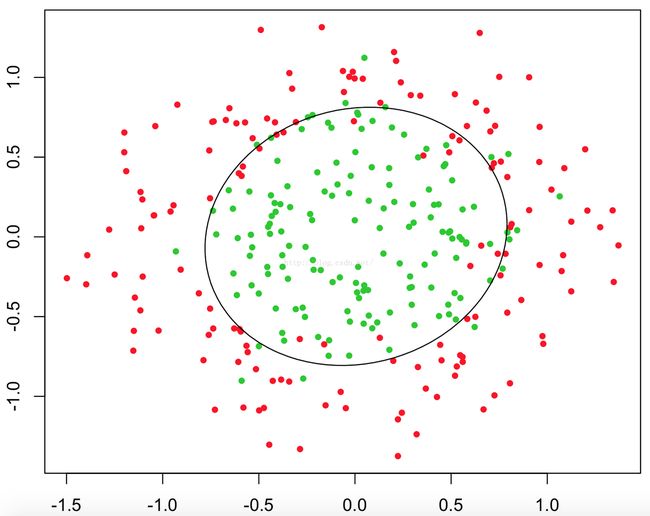
        逻辑回归之所以能够解决分类问题，需要一个决策边界，决策边界可以理解为用以对不同类别数据分割的边界，边界两旁是不同类别的数据。例如下图中圆将红绿样本点分割开来，就是决策边界。

        逻辑回归如何根据样本点获得决策边界呢？回到sigmoid函数，当g(z)>0.5时，z>0。，此时意味着预估y=1。所以认为是一个决策边界，当它大于或小于0时，逻辑回归模型分别预测不同的分类结果。只要g(z)中z设计足够合理，就能在不同情形下拟合出不同的决策边界，从而把不同的样本点分隔开来。

三、损失函数和梯度下降

        损失函数是衡量在一组参数下预估结果和实际结果差距的函数，我们希望损失函数是一个凸函数，这样求得局部最小值就是全局最小值。逻辑回归的损失函数：

四、数学视角解读logit和sigmoid函数

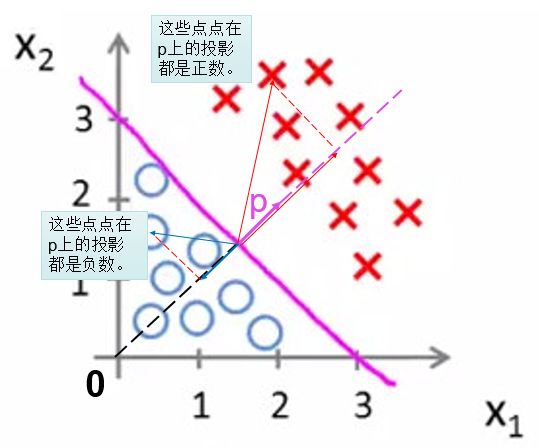
        假设二维平面中有两群点，希望找出一条分离边界，将这两群点分开。假设这两类是线性可分的，即可以找到一条最佳的直线将两类点分开。如何依靠现有点的坐标x(X1, X2)和标签y，找出分界线的方程呢？
        假设已经找到了这条线 ，那么两类点在法向量p上的投影值正负号不同，一类点的投影全是正数，另一类全是负数，这条性质可以用来区分点的不同类别。将法向量p平移到原点得到p’，坐标为 ，点x(X1, X2)到p’的投影就是 ，再加上 ，就是 ，就是逻辑回归函数 括号中的部分。令 ，就可以根据z的正负号来判断点x的类别了。

        z的变化范围是正负无穷大，如果z大于0，则点x属于y=1类，z的值越大，说明它距离分界线越远，更可能属于y=1类。点x属于y=1类的概率P(y=1|x)，简写为P。设z=log⁡(P/(1-P))，这个函数在区间(0, 1)中可正可负，单调变化，并在1/2时刚好为0，可以将z理解为x属于y=1类的概率P经过某种变换后对应的值，z=log⁡(P/(1-P))反过来可以得到，这两个函数就是logit函数和sigmoid函数。
        在概率理论中，Q=P/(1-P)的意义叫做赔率(odds)。赔率也叫发生比，是事件发生和不发生的概率比。而z= log(P/(1-P))的意义就是对数赔率或者对数发生比（log-odds）。
        z映射到概率P的拟合方程：

        有了概率P就可以判断点x所属分类，当P>1/2时，判断点x属于y=1,类，当P<1/2时，判断点x属于y=0类。
        回顾推理过程，其实是不断将点x(X1, X2)进行几何坐标变换的过程。
        第一步将分布在整个二维平面的点x(X1, X2)通过线性投影映射到一维直线上成为点x(z)；
        第二步将分布在整个一维直线的点x(z)通过sigmoid函数映射到一维线段(0, 1)中成为点x(g(z))；
        第三步将所有点的坐标通过损失函数统一计算成一个值，如果这是最小值，相应的参数就是我们需要的理想值。