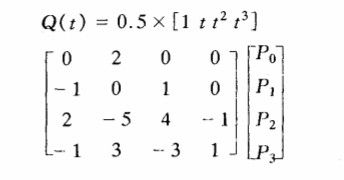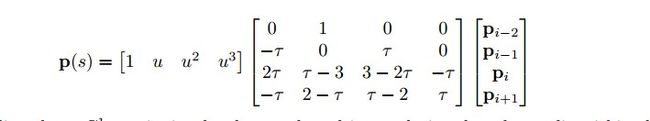meshwarp算法分析
meshwarp是由Smythe90最早提出的,算法中主要由5个操作对象:
1.输入图像
2.source网格
3.目标网格
4.中间图像
5.输出图像
下面首先介绍Smythe使用的两个基本的差值算法,catmull-rom spline算法和FANT‘s resampleing 算法,这两个算法构成了整个Smythe算法的基础。
1.算法1:CATMULL-ROM SPLINE算法。
http://actionsnippet.com/?p=1031 这里有关于Catmull-rom spline的插值算法。
http://www.actionsnippet.com/swfs/catmull_rom.html catmull-rom spline算法(下面简称CR算法)的动画演示
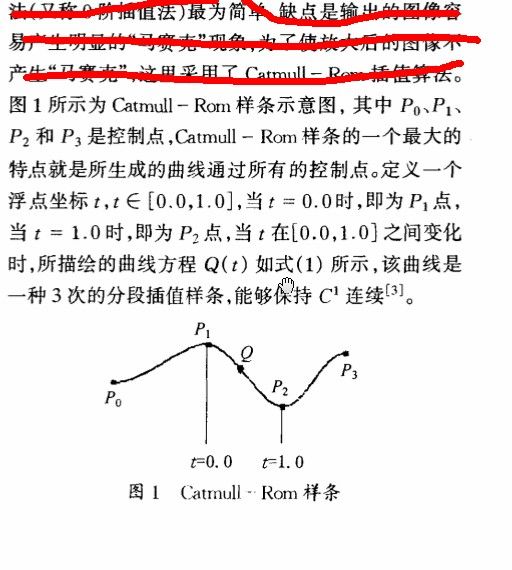
CR算法的公式表达如下图所示:(摘自:http://www.doc88.com/p-84287214027.html 基于Catmull-Rom插值算法的二维图像的三维显示)
CR算法的优点是仅适用最近的4个点就可以确定一条平滑的曲线(G1连续),Catmull-Rom样条函数具有C1连续性质与快速插值能力,其每一个节点的导数值都是由其相邻的2个节点确定。他的原始公式是:
不过一般去t(tao)取1.
我的主要参考了Catmull-Rom splines Christopher Twigg March 11, 2003的文章,现在我没有在网上找到CR算法的原论文,如果谁找到了,希望您能传给我,谢谢了。
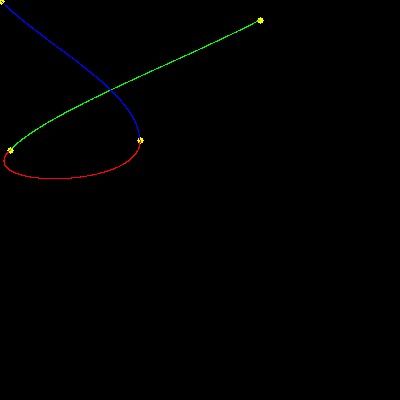
在参考上面提到的链接的程序上使用opencv作为工具终于可以画出平滑的曲线。
#include
#include
#include
#define COLOR_BLUE (cvScalar(255,0,0,0))
#define COLOR_GREEN (cvScalar(0,255,0,0))
#define COLOR_RED (cvScalar(0,0,255,0))
//void main()
//{
//
//}
void setColor(IplImage *img,CvPoint p ,CvScalar color)
{
char *ptr=(img->imageData+p.y*img->widthStep+p.x*3);
*(ptr+0) = color.val[0];
*(ptr+1) = color.val[1];
*(ptr+2) = color.val[2];
}
int main()
{
IplImage *img = cvCreateImage(cvSize(400,400),8,3);
cvZero(img);
CvPoint p0 = cvPoint(1,1);
CvPoint p1 = cvPoint(140,140);
CvPoint p2 = cvPoint(10,150);
CvPoint p3 = cvPoint(260,20);
cvCircle(img,p0,3,cvScalar(0,255,255,0),-1);
cvCircle(img,p1,3,cvScalar(0,255,255,0),-1);
cvCircle(img,p2,3,cvScalar(0,255,255,0),-1);
cvCircle(img,p3,3,cvScalar(0,255,255,0),-1);
/*CvPoint m0 = cvPoint((p1.x-p0.x)/2,(p1.y-p0.y)/2);
CvPoint m1 = cvPoint((p2.x-p0.x)/2,(p2.y-p0.y)/2);
CvPoint m2 = cvPoint((p3.x-p1.x)/2,(p3.y-p1.y)/2);
CvPoint m3 = cvPoint((p3.x-p2.x)/2,(p3.y-p2.y)/2);*/
CvPoint m0 = cvPoint((p1.x-p0.x),(p1.y-p0.y));
CvPoint m1 = cvPoint((p2.x-p0.x),(p2.y-p0.y));
CvPoint m2 = cvPoint((p3.x-p1.x),(p3.y-p1.y));
CvPoint m3 = cvPoint((p3.x-p2.x),(p3.y-p2.y));
double px;
double py;
for(double t = 0;t<1;t+=0.001)
{
double t_2 = t*t;
double _1_t = 1-t;
double _2t = 2*t;
double h00 = (1+_2t)*(_1_t)*(_1_t);
double h10 = t*(_1_t)*(_1_t);
double h01 = t_2*(3-_2t);
double h11 =t_2*(t-1);
px = h00 * p0.x + h10 * m0.x + h01 * p1.x + h11 * m1.x;
py = h00 * p0.y + h10 * m0.y + h01 * p1.y + h11 * m1.y;
setColor(img,cvPoint((int)px,(int)py),COLOR_BLUE);
px = h00 * p1.x + h10 * m1.x + h01 * p2.x + h11 * m2.x;
py = h00 * p1.y + h10 * m1.y + h01 * p2.y + h11 * m2.y;
//cvCircle(img,cvPoint((int)px,(int)py),1,cvScalar(0,0,255,0));
setColor(img,cvPoint((int)px,(int)py),COLOR_RED);
px = h00 * p2.x + h10 * m2.x + h01 * p3.x + h11 * m3.x;
py = h00 * p2.y + h10 * m2.y + h01 * p3.y + h11 * m3.y;
//cvCircle(img,cvPoint((int)px,(int)py),1,cvScalar(0,0,255,0));
setColor(img,cvPoint((int)px,(int)py),COLOR_GREEN);
}
cvShowImage("hello",img);
cvWaitKey();
return 0;
}
效果如下:
2.算法2:fant's resampleing 算法。
这个重新取样算法很简单,同样我也没有找到原论文,主要参考了“digital Image warping”和“ a simplified approch to image processing "这两本书。
这个算法的特点是简单、可以不完全复制输入序列,最大程度的保留了输入序列的离散程度。在第二本书的231-234页中给出了一个例子来具体说明这个算法,十分有助于理解这个算法。
算法的伪代码如下:
我的实现的代码如下:
#include
using namespace std;
void main()
{
double in[10] ={
2,4,10,20,60,
1,10,80,90,100
};
double out[10] ;
double inLen =10;
double outLen =5;
double scale=outLen/inLen;
double insfac = 1/scale;
double inSeg =1.0f;
double outSeg =insfac;
double acc=0;
int inIndex = 0;
int outIndex = 0;
double intensity;
while(outIndex 3.介绍完两个主要的插值算法后我来说说我对meshWarp算法的理解。
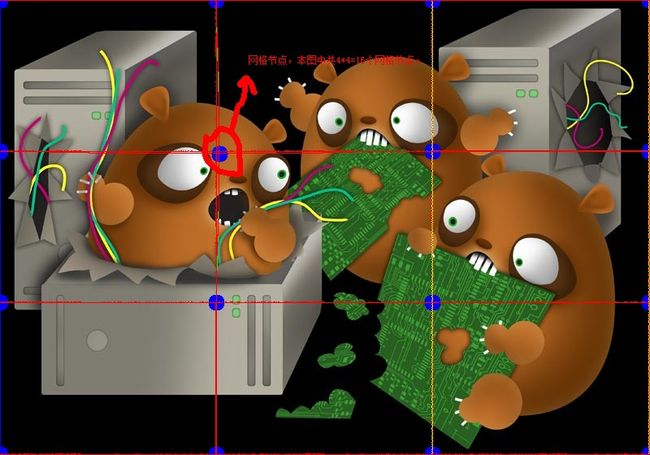
首先上张图:
1、 2次操作网格翘曲算法主要是通过对网格节点位置的移动来达到操作图像的目的,首先定义一个srcMesh在图中就是蓝色的小点,开辟存储空间把各个节点的位置记录下来。2、 通过鼠标移动某个或者某几个节点的位置,开辟存储空间记录下移动后的各个节点的位置,定义为dstMesh。3、定义图像的宽慰imgWidth、高为imgHeight。
第一次操作--------翘曲x坐标:
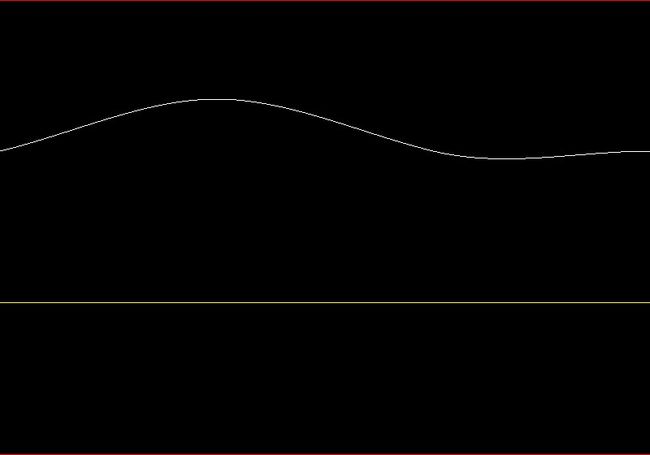
(1)使用catmull-rom算法把srcMesh的纵向的x插值,保存到已开辟内存的ts中。,
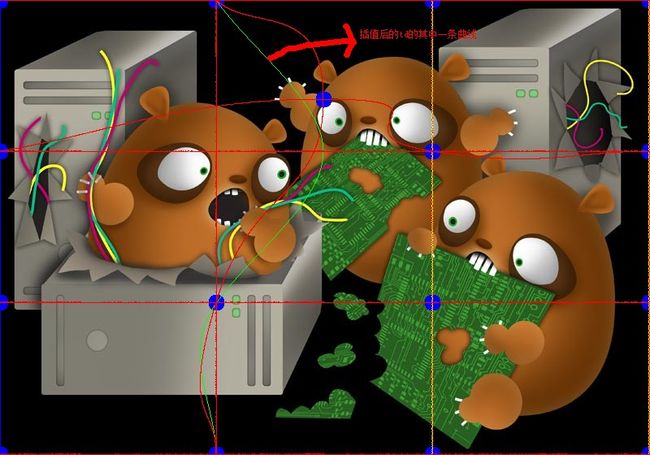
(2)使用catmull-rom算法把dstmesh的纵向的x坐标插值,保存到已开辟内存的td中。
td的第二条曲线在图中显示如下图绿色曲线所示:
(3)
{
for(int i=0;i操作1得到的图像如下图所示:可以看到只翘曲了x方向。

第二次操作--------翘曲y坐标:
方法基本上与上面的第一次操作相同,只不过把源图像换成了中间图像,把x坐标换成了y坐标。
通过catmull-rot算法插值得到的曲线如下图所示:
翘曲后的最终结果如下图所示:
总结:
算法的优点是简单,但是由上图的结果可以看出翘曲部分(小老鼠眼部),有类似于刮风的效果。给人的视觉效果不太好。
完。