混合密度模型Mixture Density Networks

翻译并简化自：http://blog.otoro.net/2015/11/24/mixture-density-networks-with-tensorflow/?tdsourcetag=s_pctim_aiomsg
notebook地址：
http://otoro.net/ml/ipynb/mixture/mixture.html
原文的TF代码+版本微调，和本人用Keras复现的，代码见 https://github.com/PancakeCard/mdn_keras

简单的数据拟合(用TF)

我们首先快速构建一个神经网络来拟合人造数据。我们看看一个只有一个隐藏层的神经网络是否能够拟合带有噪声的普通函数。
$$y=7.0\sin (0.75x)+0.5x+\epsilon$$

import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
import math
NSAMPLE = 1000
x_data = np.float32(np.random.uniform(-10.5, 10.5, (1, NSAMPLE))).T
r_data = np.float32(np.random.normal(size=(NSAMPLE,1)))
y_data = np.float32(np.sin(0.75*x_data)*7.0+x_data*0.5+r_data*1.0)

plt.figure(figsize=(8, 8))
plot_out = plt.plot(x_data,y_data,'ro',alpha=0.3)
plt.show()

我们定义一个简单的20个结点的单隐层神经网络
$$Y=W_{out}\tanh (WX+b)+b_{out}$$
(下述代码分别包括变量、隐藏层计算、损失函数、优化器、运行)

x = tf.placeholder(dtype=tf.float32, shape=[None,1])
y = tf.placeholder(dtype=tf.float32, shape=[None,1])

NHIDDEN = 20
W = tf.Variable(tf.random_normal([1,NHIDDEN], stddev=1.0, dtype=tf.float32))
b = tf.Variable(tf.random_normal([1,NHIDDEN], stddev=1.0, dtype=tf.float32))

W_out = tf.Variable(tf.random_normal([NHIDDEN,1], stddev=1.0, dtype=tf.float32))
b_out = tf.Variable(tf.random_normal([1,1], stddev=1.0, dtype=tf.float32))

hidden_layer = tf.nn.tanh(tf.matmul(x, W) + b)
y_out = tf.matmul(hidden_layer,W_out) + b_out

lossfunc = tf.nn.l2_loss(y_out-y);

train_op = tf.train.RMSPropOptimizer(learning_rate=0.1, decay=0.8).minimize(lossfunc)

sess = tf.InteractiveSession()
sess.run(tf.initialize_all_variables())

NEPOCH = 1000
for i in range(NEPOCH):
    sess.run(train_op,feed_dict={x: x_data, y: y_data})


x_test = np.float32(np.arange(-10.5,10.5,0.1))
x_test = x_test.reshape(x_test.size,1)
y_test = sess.run(y_out,feed_dict={x: x_test})

plt.figure(figsize=(8, 8))
plt.plot(x_data,y_data,'ro', x_test,y_test,'bo',alpha=0.3)
plt.show()
sess.close()

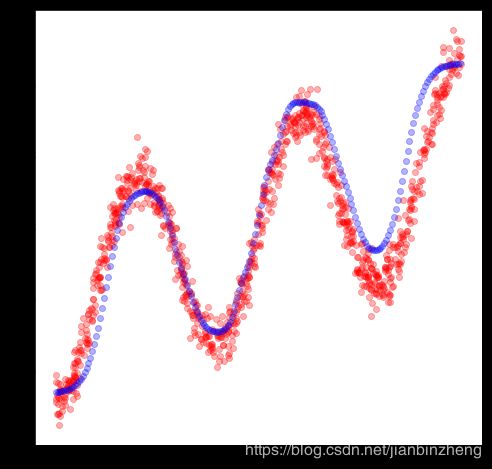
可以看到，神经网络可以很好的拟合这个正弦曲线函数。然而，这种类型的拟合方法只能对一对一，或多对一的函数有效，例如，我们将训练数据翻转
$$x=7.0\sin (0.75y)+0.5y+\epsilon$$

temp_data = x_data
x_data = y_data
y_data = temp_data

plt.figure(figsize=(8, 8))
plot_out = plt.plot(x_data,y_data,'ro',alpha=0.3)
plt.show()

如果我们用同样的方法来拟合这个翻转的数据，显然它效果很差，我们会看到神经网络被训练来拟合数据的平方平均数

sess = tf.InteractiveSession()
sess.run(tf.initialize_all_variables())

for i in range(NEPOCH):
  sess.run(train_op,feed_dict={x: x_data, y: y_data})

x_test = np.float32(np.arange(-10.5,10.5,0.1))
x_test = x_test.reshape(x_test.size,1)
y_test = sess.run(y_out,feed_dict={x: x_test})

plt.figure(figsize=(8, 8))
plt.plot(x_data,y_data,'ro', x_test,y_test,'bo',alpha=0.3)
plt.show()

sess.close()

我们当前的模型只能为每个输入值预测一个输出值，所以这种方法失败了。我们想要的是能够对每个输入有不同的输出值范围的模型。下一节，我们实现一个混合密度网络(Mixture Density Network, MDN)来实现这个任务。

混合密度网络

混合密度网络(MDNs)，由Christopher Bishop在90年代提出来解决这个问题。这个方法并不是让网络预测单一输出值，而是预测输出的整个概率分布。这个概念非常强大，且能够用于机器学习研究的许多领域。它能使我们能够计算一些预测中的置信因子。
我们用的反正弦数据并不只是个小问题，它在机器人领域有许多应用，例如，决策机器手臂应该朝哪个角度移动才能到达目标位置。MDNs也能用于对书写建模，如下一个线段从一个有多种可能性的概率分布中选择，而不是固定的一个结果。
Bishop的MDNs的实现预测了一个类别的概率分布，称作混合高斯分布(Mixture Gaussian distributions)，输出值被建模为多个高斯随机值的和，每个都有不同的均值和标准差。所以，对每个输入$x$，我们将预测一个概率分布函数(probability distribution function, pdf)$P(Y=y|X=x)$，即多个小的高斯概率分布的加权和
$$P(Y=y|X=x)=\sum _{k=0}^{K-1}{\Pi }_k(x)\varphi (y,{\mu }_k(x),{\sigma }_k(x)),\sum _{k=0}^{K-1}{\Pi }_k(x)=1$$
每个分布的参数${\Pi }_k(x),{\mu }_k(x),{\sigma }_k(x)$将由神经网络的输入$x$得到。且约束${\Pi }_k(x)$的和为1，以确保pdf加起来是100%。另外，${\sigma }_k(x)$必须是正的。
在我们的实现中，我们将用一个24个结点的隐藏层的神经网络，产生24个组分，因此对单个输入有72个输出值。我们定义分别为两部分
$$Z=W_o\tanh (W_{h}X+b_h)+b_o$$
$Z$是72维向量，可以分为三个部分，各24个，即
$${\Pi }_k=\frac{\exp (Z_k)}{{\sum }_{i=0}^{23}\exp (Z_i)},\sigma =\exp (Z_{24\to 43}),\mu =Z_{44\to 71}$$
${\Pi }_k$通过输入到softmax操作器中来确保和为1，且每个组分概率为正。
${\sigma }_k$通过指数操作确保为正
在Bishop的论文中，他注明了softmax和exp操作可以从贝叶斯框架的方法进行理论上的解释和可视化。

NHIDDEN = 24
STDEV = 0.5
KMIX = 24 # number of mixtures
NOUT = KMIX * 3 # pi, mu, stdev

x = tf.placeholder(dtype=tf.float32, shape=[None,1], name="x")
y = tf.placeholder(dtype=tf.float32, shape=[None,1], name="y")

Wh = tf.Variable(tf.random_normal([1,NHIDDEN], stddev=STDEV, dtype=tf.float32))
bh = tf.Variable(tf.random_normal([1,NHIDDEN], stddev=STDEV, dtype=tf.float32))

Wo = tf.Variable(tf.random_normal([NHIDDEN,NOUT], stddev=STDEV, dtype=tf.float32))
bo = tf.Variable(tf.random_normal([1,NOUT], stddev=STDEV, dtype=tf.float32))

hidden_layer = tf.nn.tanh(tf.matmul(x, Wh) + bh)
output = tf.matmul(hidden_layer,Wo) + bo

def get_mixture_coef(output):
    out_pi = tf.placeholder(dtype=tf.float32, shape=[None,KMIX], name="mixparam")
    out_sigma = tf.placeholder(dtype=tf.float32, shape=[None,KMIX], name="mixparam")
    out_mu = tf.placeholder(dtype=tf.float32, shape=[None,KMIX], name="mixparam")

    out_pi, out_sigma, out_mu = tf.split(output, 3, 1)

    max_pi = tf.reduce_max(out_pi, 1, keep_dims=True)
    out_pi = tf.subtract(out_pi, max_pi)

    out_pi = tf.exp(out_pi)

    normalize_pi = tf.reciprocal(tf.reduce_sum(out_pi, 1, keep_dims=True))
    out_pi = tf.multiply(normalize_pi, out_pi)

    out_sigma = tf.exp(out_sigma)

    return out_pi, out_sigma, out_mu

out_pi, out_sigma, out_mu = get_mixture_coef(output)
NSAMPLE = 2500

y_data = np.float32(np.random.uniform(-10.5, 10.5, (1, NSAMPLE))).T
r_data = np.float32(np.random.normal(size=(NSAMPLE,1))) # random noise
x_data = np.float32(np.sin(0.75*y_data)*7.0+y_data*0.5+r_data*1.0)

plt.figure(figsize=(8, 8))
plt.plot(x_data,y_data,'ro', alpha=0.3)
plt.show()

还是上一节的数据，我们不能简单地使用L2损失函数。一个更合适的损失函数时最小化分布和训练数据分布的对数似然函数
$$CostFunction(y|x)=-\log [\sum _k^K{\Pi }_k(x)\varphi (y,\mu (x),\sigma (x))]$$
所以训练集中每组(x,y)点，我们都能基于预测分布和真实点计算一个损失函数，并且尝试最小化它们的损失和。对于熟悉逻辑回归和交叉熵损失的人来说，这是类似的方法，但不是离散的。

oneDivSqrtTwoPI = 1 / math.sqrt(2*math.pi) # normalisation factor for gaussian, not needed.
def tf_normal(y, mu, sigma):
    result = tf.subtract(y, mu)
    result = tf.multiply(result,tf.reciprocal(sigma))
    result = -tf.square(result)/2
    return tf.multiply(tf.exp(result),tf.reciprocal(sigma))*oneDivSqrtTwoPI

def get_lossfunc(out_pi, out_sigma, out_mu, y):
    result = tf_normal(y, out_mu, out_sigma)
    result = tf.multiply(result, out_pi)
    result = tf.reduce_sum(result, 1, keep_dims=True)
    result = -tf.log(result)
    return tf.reduce_mean(result)

lossfunc = get_lossfunc(out_pi, out_sigma, out_mu, y)
train_op = tf.train.AdamOptimizer().minimize(lossfunc)

sess = tf.InteractiveSession()
sess.run(tf.initialize_all_variables())

NEPOCH = 10000
loss = np.zeros(NEPOCH) # store the training progress here.
for i in range(NEPOCH):
    sess.run(train_op,feed_dict={x: x_data, y: y_data})
    loss[i] = sess.run(lossfunc, feed_dict={x: x_data, y: y_data})

plt.figure(figsize=(8, 8))
plt.plot(np.arange(100, NEPOCH,1), loss[100:], 'r-')
plt.show()

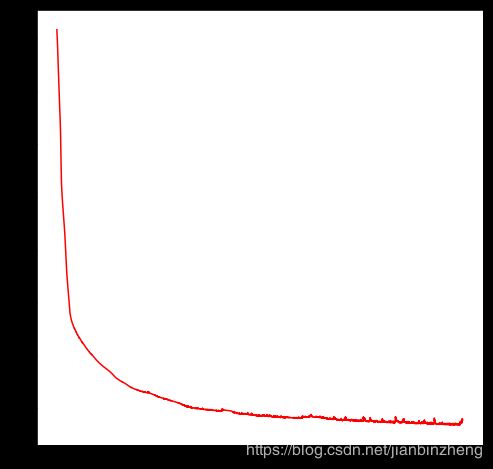
我们发现它大概在6000次迭代后停止进步。下一步我们要做的就是获取模型生成的分布，通过一些x坐标点，基于每个分布随机绘制绘制10个点，来产生对应的y轴坐标。这也可以看是否pdf生成的与训练数据匹配。
为了采样混合高斯分布，我们基于${\Pi }_k$集合随机选择一个分布，并基于$k^{th}$的高斯分布绘制点。

x_test = np.float32(np.arange(-15,15,0.1))
NTEST = x_test.size
x_test = x_test.reshape(NTEST,1) # needs to be a matrix, not a vector

def get_pi_idx(x, pdf):
    N = pdf.size
    accumulate = 0
    for i in range(0, N):
        accumulate += pdf[i]
        if (accumulate >= x):
            return i
    print ('error with sampling ensemble')
    return -1

def generate_ensemble(out_pi, out_mu, out_sigma, M = 10):
    NTEST = x_test.size
    result = np.random.rand(NTEST, M) # initially random [0, 1]
    rn = np.random.randn(NTEST, M) # normal random matrix (0.0, 1.0)
    mu = 0
    std = 0
    idx = 0

    # transforms result into random ensembles
    for j in range(0, M):
        for i in range(0, NTEST):
            idx = get_pi_idx(result[i, j], out_pi[i])
            mu = out_mu[i, idx]
            std = out_sigma[i, idx]
            result[i, j] = mu + rn[i, j]*std
    return result

out_pi_test, out_sigma_test, out_mu_test = sess.run(get_mixture_coef(output), feed_dict={x: x_test})

y_test = generate_ensemble(out_pi_test, out_mu_test, out_sigma_test)

plt.figure(figsize=(8, 8))
plt.plot(x_data,y_data,'ro', x_test,y_test,'bo',alpha=0.3)
plt.show()

如上图，我们把生成的数据点(蓝)绘制出来，且和训练数据(红)一同显示。我们的分布拟合了这些数据。我们也把这些数分布的均值$\mu (x)$打印出来，对每个点x坐标，有多条y可能的线或状态，我们根据${\Pi }_k$定义的概率选择

plt.figure(figsize=(8, 8))
plt.plot(x_test,out_mu_test,'go',alpha=0.5)
plt.plot(x_test,y_test,'bo',alpha=0.1)
plt.show()

最后，我们可以对每个x绘制出整个混合概率分布，得到热力图(不同组分概率相加)

x_heatmap_label = np.float32(np.arange(-15,15,0.1))
y_heatmap_label = np.float32(np.arange(-15,15,0.1))

def custom_gaussian(x, mu, std):
    x_norm = (x-mu)/std
    result = oneDivSqrtTwoPI*math.exp(-x_norm*x_norm/2)/std
    return result

def generate_heatmap(out_pi, out_mu, out_sigma, x_heatmap_label, y_heatmap_label):
    N = x_heatmap_label.size
    M = y_heatmap_label.size
    K = KMIX

    z = np.zeros((N, M)) # initially random [0, 1]

    mu = 0
    std = 0
    pi = 0

  # transforms result into random ensembles
    for k in range(0, K):
        for i in range(0, M):
            pi = out_pi[i, k]
            mu = out_mu[i, k]
            std = out_sigma[i, k]
            for j in range(0, N):
                z[N-j-1, i] += pi * custom_gaussian(y_heatmap_label[j], mu, std)
    return z

def draw_heatmap(xedges, yedges, heatmap):
    extent = [xedges[0], xedges[-1], yedges[0], yedges[-1]]
    plt.figure(figsize=(8, 8))
    plt.imshow(heatmap, extent=extent)
    plt.show()

z = generate_heatmap(out_pi_test, out_mu_test, out_sigma_test, x_heatmap_label, y_heatmap_label)
draw_heatmap(x_heatmap_label, y_heatmap_label, z)