大话数据结构十三：二叉树的链式存储结构（二叉链表）

1. 关于树

①树的度—也即是宽度，简单地说，就是结点的分支数。

②树的深度 — 组成该树各结点的最大层次。

③森林 — 指若干棵互不相交的树的集合。

④有序树 — 指树中同层结点从左到右有次序排列，它们之间的次序不能互换，这样的树称为有序树，否则称为无序树。

2. 二叉树的特点

i、每个结点最多有两颗子树

ii、左子树和右子树是有顺序的，次序不能任意颠倒

iii、即使树中某结点只有一颗子树，也要区分它是左子树还是右子树

3. 二叉树五种形态

① 空二叉树

②只有一个根结点

③根结点只有左子树

④ 根结点只有右子树

⑤ 根结点既有左子树又有右子树

4. 特殊的二叉树

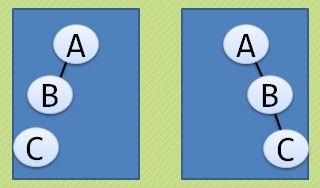
① 斜树：所有的结点都只有左子树的二叉树叫左斜树，所有的结点都只有右子树的二叉树叫右斜树，这两者统称为斜树。

② 满二叉树：在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子都在同一层上，这样的二叉树称为满二叉树。

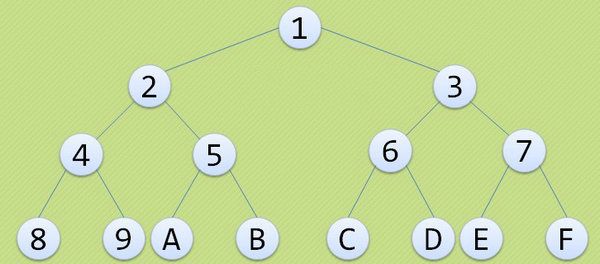
③ 完全二叉树：对一棵具有n个结点的二叉树按层序编号，如果编号为i (1<=i<=n) 的结点与同样深度的满二叉树中编号为i的结点位置完全相同，则这棵二叉树称为完全二叉树。

下图中不是完全二叉树，因为5没有左右子树，导致8，9，C，D，E，F 中间没有连续：

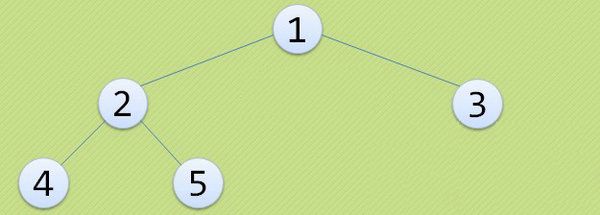
5. 二叉树的转换

将树转换为二叉树的步骤如下：

① 加线：所有兄弟节点之间加线

② 去线：保留树中每个结点与它第一个孩子的连线，删除其与其他孩子的连线

③ 层次调整：以根结点为轴心，将整棵树旋转，使之层次分明。

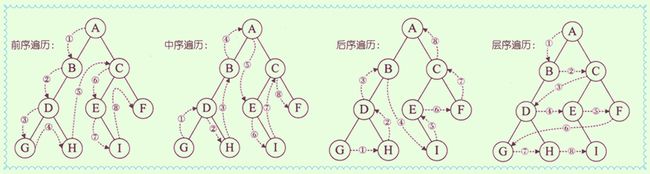
6. 二叉树的遍历(Java实现)

① 前序遍历：先访问根节点，再访问左子树，最后访问右子树。

② 中序遍历：先访问左子树，再访问根节点，最后访问右子树。

③ 后序遍历：先访问左子树，再访问右子树，最后访问根节点。

④ 层序遍历：从树的根结点开始，从上向下逐层访问，在同一层中，先左后右逐个访问。

public class LinkedBinaryTree {

	private Node root; // 根节点

	/**
	 * 内部节点类
	 */
	private class Node {
		private Node leftChild; // 左子节点
		private Node rightChild; // 右子节点
		private int data;

		public Node(int data) {
			this.leftChild = null;
			this.rightChild = null;
			this.data = data;
		}
	}

	public LinkedBinaryTree() {
		root = null;
	}

	/**
	 * 递归创建二叉树
	 * 
	 * @param node
	 * @param data
	 */
	public void buildTree(Node node, int data) {
		if (root == null) {
			root = new Node(data);
		} else {
			if (data < node.data) {
				if (node.leftChild == null) {
					node.leftChild = new Node(data);
				} else {
					buildTree(node.leftChild, data); // 递归遍历左子树
				}
			} else {
				if (node.rightChild == null) {
					node.rightChild = new Node(data);
				} else {
					buildTree(node.rightChild, data); // 递归遍历右子树
				}
			}
		}
	}

	/**
	 * 前序遍历（递归实现）
	 * 
	 * @param node
	 */
	public void preOrderTraverse(Node node) {
		if (node != null) {
			System.out.print(" " + node.data + " ");
			preOrderTraverse(node.leftChild);
			preOrderTraverse(node.rightChild);
		}
	}

	/**
	 * 中序遍历（递归实现）
	 * 
	 * @param node
	 */
	public void inOrderTraverse(Node node) {
		if (node != null) {
			inOrderTraverse(node.leftChild);
			System.out.print(" " + node.data + " ");
			inOrderTraverse(node.rightChild);
		}
	}

	/**
	 * 后序遍历（递归实现）
	 * 
	 * @param node
	 */
	public void postOrderTraverse(Node node) {
		if (node != null) {
			postOrderTraverse(node.leftChild);
			postOrderTraverse(node.rightChild);
			System.out.print(" " + node.data + " ");
		}
	}

	/**
	 * 前序遍历（非递归实现）
	 * 
	 * @param node
	 */
	public void preOrderTraverseNoRecursion(Node node) {
		Stack stack = new Stack();
		if (node != null) {
			stack.push(node); // 元素进栈
			while (!stack.isEmpty()) {
				node = stack.pop(); // 栈顶元素出栈
				System.out.print(" " + node.data + " ");
				if (node.rightChild != null)
					stack.push(node.rightChild);
				if (node.leftChild != null)
					stack.push(node.leftChild);
			}
		}
	}

	/**
	 * 中序遍历（非递归实现）
	 * 
	 * @param node
	 */
	public void inOrderTraverseNoRecursion(Node node) {
		Stack stack = new Stack();
		while ((node != null) || (!stack.isEmpty())) {
			if (node != null) {
				stack.push(node);
				node = node.leftChild;
			} else {
				node = stack.pop();
				System.out.print(" " + node.data + " ");
				node = node.rightChild;
			}
		}
	}

	/**
	 * 后序遍历（非递归实现）
	 * 
	 * @param node
	 */
	public void postOrderTraverseNoRecursion(Node node) {
		Stack stack = new Stack();
		Node preNode = null;
		if (node != null) {
			stack.push(node);
			while (!stack.isEmpty()) {
				node = stack.peek();
				if ((node.leftChild == null && node.rightChild == null) 
						|| (preNode != null && (preNode == node.leftChild || preNode == node.rightChild))) {
					System.out.print(" " + node.data + " ");
					stack.pop();
					preNode = node;
				} else {
					if (node.rightChild != null)
						stack.push(node.rightChild);
					if (node.leftChild != null)
						stack.push(node.leftChild);
				}
			}
		}
	}

	/**
	 * 层序遍历（非递归实现）
	 * 
	 * @param node
	 */
	public void levelOrderTraverse(Node node) {
		Queue queue = new LinkedList();
		if (node != null) {
			queue.offer(node); // 将元素插入队列
			while (!queue.isEmpty()) {
				node = queue.poll(); // 队列头部出列
				System.out.print(" " + node.data + " ");
				if (node.leftChild != null)
					queue.offer(node.leftChild);
				if (node.rightChild != null)
					queue.offer(node.rightChild);
			}
		}
	}

	/**
	 * 测试方法
	 * 
	 * @param args
	 */
	public static void main(String[] args) {
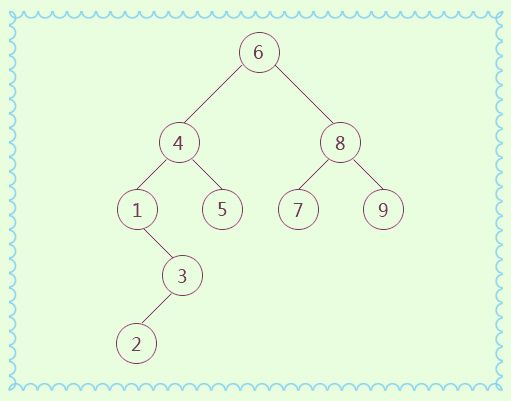
		int[] arr = { 6, 4, 8, 1, 7, 3, 9, 2, 5 };
		LinkedBinaryTree bTree = new LinkedBinaryTree();

		// 构建一棵二叉树
		for (int i = 0; i < arr.length; i++) {
			bTree.buildTree(bTree.root, arr[i]);
		}
		bTree.preOrderTraverse(bTree.root); // 前序遍历（递归）
		bTree.inOrderTraverse(bTree.root); // 中序遍历（递归）
		bTree.postOrderTraverse(bTree.root); // 后序遍历（递归）
		bTree.preOrderTraverseNoRecursion(bTree.root); // 前序遍历（非递归）
		bTree.inOrderTraverseNoRecursion(bTree.root); // 中序遍历（非递归）
		bTree.postOrderTraverseNoRecursion(bTree.root); // 后序遍历（非递归）
		bTree.levelOrderTraverse(bTree.root); // 层序遍历（非递归）
	}

}

递归创建的二叉树如下图：

打印结果：

①前序遍历（递归） ：6 4 1 3 2 5 8 7 9
② 中序遍历（递归） ：1 2 3 4 5 6 7 8 9
③ 后序遍历（递归） ：2 3 1 5 4 7 9 8 6
④前序遍历（非递归）：6 4 1 3 2 5 8 7 9
⑤ 中序遍历（非递归）：1 2 3 4 5 6 7 8 9
⑥ 后序遍历（非递归）：2 3 1 5 4 7 9 8 6
⑦ 层序遍历（非递归）：6 4 8 1 5 7 9 3 2