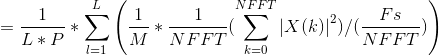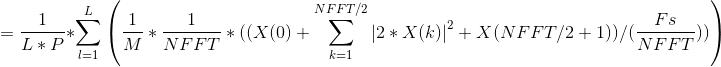谱估计,Welch法,不使用pwelch函数条件下实现。
帕塞瓦尔定理,离散序列情况下:
假设有以长度为N的离散随机序列![]() , 做NFFT点的傅里叶变换,得到
, 做NFFT点的傅里叶变换,得到![]() ,信号的采样频率为
,信号的采样频率为![]()
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
对于matlab使用fft函数的一点说明:
在采样频率为![]() 的条件下,
的条件下,
如果做FFT的点数(NFFT)为奇数的时候,FFT之后的频率范围为![]() ,对应的序列的长度为
,对应的序列的长度为![]() ;
;
如果做FFT的点数(NFFT)为偶数的时候,FFT之后的频率范围为![]() ,对应的序列的长度为
,对应的序列的长度为![]() ;
;
对于一段实数序列,做快速傅里叶变换之后既包含正频率,也包括负频率,由于负频率是没有实际意义的,绘制频谱图的时候要将这部分频率叠加到正频率上去,保证能量守恒。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
使用pwelch法要对数据进行分段
假设每段数据长度为M,数据总长度为N,重叠率overlap_rate, 那么数据可以分为L段,对于不足长度M的数据进行舍弃;
加窗函数条件下:
![]() 长度为M;
长度为M;
pwelch:
matlab程序:
clear;
close all;
clc;
% 程序说明:谱级估计
% 作者: JaingKe
% 日期: 2018/09/26
% 产生一段均值为0,方差为p的高斯白噪声序列
p = 2;
N = 204800; % 信号的数据长度
Fs = 1000; % 信号的采样频率
u = randn(N,1); % 产生长度为 N 的随机序列
a = sqrt(p);
noise = u * a;
power_u = var(noise); % 计算整段数据的方差
fprintf('整段高斯随机序列的方差: % .3f \n', power_u);
M = 2048; % 做fft 每一段数据的长度
nfft = 2048; % 做fft的点数
overlap_rate = 40; % 重叠率(百分比%)
Pfft = 10*log10(Fs/nfft);
n_overlap = ceil(M * overlap_rate * 0.01); % 重叠的点数,往大的方向取整
L = floor((N - n_overlap ) / (M - n_overlap)); % 计算分成了多少段数据
N_used = (M - n_overlap) * (L - 1) + M; % 实际使用的数据总长度
noise_used = noise(1:N_used,1);
window_fun = window(@rectwin, M);
P_win = sum(window_fun.^2)/M; % 窗函数能量的计算
if mod(nfft, 2) == 1 % 奇数
f = ((0 : (nfft + 1)/2) * Fs / nfft).';
fft_sum = zeros((nfft + 1)/2, 1);
abs_fft_half = zeros((nfft + 1)/2, 1);
else
f = ((0 : (nfft/2 )) * Fs / nfft).';
fft_sum = zeros((nfft/2 + 1), 1);
abs_fft_half = zeros((nfft/2 + 1), 1);
end
for n = 1:1:L
nstart = ( n - 1 )*(M - n_overlap);
temp_noise = noise_used(nstart + 1: nstart + M, 1).*window_fun;
temp_fft = fft(temp_noise)/nfft;
temp_fft_half = temp_fft(1: nfft/2 + 1, 1);
temp_fft_half(2:nfft/2,1) = 2*temp_fft_half(2:nfft/2,1);
abs_fft_half(1,1) = abs(temp_fft_half(1, 1)).^2;
abs_fft_half(nfft/2 + 1, 1) = abs(temp_fft_half(nfft/2 + 1,1)).^2;
abs_fft_half(2:nfft/2,1) = 0.5*abs(temp_fft_half(2:nfft/2, 1)).^2;
fft_sum = fft_sum(:,1) + 1 / P_win * abs_fft_half;
end
fft_sum = fft_sum ./ L;
figure(1);
plot(f, 10*log10(fft_sum)- Pfft,'-o');
title('自己计算和内置函数计算得到的结果对比');
xlabel('频率/Hz');
ylabel('谱级/dB');
grid on;
hold on;
pxx = pwelch(noise_used, window_fun, n_overlap, nfft, Fs);
plot(f, 10*log10(abs(pxx)));
legend('自己计算得到的','Pwelch函数得到的');
matlab仿真结果:可以看出两种方法计算得到的结果完全重合;
![\sum_{n=0}^{N-1}\left | x[n] \right |^{2}=\frac{1}{NFFT}\sum_{k=0}^{NFFT-1}\left | X(k) \right |^{2}](http://img.e-com-net.com/image/info8/ab61582db027435aa3f7bc6fa84d58c5.gif)
![\frac{1}{N}\sum_{n=0}^{N-1}\left | x[n] \right |^{2}=\frac{1}{N}*\frac{1}{NFFT}\sum_{k=0}^{NFFT-1}\left | X(k) \right |^{2}](http://img.e-com-net.com/image/info8/7d3ecc36a8da4875abf3f6399dea4dbb.gif)
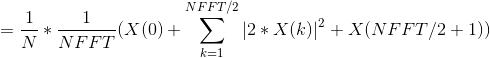
![\frac{1}{N}\sum_{n=0}^{N-1}\left | x[n] \right |^{2}/(\frac{Fs}{NFFT}) =\frac{1}{N}*\frac{1}{NFFT}(\sum_{k=0}^{NFFT-1}\left | X(k) \right |^{2})/(\frac{Fs}{NFFT})](http://img.e-com-net.com/image/info8/bc849674f13e4f71b354146553f81805.gif)

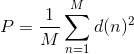
![\frac{1}{L*P}*\sum_{l=1}^{L}\left (\frac{1}{M}\sum_{n=(l-1)*(M-noverlap)}^{(l-1)*(M-noverlap)+M}\left | x[n] \right |^{2}/(\frac{Fs}{NFFT}) \right )](http://img.e-com-net.com/image/info8/64d3475f8a894ebeb7c9aa7c72e0cbc0.gif)