电机控制基础 --- (2)
作者:Stephen Du
免责声明: 本文为个人学习笔记及总结,仅代表个人观点,尽可能保证内容准确性。复制/转发请注明来源/作者。
欢迎添加微信交流学习。
接上一篇继续
文章目录
- 2. 电机参数
- 2.1 参数列表
- 2.2 参数关系
- 2.2.1 额定转速
- 2.2.2 功率和转矩
- 2.2.3 转矩与重力加速度
- 2.2.4 磁通量[^3]与电压
- 2.2.5 电压,电感,电流
- 2.2.6 转矩,体积,功率
- 2.3 参数测量
- 2.3.1 极对数测量
- 2.3.2 电阻测量
- 2.3.3 电感测量
- 2.3.4 反电动势常数测量
2. 电机参数
2.1 参数列表
电机厂商一般会在贴在电机上的铭牌或电机附带的说明书里面给出电机的基本参数。如:极对数,额定电压,额定电流,额定功率,额定转速,额定转矩等。如下图:
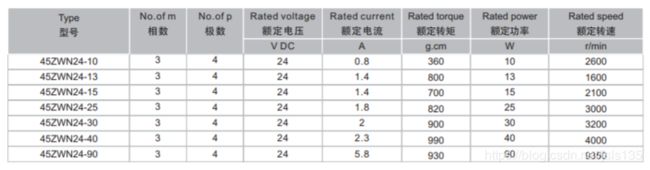
2.2 参数关系
2.2.1 额定转速
定义: 当反电动势达到最大值时电机仍产生最大转矩的转子速度。
反电动势等相关概念请见后面章节介绍。
2.2.2 功率和转矩
功率=电压*电流,这个公式是不是很熟悉,但参照上面的电机参数,你会发现这三者似乎没有一个满足这个关系式。这是为什么呢?额定电压和额定电流的乘积为总输入功率,但是受到各种因素影响,如电机转换效率,发热,摩擦等,输出功率一般都会小于输入功率,这些损耗的功率为无功功率。那电机的额定功率怎么计算,和哪些东西有关呢?
这里会引入另外一个物理量,转矩/扭矩(T)。其实这不难理解,功率和功有关,而功肯定需要力,而力和力矩之间又有联系。接下来我们看看他们到底是怎样的关系及推导过程。
功率 = 转矩 * 角速度: P = T ∗ ω P=T*\omega P=T∗ω
推导过程如下:
功率 = 功 / 时间: P = W t P=\frac{W}{t} P=tW
功 = 力 * 距离: W = F ∗ s W=F*s W=F∗s
速度 = 距离/时间 = 角速度 * 半径: v = s t = r ω v=\frac{s}{t}=r\omega v=ts=rω
扭矩 = 力 * 力臂(半径): T = F ∗ r T=F*r T=F∗r
由上述基本公式代入得到:
P = W t = F s t = F v = F r ω = T ω P=\frac{W}{t}=\frac{Fs}{t}=Fv=Fr\omega=T\omega P=tW=tFs=Fv=Frω=Tω
T = 9549 P 1 n 1 T=9549\frac{P_{1}}{n_{1}} T=9549n1P1
部分资料也有使用: T = 9550 P 1 n 1 T=9550\frac{P_{1}}{n_{1}} T=9550n1P1,这是因为除法的四舍五入。
上面公式看起来比较奇怪,尤其是9550这个常数,因为单纯线速度和角速度之间只有一个 2 π 2\pi 2π的关系,导致这个的原因是上面这个公式是在非国际单位下表示的。
下面是式子中各物理量的单位:
| 物理量 | 单位 | 物理量 | (国际)单位 |
|---|---|---|---|
| P1 | Kw | P | W |
| n1 | r/min(rpm) | n | r/s |
由于rpm及Kw在实际生活中使用更多,所以 T = 9549 P 1 n 1 T=9549\frac{P_{1}}{n_{1}} T=9549n1P1这个公式使用也更频繁。
推导过程如下:
角速度 = 2 π 2 \pi 2π * 转速: ω = 2 π n \omega = 2\pi n ω=2πn
由公式1得到: T = P ω T=\frac{P}{\omega} T=ωP
T = P ω = P 2 π n = 1000 P 1 2 π n 1 60 = 60 ∗ 1000 P 1 2 π n 1 ≈ 9549 P 1 n 1 T=\frac{P}{\omega}=\frac{P}{2 \pi n}=\frac{1000P_{1}}{2\pi \frac{n_{1}}{60}}=\frac{60*1000P_{1}}{2\pi n_{1}}\approx9549\frac{P_{1}}{n_{1}} T=ωP=2πnP=2π60n11000P1=2πn160∗1000P1≈9549n1P1
P = T n 1 / 9.549 P=Tn_{1}/9.549 P=Tn1/9.549
T = P ∗ 9.549 / n 1 = 10 ∗ 9.549 / 2600 ≈ 0.03673 T=P*9.549/n_{1}=10*9.549/2600\approx0.03673 T=P∗9.549/n1=10∗9.549/2600≈0.03673
怎么算出来不一样呢?这里需要注意我们公式中的T的单位为国际单位N·m(牛米),而表中的额定转矩360的单位是g.cm。g.cm又是个什么东西?
2.2.3 转矩与重力加速度
上面的g.cm里的g不是质量单位克,而是重力加速度。除了g.cm,我们还会看到如kg.m,g.m等。
严格来说应该为gfcm,克(g)是物体质量的单位,而这里应该为克力(gf)。但是大家都写为gcm。另外几个类似。
这个单位的来源是根据牛顿第二定律: F = m a = m g F=ma=mg F=ma=mg
| 物理量 | 单位 | 单位解释 |
|---|---|---|
| F(力) | N | 牛顿 |
| m(质量) | Kg | 千克 |
| g(重力加速度) | m/s2 | 米/秒2 |
如果我们取重力加速度g为9.8,可以得到: 1 k g m = 9.8 N m 1kgm=9.8Nm 1kgm=9.8Nm
1 g c m = 9.8 1000 ∗ 100 ( N m ) ≈ 0.0001 ( N m ) 1gcm = \frac{9.8}{1000*100} (Nm) \approx0.0001(Nm) 1gcm=1000∗1009.8(Nm)≈0.0001(Nm)
这里需要特别注意转矩/扭矩T的单位到底是什么,因为如果是gcm,那么结合前面的公式,功率和重力加速度可以有关系。重力加速度的常量9.8和前面公式的9.549非常接近,很容易弄混。但是两者的含义却完全不一样。
将上面这个转换关系带入上面的式子中是不是和表格给定的参数就非常接近了(不相等是因为计算过程中涉及除法运算,有舍入/舍出误差)。
2.2.4 磁通量1与电压
Φ = B ⋅ S ⋅ cos θ \Phi=\Beta\cdot S\cdot\cos\theta Φ=B⋅S⋅cosθ
由法拉第电磁感应定律得:
E = N Δ Ψ Δ t E = N\frac{\Delta\Psi}{\Delta t} E=NΔtΔΨ
E:感应电动势(V)。
N:感应线圈匝数。
Δ Ψ / Δ t \Delta\Psi/\Delta t ΔΨ/Δt:磁通量变化率(磁通对时间的导数)。
2.2.5 电压,电感,电流
E = L Δ i Δ t E = L\frac{\Delta i}{\Delta t} E=LΔtΔi
L = d Ψ d i L = \frac{d_\Psi}{d_i} L=didΨ
E:感应电动势(V)。
L:电感。
Ψ \Psi Ψ:磁通量。
2.2.6 转矩,体积,功率
电机的输出转矩和体积成正比,这比较好理解,相同的力(电流)体积越大,力臂越大,力矩就越大。
也就是说,再相同转速情况下,电机的体积和功率也成正比(见前文,功率和转矩成正比)。
转速高的电机一般功率密度要比速度低的电机要大。这也是为什么低速大转矩电机功率不大,但个头却很大,而转速很高的电机功率一般很大。
2.3 参数测量
很多控制策略需要依赖于电机的参数,但很多时候我们没有现成的参数,所以参数测量也是非常重要的一步,否则会影响其控制效果。常用的电机参数包含:极对数,电阻,电感,反电动势系数等。接下来分别介绍如果测量。
测量电机参数需要准备一些专业设备,如万用表,示波器,RLC表,电源等。
下面步骤中,RLC表使用前请校准。
2.3.1 极对数测量
这里提供两种方法,第一种不用电源,第二种需要电源。也有其他方法,但比较麻烦,需要的仪器设备也更多,这里就不描述了。
方法一:
-
示波器电压探头两路,同时连接电机任意两根线(不接电源)。
-
在电机转轴上做个标记,做标记的目的是要让你知道转了多少圈。
-
以标记位置开始,用手快速旋转电机一圈或者多圈(注意停下的位置不能超过标记位置了)。
-
观察示波器上的波形个数(一个周期算一个波形)或者数一下波峰个数。数出来的个数即为极对数。
方法二:
- 将电源电流限制到一个很小的值,可以先设置到额定电流的5%左右,电压设置比额定电压小,比如一半。
- 任意选择一根线(A相)接到电源正极,另外两根线(B、C相)相同时接到电源负极。
- 然后在电机上做标记(与法一一样),以这个标记位置开始旋转一圈,过程中你会感觉到有明显卡顿,记录卡顿的次数即为极对数(如果没有卡顿的感觉,可慢慢提高电压和电流的限制)。
2.3.2 电阻测量
- 万用表/RLC表选择电阻档,连接电机任意两根线(不接电源)。
- 记录值,重复第一步,用没有测试的一根线替换其中一根(3选2的组合)。
- 将3组数据求平均,然后除2就得到相电阻值(两根线是测得线电阻)。
2.3.3 电感测量
电感测量包含直轴电感(Ld)和交轴电感(Lq)(交直轴请见后文)。
Ld测量:
- 任意选择一根线(A相)接到电源正极,另外两根线(B、C相)相同时接到电源负极。
- 和前面测量极对数的方法二一样,供一个小的电压电流使其对齐,保持电机别动。示波器电压探头接到B/C相上面,电流探头接到A相上面。
- 再将正负极的线反过来接(A相接负极,BC同时接正极),记录波形(如下图)。然后通过公式计算:
L d = 2 3 τ R L_d =\frac{2}{3}\tau R Ld=32τR
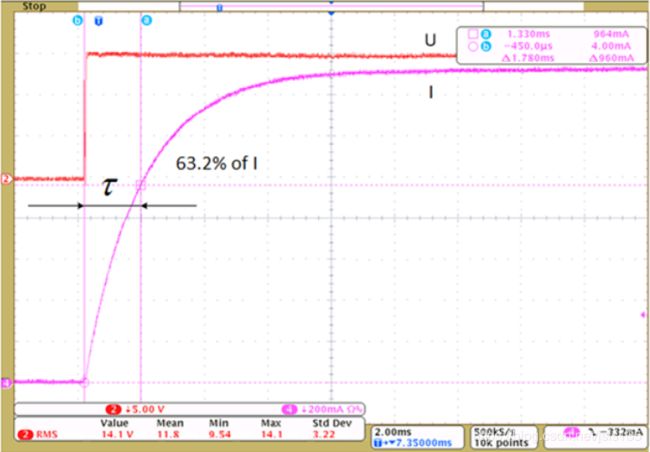
Lq测量(方法和Ld类似):
- B相接电源正极,C相接电源负极,A相悬空不接。
- 供一个小的电压电流使其对齐,保持电机不动,示波器电压探头接到A相上面,电流探头接到B/C相上面。
- 再将A相接电源正极,BC同时接电源负极,记录波形,使用前面Ld一样的公式计算Lq。
2.3.4 反电动势常数测量
- 示波器电压探头两路,同时连接电机任意两根线(不接电源)。
- 在电机转轴上做个标记,做标记的目的是要让你知道转了多少圈。
- 以标记位置开始,用手快速旋转电机一圈。
- 示波器记录所产生波形的周期及峰峰值,然后使用后面公式进行计算: K e = V p k − p k ⋅ T e 4 3 π ⋅ 1000 K_e=\frac{V_{pk-pk}\cdot T_e}{4\sqrt{3}\pi\cdot1000} Ke=43π⋅1000Vpk−pk⋅Te。其中Vpk-pk是峰峰值,Te是周期。
磁通量表示磁场分布情况的物理量。通过磁场中某处的面元dS的磁通量dΦ定义为该处磁感应强度的大小B与dS在垂直于B方向的投影dScosθ的乘积,即dFB =BdScosθ式中θ是面元的法线方向n与磁感应强度B的夹角。磁通量是标量,θ<90°为正值,θ>90°为负值。通过任意闭合曲面的磁通量 ΦB 等于通过构成它的那些面元的磁通量的代数和,即对于闭合曲面,通常取它的外法线矢量(指向外部空间)为正。磁场的高斯定理指出,通过任意闭合曲面的磁通量为零,即它表明磁场是无源的,不存在发出或会聚磁力线的源头或尾闾,亦即不存在孤立的磁单极。以上公式中的B既可以是电流产生的磁场,也可以是变化电场产生的磁场,或两者之和。 ↩︎