LeetCode5. Longest Palindromic Substring(马拉车算法 Manacher Algorithm)

一、问题描述

Given a string s, find the longest palindromic substring *（最长回文字符串）*in s. You may assume that the maximum length of s is 1000.

Example:

Input: “babad”

Output: “bab”

Note: “aba” is also a valid answer.

Example:

Input: “cbbd”

Output: “bb”

---

二、思路（关键点）

1. 查找字符串中的最长回文字符串；

2. Trick（字符串预处理）

   （本节引用自https://www.felix021.com/blog/read.php?2040）

   用一个非常巧妙的方式：将所有可能的奇数/偶数长度的回文子串都转换成了奇数长度：在每个字符的两边都插入一个特殊的符号。

   比如 abba 变成 #a#b#b#a#， aba变成 #a#b#a#。
   为了进一步减少编码的复杂度，可以在字符串的开始加入另一个特殊字符，这样就不用特殊处理越界问题，比如$#a#b#a#
   （注意，下面的代码是用C语言写就，由于C语言规范还要求字符串末尾有一个’\0’所以正好OK，但其他语言可能会导致越界）。

   例子：
   （1）以字符串12212321为例，
   经过上一步，变成了 S[] = “$#1#2#2#1#2#3#2#1#”;
   这样，以#为中心的回文串，在原串中就是偶回文串。以字符为中心的回文串，在原串中是奇回文串。

   （2）然后用一个数组 P[i] 来记录以字符S[i]为中心的最长回文子串向左/右扩张的长度（包括S[i]，也就是把该回文串“对折”以后的长度），比如S和P的对应关系：
   S # 1 # 2 # 2 # 1 # 2 # 3 # 2 # 1 #
   P 1 2 1 2 5 2 1 4 1 2 1 6 1 2 1 2 1
   (p.s. 可以看出，P[i]-1正好是原字符串中回文串的总长度）

3. 马拉车算法 Manacher Algorithm（代码分析）

   本节引用自作者：233 Magic，讲解的很清晰，感谢作者分享
   链接：https://www.zhihu.com/question/37289584/answer/71483487

   我们再规定两个数组与几个变量的意义:
   （1）数组Ma[i]：代表添加了“#”后的字符串。
   （2）数组Mp[i]：代表以字符串第i位为中心的回文串的最大长度。
   （3）变量Mx：代表当前“已经匹配完毕的结尾最远的回文串”到达了Ma[]数组的第Mx位。
   （4）变量ID：代表当前“已经匹配完毕的结尾最远的回文串”中心为Ma[]数组的第ID为。
   在此借用一下 知乎@邝斌 菊苣的模板中的C++代码来进行算法说明。
   

   逐行来看。16行就不必说啦！
   第17行，循环变量i代表了当前正在判断Ma串的第i位为中心的回文子串最长长度。
   第18行，是整个算法最核心的部分，也是O(n)时间复杂度的保障。
   我们考虑到，假如当前的i已经被包含在曾经被判断过的回文串内（即Mx>i)，那么它在这个回文串中相对应的那个字符Ma[2*ID-i]，（即处于i位置的字符，相对于ID中心对称的[2*ID-i]位置），应当已经被计算过以它为中心的回文串可以有多长了。那么，我们以第i位为中心的回文串长度，就有了第一个下限Mp[2*ID-i]。
   但是，我们考虑到，以Ma[2*ID-i]为中心的回文串，它可能延展到了以Ma[ID]为中心的回文串之外。这样我们就不能保证以Ma[i]为中心的回文串包括了以Ma[ID]为中心的回文串之外的部分。所以我门得到了第二个下限Mx-i。

   第19行，考虑到第18行我们只得到了一个可怜的下限（……我们要在这个下限的基础上继续向外扩展。（画外音：教练，这个暴力匹配怎么保证复杂度还是O(n)呢！Σ( ° △ °|||)︴）
   对于这一步的算法复杂度分析，我们可以分为三种情况考虑当前这一位i，在第18行的位置所执行的操作：
   ①Mp[i]=1，说明Mx没有覆盖超过i，那么Mx的値在这一步执行后一定会增加。
   ③Mp[i]=Mp[ID*2-i]，说明可怜的Ma[i]只有这么长已经匹配不出去了。。T_T
   考虑到，Mx的値是单调的，并且始终不会超过字符串长度Len，那么对于所有的i，①、②种情况的执行时间总和不会超过Len。因此总时间复杂度依旧是O(n)。

   第20行，更新Mx和ID的値。。

4. 马拉车算法 Manacher Algorithm（图解）
   另外，上面提到的博客也给出了下述图解说明，个人感觉也比较清晰，感谢作者分享。转载过来更方便理解。
   （本节引用自https://www.felix021.com/blog/read.php?2040）

   当然光看代码还是不够清晰，还是借助图来理解比较容易。

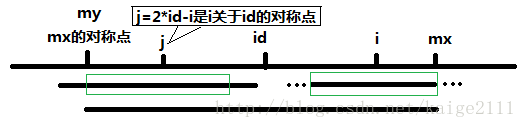
   （1）当 mx - i > P[j] 的时候，以S[j]为中心的回文子串包含在以S[id]为中心的回文子串中，由于 i 和 j 对称，以S[i]为中心的回文子串必然包含在以S[id]为中心的回文子串中，所以必有 P[i] = P[j]，见下图。
   

   （2）当 P[j] >= mx - i 的时候，以S[j]为中心的回文子串不一定完全包含于以S[id]为中心的回文子串中，但是基于对称性可知，下图中两个绿框所包围的部分是相同的，也就是说以S[i]为中心的回文子串，其向右至少会扩张到mx的位置，也就是说 P[i] >= mx - i。至于mx之后的部分是否对称，就只能老老实实去匹配了。
   

   （3）对于 mx <= i 的情况，无法对 P[i]做更多的假设，只能P[i] = 1，然后再去匹配了。

5. 计算回文串的长度
   回文串起始位置：(maxIdx - maxSpan) / 2
   回文串长度：(maxIdx + maxSpan - 1) / 2 - 1 - (maxIdx - maxSpan) / 2 +1 =(2*maxSpan-1) / 2

---

三、程序示例

C#版本

class Program
{
     public static string preProcess(string s)
     {
         StringBuilder sb = new StringBuilder();
         sb.Append("$");
         for (int i = 0; i < s.Length; i++)
         {
             sb.Append("#");
             sb.Append(s[i]);
         }

         sb.Append("#");
         //sb.Append("$");

         return sb.ToString();
     }

     public static string LongestPalindrome(string s)
     {
         if (s==null || s.Length==0)
         {
             return null;
         }

         string str = preProcess(s);
         //当前能够向右延伸的最远的回文串中心点，随迭代而更新
         int idx = 0;

         //当前最长回文串在总字符串所能延伸到的最右端的位置
         int max = 0;

         //当前已知的最长回文串中心点
         int maxIdx = 0;

         //当前已知的最长回文串向左或向右能延伸的长度
         int maxSpan = 0;

         int[] p = new int[str.Length];

         for (int curr = 1; curr < str.Length; curr++)
         {
             //找出当前下标相对于idx的对称点
             int symmetryofCur = 2 * idx - curr;
             // 如果当前已知延伸的最右端大于当前下标，我们可以用对称点的P值，否则记为1等待检查
             p[curr] = (max > curr) ? Math.Min(p[symmetryofCur], max - curr) : 1;
             // 检查并更新当前下标为中心的回文串最远延伸的长度
             while ((curr + p[curr])// 检查并更新当前已知能够延伸最远的回文串信息
             if ((curr + p[curr]) > max)
             {
                 max = p[curr] + curr;
                 idx = curr;
             }

             // 检查并更新当前已知的最长回文串信息
             if (p[curr]>maxSpan)
             {
                 maxSpan = p[curr];
                 maxIdx = curr;
             }
         }

         return s.Substring((maxIdx - maxSpan) / 2, (maxIdx + maxSpan - 1) / 2 - 1 - (maxIdx - maxSpan) / 2 +1 );
     }


     static void Main(string[] args)
     {
         string str = "abaaba";
         //string str = "eabcb";
         string result = LongestPalindrome(str);
     }
 }

END.