ID3算法

1. ID3

1.1  ID3算法原理

ID3是一种基于决策树的分类算法，由J.Ross Quinlan在1986年开发。id3根据信息增益，运用自顶向下的贪心策略建立决策树。信息增益用于度量某个属性对样本集合分类的好坏程度。由于采用了信息增益，id3算法建立的决策树规模比较小，查询速度快。id3算法的改进是C4.5算法，C4.5算法可以处理连续数据，采用信息增益率，而不是信息增益。理解信息增益，需要先看一下信息熵。

熵：

在信息增益中，衡量标准是看特征能够为分类系统带来多少信息，带来的信息越多，该特征越重要。对一个特征而言，系统有它和没它时信息量将发生变化，而前后信息量的差值就是这个特征给系统带来的信息量。所谓信息量，就是熵。

假如有变量X，其可能的取值有n种，每一种取到的概率为 ，那么X的熵就定义为

 是概率密度函数；对数是以2为底；

对于分类系统来说，类别C是变量，每一种取到的概率为，n为类别总数，此时分类系统的熵就是。

信息增益是针对一个一个的特征而言的，就是看一个特征t，系统有它和没它的时候信息量各是多少，两者的差值就是这个特征给系统带来的信息量，即增益。系统含有特征t的时候信息量很好计算，就是刚才的式子，它表示的是包含所有特征时系统的信息量。

对应到系统中，就是下面的等价：（1）系统不包含特征t；（2）系统虽然包含特征t，但是t已经固定了，不能变化。一个特征X，它可能的取值有n多种（x1，x2，……，xn），当计算条件熵而需要把它固定的时候，要把它固定在哪一个值上呢？答案是每一种可能都要固定一下，计算n个值，然后取均值才是条件熵。而取均值也不是简单的加一加然后除以n，而是要用每个值出现的概率来算平均（简单理解，就是一个值出现的可能性比较大，固定在它上面时算出来的信息量占的比重就要多一些）。

因此有这样两个条件熵的表达式：

特征X被固定为值时的条件熵 

特征X被固定时的条件熵 ，两者关系是

具体到我们文本分类系统中的特征t，t有几个可能的值呢？注意t是指一个固定的特征，比如他就是指关键词“经济”或者“体育”，当我们说特征“经济”可能的取值时，实际上只有两个，“经济”要么出现，要么不出现。一般的，t的取值只有t（代表t出现）和（代表t不出现），注意系统包含t但t 不出现与系统根本不包含t可是两回事。

因此固定t时系统的条件熵就有了，为了区别t出现时的符号与特征t本身的符号，我们用T代表特征，而用t代表T出现，那么：

比照前面的式子，就是T出现的概率，就是T不出现的概率。展开，其中

另一半为

因此特征T给系统带来的信息增益就是系统原理的熵减去固定特征T后的条件熵之差：

表示类别出现的概率，即1除以类别总数(这是在平等看待每个类别而忽略它们的大小的时候这样算，如果考虑了大小，需要把大小的影响加进去)。表示特征t出现的概率，即出现过t的文档数除以总文档数即可。表示出现t的时候，类别出现的概率，即出现了t并且属于类别的文档数除以出现了t的总文档数。

1.2 ID3算法流程

输入：样本集合S，属性集合A
输出：id3决策树。
1) 若所有种类的属性都处理完毕，返回；否则执行2）
2）计算出信息增益最大属性a，把该属性作为一个节点。
     如果仅凭属性a就可以对样本分类，则返回；否则执行3）
3）对属性a的每个可能的取值v，执行一下操作：
      i.  将所有属性a的值是v的样本作为S的一个子集Sv；
      ii. 生成属性集合AT=A-{a};
      iii.以样本集合Sv和属性集合AT为输入，递归执行id3算法；

1.3 举例说明

1.3.1 这个例子来源于Quinlan的论文。
     假设，有种户外活动。该活动能否正常进行与各种天气因素有关。不同的天气因素组合会产生两种后果，也就是分成2类：能进行活动或不能。我们用P表示该活动可以进行，N表示该活动无法进行。下表描述样本集合是不同天气因素对该活动的影响。

Day	Outlook	Temperature	Humidity	Wind	Play ball
D1	Sunny	Hot	High	Weak	No
D2	Sunny	Hot	High	Strong	No
D3	Overcast	Hot	High	Weak	Yes
D4	Rain	Mild	High	Weak	Yes
D5	Rain	Cool	Normal	Weak	Yes
D6	Rain	Cool	Normal	Strong	No
D7	Overcast	Cool	Normal	Strong	Yes
D8	Sunny	Mild	High	Weak	No
D9	Sunny	Cool	Normal	Weak	Yes
D10	Rain	Mild	Normal	Weak	Yes
D11	Sunny	Mild	Normal	Strong	Yes
D12	Overcast	Mild	High	Strong	Yes
D13	Overcast	Hot	Normal	Weak	Yes
D14	Rain	Mild	High	Strong	No

 

属性值outlook, temperature, humidity, 和wind，各自的值是

outlook = { sunny, overcast, rain }

temperature = {hot, mild, cool }

humidity = { high, normal }

wind = {weak, strong }

1.3.2 

该活动无法进行的概率是：5/14
该活动可以进行的概率是：9/14
因此样本集合的信息熵是：-5/14log(5/14) - 9/14log(9/14) = 0.940

1.3.3 

接下来我们再看属性outlook信息熵的计算：
outlook为sunny时，该活动无法进行的概率是：3/5，可以进行的概率是：2/5
因此sunny的信息熵是：-3/5log(3/5) - 2/5log(2/5) = 0.971
同理可以计算outlook属性取其他值时候的信息熵：
outlook为overcast时的信息熵：0
outlook为rain时的信息熵：0.971
属性outlook的信息增益：gain(outlook) = 0.940 - (5/14*0.971 + 4/14*0 + 5/14*0.971) = 0.246

相似的方法可以计算其他属性的信息增益：
gain(temperature) = 0.029 
gain(humidity) = 0.151
gain(windy) = 0.048
信息增益最大的属性是outlook

1.3.4 

根据outlook把样本分成3个子集，然后把这3个子集和余下的属性作为输入递归执行算法。

Ssunny = {D1, D2, D8, D9, D11} = 5 

gain(Ssunny, humidity) = 0.970

gain(Ssunny, temperature) = 0.570

gain(Ssunny, wind) = 0.019

信息增益最大的属性是humidity

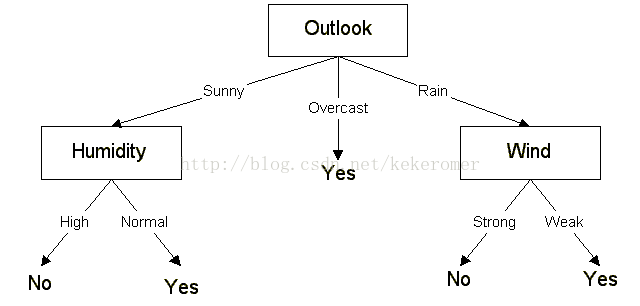
 结果

The final decision = tree

The decision tree can also be expressed in rule format:

IF outlook = sunny AND humidity = high THEN playball = no

IF outlook = rain AND humidity = high THEN playball = no

IF outlook = rain AND wind = strong THEN playball = no

IF outlook = overcast THEN playball = yes

IF outlook = rain AND wind = weak THEN playball = yes