零基础入门数据挖掘Task1&2
Datawhale 零基础入门数据挖掘-Task1&2
快速浏览
- Datawhale 零基础入门数据挖掘-Task1&2
- Task1 赛题理解
- 赛题目的
- 评价指标
- Task2 数据分析
- EDA简介
- 探索性数据分析
- Reference
Task1 赛题理解
这次是以阿里天池的一个入门比赛“零基础入门数据挖掘 - 二手车交易价格预测”为例学习,希望它能“火”成一个经典数据挖掘入门题供大家学习。
赛题以二手车市场为背景,要求选手预测二手汽车的交易价格,这是一个典型的回归问题。通过这道赛题来引导大家走进AI数据竞赛的世界,主要针对于于竞赛新人进行自我练习、自我提高。
赛题目的
浏览完赛题具体数据及其它官方信息后了然,赛题已知15万条二手汽车的交易价格信息(每条二手车信息包含31项变量信息),欲解决测试集对应二手汽车的交易价格预测。
评价指标
评价标准为MAE(Mean Absolute Error),即平均绝对值误差,它表示预测值和观测值之间绝对误差的平均值。这是一种常见的评价指标。
M A E = ∑ i = 1 n ∣ y i − y ^ i ∣ n MAE = \frac{\sum_{i=1}^n \left|y_i - \hat{y} _{i} \right|}{n} MAE=n∑i=1n∣yi−y^i∣
事实上,MAE越小,说明模型预测得越准确。在训练模型时可以借助sklearn中已有的MAE评测来检验自己模型对测试集拟合的效果,源代码在此。也可以对应此题自己编写一个简易的MAE评价指标。
# coding=utf-8
import numpy as np
#定义自己编写的MAE评价指标
def test_mae(y_true, y_pred):
mae_value = np.mean(np.abs(y_pred - y_true))
return mae_value
#下面分别测试自己编写的MAE评价指标和sklearn的MAE评价指标
y_true = np.array([1.0, 5.0, 4.0, 3.0, 2.0, 5.0, -3.0])
y_pred = np.array([1.0, 4.5, 3.8, 3.2, 3.0, 4.8, -2.2])
print('test_MAE:',test_mae(y_true, y_pred))
#调用sklearn中的MAE
from sklearn import metrics
print('sklearn_MAE:',metrics.mean_absolute_error(y_true, y_pred))
#test_MAE: 0.4142857142857143
#sklearn_MAE: 0.4142857142857143
Task2 数据分析
EDA简介
探索性数据分析(Exploratory Data Analysis,简称EDA),对已有数据在尽量少的先验假设下通过作图、制表、方程拟合、计算特征量等手段探索数据的结构和规律。
简而言之,就是要了解数据集,以便于后续开发模型。“兵马未动,粮草先行”,EDA的重要性也是“粮草”级别的。
探索性数据分析
题目给出的测试集有15万条二手汽车信息,验证集有5万条。一条二手车信息中包含31项变量信息,其中15项匿名变量,其余16项变量(含价格变量)。实际上划分变量就是30项自变量(包含数字型变量、类别型变量、文本型变量和时间型变量),1项因变量(整数形式的二手车交易价格)。
SaleID(交易ID)是唯一编码,不作为后续有效变量的考虑。seller(销售方)在测试集中只有一条是“非个体”,其余十四万九千九百九十九都是“个体”。offerType(报价类型)在测试集中只有一种。因此也选择放弃这两项变量。
| 有效变量名 | 描述 | 类型 |
|---|---|---|
| v系列特征 | 匿名特征,包含v0-14在内15个匿名特征 | 数字 |
| power | 发动机功率:范围 [ 0, 600 ] | 数字 |
| kilometer | 汽车已行驶公里,单位万km | 数字 |
| regDate | 汽车注册日期,例如20160101,2016年01月01日 | 时间 |
| creatDate | 汽车上线时间,即开始售卖时间 | 时间 |
| name | 汽车交易名称,已脱敏 | 类别 |
| model | 车型编码,已脱敏 | 类别 |
| brand | 汽车品牌,已脱敏 | 类别 |
| bodyType | 车身类型:豪华轿车:0,微型车:1,厢型车:2,大巴车:3,敞篷车:4,双门汽车:5,商务车:6,搅拌车:7 | 类别 |
| fuelType | 燃油类型:汽油:0,柴油:1,液化石油气:2,天然气:3,混合动力:4,其他:5,电动:6 | 类别 |
| gearbox | 变速箱:手动:0,自动:1 | 类别 |
| notRepairedDamage | 汽车有尚未修复的损坏:是:0,否:1 | 类别 |
| regionCode | 地区编码,已脱敏 | 类别 |
#类别变量值的分布情况
categorical_features=[ 'name', 'model', 'brand', 'bodyType', 'fuelType','gearbox','notRepairedDamage', 'regionCode']
for i in categorical_features:
print(i+'有%i个不同的特征值'%train[i].nunique())
print(train[i].value_counts())
#notRepairedDamage存在除“是:0,否:1”外的情况
train['notRepairedDamage'].value_counts()
#0.0 111361
#- 24324
#1.0 14315
#Name: notRepairedDamage, dtype: int64
事实上对每一个变量进行数据查看缺省情况的时候可以发现,在“汽车有尚未修复的损坏”上的“ - ”也是一种空缺的表现,先将其替换成NAN。然后查看整体缺省情况发现,凡有缺省的信息都被删除,则原15万条交易信息只剩118326条有效交易信息
#处理'notRepairedDamage'
train['notRepairedDamage'].replace('-', np.nan, inplace=True)
train['notRepairedDamage'].value_counts()
#0.0 111361
#1.0 14315
#Name: notRepairedDamage, dtype: int64
#train缺省情况
train.isnull().sum()
'''
SaleID 0
name 0
regDate 0
model 1
brand 0
bodyType 4506
fuelType 8680
gearbox 5981
power 0
kilometer 0
notRepairedDamage 24324
regionCode 0
seller 0
offerType 0
creatDate 0
price 0
v_0 0
v_1 0
v_2 0
v_3 0
v_4 0
v_5 0
v_6 0
v_7 0
v_8 0
v_9 0
v_10 0
v_11 0
v_12 0
v_13 0
v_14 0
dtype: int64
'''
#凡有缺省的信息都被删除,则原15万条交易信息只剩118326条有效交易信息
train.dropna().describe()
此外,无论是测试集还是验证集中power(发动机功率)都超过600的存在,这也是后续需要处理的地方。其中,测试集有143条power(发动机功率)超过600的信息,验证集有70条。
train['power'].describe()
'''
count 150000.000000
mean 119.316547
std 177.168419
min 0.000000
25% 75.000000
50% 110.000000
75% 150.000000
max 19312.000000
Name: power, dtype: float64
'''
test['power'].describe()
'''
count 50000.000000
mean 119.883620
std 185.097387
min 0.000000
25% 75.000000
50% 109.000000
75% 150.000000
max 20000.000000
Name: power, dtype: float64
'''
train['power'][train['power']>600].count()
#143
train['power'][train['power']>600].count()
#70
时间类型就是汽车注册时间和开始售卖时间,这两个就留在特征处理中解决。
最后对我们的预测目标price(二手车交易价格)进行分析。分析训练集中price的情况发现,价格不服从正态分布,对数变换处理后结果接近正态分布,但无界约翰逊分布拟合效果更佳。
import scipy.stats as st
y = train['price']
plt.figure(1); plt.title('Normal')
sns.distplot(y, kde=False, fit=st.norm)
plt.figure(2); plt.title('Log Normal')
sns.distplot(y, kde=False, fit=st.lognorm)
plt.figure(3); plt.title('Johnson SU')
sns.distplot(y, kde=False, fit=st.johnsonsu)
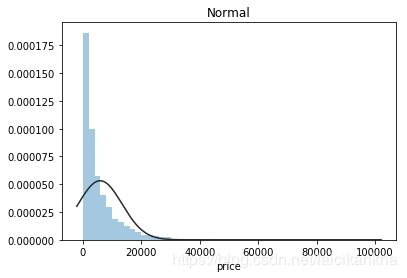
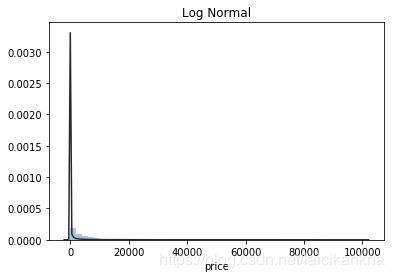
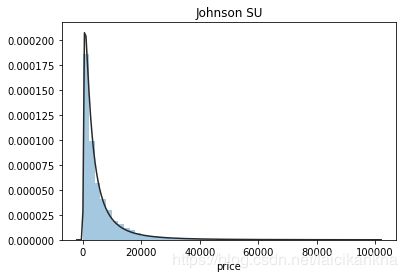
不过时间匆匆,无界约翰逊分布也没有找到,接下来用比较常用的对数变换来做价格的转换。
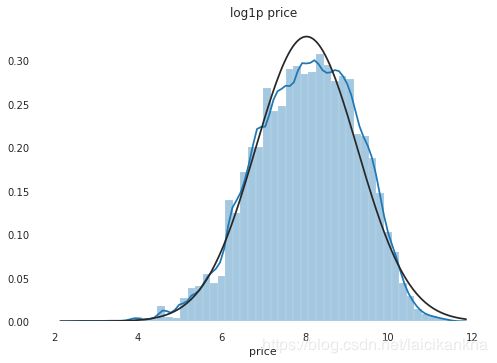
# 目标值做log(x+1)处理
train_price = np.log1p(train['price'])
plt.figure(); plt.title('log1p price')
sns.distplot(train_price, fit=st.norm)
numeric_features = ['power', 'kilometer', 'v_0', 'v_1', 'v_2', 'v_3', 'v_4', 'v_5', 'v_6', 'v_7', 'v_8', 'v_9', 'v_10', 'v_11', 'v_12', 'v_13','v_14' ]
#数字型变量和价格的相关性
numeric_features.append('price')
price_numeric = train[numeric_features]
correlation = price_numeric.corr()
print(correlation['price'].sort_values(ascending = False),'\n')
'''
price 1.000000
v_12 0.692823
v_8 0.685798
v_0 0.628397
power 0.219834
v_5 0.164317
v_2 0.085322
v_6 0.068970
v_1 0.060914
v_14 0.035911
v_13 -0.013993
v_7 -0.053024
v_4 -0.147085
v_9 -0.206205
v_10 -0.246175
v_11 -0.275320
kilometer -0.440519
v_3 -0.730946
Name: price, dtype: float64
'''
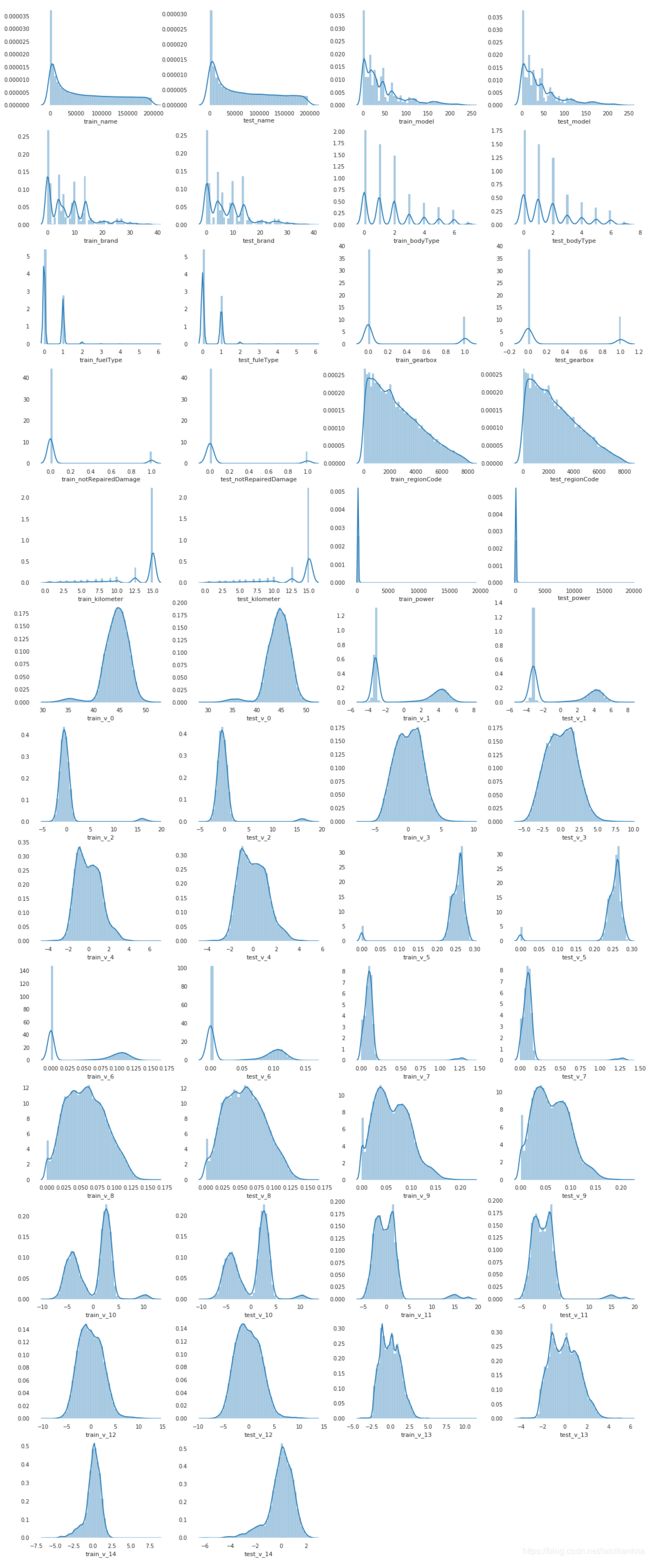
最后直观感受一下测试集和验证集之间的变量值分布情况,大体上是差不多的,后续做特征工程也要根据于此。
Reference
- Datawhale 零基础入门数据挖掘-Task1 赛题理解
- Datawhale 零基础入门数据挖掘-Task2 数据分析
- sklaern分类评价指标
- EDA简单分析报告