概率,悖论,以及理性人原则(python实现)
- 用Python实现对概率P的定义
- 热身问题掷骰子
- 增强版P接受对事件的断言
- 两儿童悖论
- 问题1年长者是男孩两儿童都是男孩的概率
- 问题2至少一个是男孩两个都是男孩的概率
- 理性人原则
- 问题3 一个男孩生在周二两个都是男孩的概率
- 可视化
- 睡美人悖论
- 蒙提霍尔悖论11
- 非等概率输出概率分布
- 问题4一个男孩生在2月29两个都是男孩的概率
- 仿真
- 未完待续
在这篇手札里,我们将涉及概率论的基本原理,以及它们的python实现。(你首先应具备概率论和Python的基础知识.)最后我们将演示如何解决几个复杂但又有趣的有关概率论的悖论。
200多年以前, Pierre-Simon Laplace 写下:
一个事件的概率是支持该事件的情况的数目与所有可能情况数目的比值,前提[这些事件]等可能发生。… 因此简单地说,概率是一个分子是支持该事件的情况数目,分母为所有可能的情况的数目的一个分数。
回到当时的水平,拉普拉斯其实揭露了概率的本质。如果你想解开一个概率问题(无论是否是悖论),你所需要做的无非是给出情况的精确定义,以及认真地计算支持该事件的情况的个数和全部所有可能的情况的数目。我们将以对这些术语的定义开始这篇文章:
- 试验(Experiment):通过观测能够得到的一种输出不确定的事件
例如:掷筛子。 - 输出(outcome):实验的结果,空间中的一种特定状态。“情况”(“case”)的同义词。
例如:6。 - 样本空间(sample space):对某一试验而言,所有可能的输出值所组成的集合。(本文假设所有输出等概率发生)。
例如,{1, 2, 3, 4, 5, 6} - 事件(event):我们所感兴趣的具有某种性质的可能输出值组成的样本空间的子集。
例如,“掷出的筛子是偶数”这一事件是输出值{2, 4, 5}组成的集合。 - 概率(Probability):样本空间的大小除以事件所有可能输出值的个数。
例如,掷一个六面筛子,掷出的是偶数值的概率是|{2, 4, 6}|/|{1, 2, 3, 4, 5, 6}| = 3/6 = 1/21
用Python实现对概率P的定义
from fractions import Fraction
from __future__ import division
def P(event, space):
"在一个等可能发生的样本空间中,事件发生的概率"
return Fraction(len(event & space), len(space))将这段代码2和因此简单地说,概率是一个分子是支持该事件的情况数目,分母为所有可能的情况的数目的一个分数。这句话做对照。注意这里我用Fraction而不是一般的除法是因为我想要得到一个像 1/3 一样的精确值,而不是 0.3333333333333333 .
热身问题:掷骰子
我们来考虑抛掷一个均匀的六面的筛子的试验,记样本空间为 D :
D = {1, 2, 3, 4, 5, 6}事件得到的是一个偶数值的概率可以通过如下的方式计
算:
even = {2, 4, 6}
P(even, D)输出为:
Fraction(1, 2)这种计算方法很不优雅,我必须显式地枚举所有从1到6的偶数值。如果我希望处理一个特殊的筛子,比如一个12或者20面的筛子,我必须回到even的定义式并重新定义even。我更倾向于一次性定义even以及所有(返回True和False)的断言函数,只要P能接受那样的参数。
增强版P,接受对事件的断言
如果我们能够将一个事件指定为输出值的集合或者对全部可能输出值的断言,将会很赞。让我们来实现它:
def P(event, space):
"""在一个等可能发生的样本空间中,事件发生的概率 . 事件可以是输出值的集合,或者是一个断言(属于事件的输出值为真)"""
if callable(event):
event = such_that(event, space)
return Fraction(len(event & space), len(space))
def such_that(predicate, collection):
"集合中满足断言为真的元素构成的子集"
return {e for e in collection if predicate(e)}def even(n): return n%2 == 0
such_that(even, D)输出为:
{2, 4, 6}P(even, D)输出为:
Fraction(1, 2)D12 = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
such_that(even, D12)输出为:
{2, 4, 6, 8, 10, 12}P(even, D12)输出为:
Fraction(1, 2)(注:such_that的功能如同python内置的filter3,只不过**such_that返回的是一个set而不是list)
两儿童悖论
1959年,Martin Gardner 提出了如下的两个问题:
问题1. 琼斯先生有两个孩子。年长的是男孩。请问两个都是男孩的概率?
问题2. 斯密斯先生有两个孩子。至少有一个是男孩。请问两个都是男孩的概率?
2010年,Gary Foshee增加了这样的一个问题:
- 问题3. 我又两个小孩。至少一个生在周二。请问两个小孩都是男孩的概率?
问题2和问题3被认为是悖论,因为人们对之有着令人惊奇的答案。
(注:假设所有的输出都是等概率,不考虑51%的新生儿是男孩,诸如此类的问题)
问题1:年长者是男孩。两儿童都是男孩的概率?
我们使用BG来标记年长者是男孩,年小者是女孩。则采样空间S:
S = {'BG', 'BB', 'GB', 'GG'}我们分别来定义两个都是男孩和年长者是男孩条件下的断言函数,
def two_boys(outcome): return outcome.count('B') == 2
def older_is_a_boy(outcome): return outcome.startswith('B')现在我们可以回答问题14了:
P(two_boys, such_that(older_is_a_boy, S))结果为:
Fraction(1, 2)问题2:至少一个是男孩。两个都是男孩的概率?
很容易仿真这一问题并找到最终的答案:
def at_least_one_boy(outcome): return 'B' in outcomeP(two_boys, such_that(at_least_one_boy, S))输出为:
Fraction(1, 3)然而,真正理解这一问题是很困难的。一些人认为问题的答案应当是 1/2 。我们能够验证我们的答案 1/3 吗?我们能够看到当条件是至少一个是男孩有三个等概率的输出5:
such_that(at_least_one_boy, S)输出为:
{'BB', 'BG', 'GB'}在这三个输出中,只有一种情况下两个都是男孩,因此 1/3 的答案得到了验证。
但一些人仍然认为问题的答案应当是 1/2 ,他们的理由是如果一个是男孩,有两种等概率的可能性对另一个小孩而言,因此另一个小孩是男孩的概率,也就是两个都是男孩的概率是1/2.
当两种思路得出了两种不同的答案,便产生了一个悖论。下面是对这一悖论的三种回复:
- 数学的基石本身即是不完备的。这个问题正好揭示了这一点
- 我们的才是对的,所有与我的答案不同的都是错的
- 我有对问题的一种解释下的正确答案,而你的是另一种解释下的正确答案。
如果你是Bertrand Russell6或者Georg Cantor,也许能够揭开数学基本原理上存在的缺陷。平凡如你我,我更推荐第三种对这一悖论的回复。当我相信答案是 1/3 ,而我如果听到有的人的答案是 1/2 ,我的回应会是实在是有趣!一定存在着对这一问题不同的解释;我应该试着去揭示他们的解释是什么,以及为什么它们的答案也是对的。
首先我明确描述我对这一试验的理解:
- 试验2a:随机地从拥有两个孩子的家庭中选择出斯密斯先生家。他被问及是否他的一个孩子是男孩,他的回答是是的。
然后我设想出对该试验的另一种可能的解释:
- 试验2b:随机地从拥有两个孩子的家庭中选择出斯密斯先生家。随机地从他照看孩子的时机中选择一次进行观测。观测的结果是这个孩子是男孩。
试验2b需要一个新的样本空间来表示,我们称之为S2b,它包含8个输出,而不是之前的四个;对之前的样本空间S而言,我们有两种观测的可能性要么是年长的(*?),要么是年幼的(?*)。接下来我们会使用记号GB/g?来标识年长的是女孩,年幼的是男孩,年长的被观测出是一个女孩,年幼的未被观测。新的样本空间是:
S2b = {'BB/b?', 'BB/?b',
'BG/b?', 'BG/?g',
'GB/g?', 'GB/?b',
'GG/g?', 'GG/?g'}现在我们能够得到样本空间中的观察到斯密斯先生和他的儿子这一子集:
def observed_boy(outcome): return 'b' in outcome
such_that(observed_boy, S2b)输出为:
{'BB/?b', 'BB/b?', 'BG/b?', 'GB/?b'}最终我们可以确定斯密斯先生有两个儿子的概率,在其中一个是男孩的条件之上:
P(two_boys, such_that(observed_boy, S2b))输出为:
Fraction(1, 2)这一悖论得到解释。两个理性之人对同一问题得出不同的解释,而且每一种解释都毫无漏洞的得到最终的结论, 1/3 或者 1/2 。哪一种解释更好?我们可以继续辩论,或者我们就此达成一致,使用不具有歧义性质的问题描述(也就是使用试验2a和试验2b的描述语言,而不是问题2的描述语言)。
理性人原则
告诉你一个很不幸的事实是,我们人类经常做出的假设是凡与我不通知人皆笨蛋。如 George Carlin所言你有没有留意过当你开车的时候所有开得比你慢的人你骂它们笨蛋,所有开得比你快的人你骂它们疯子?
他者更可能是理性的而不是笨蛋的这一假设,被称作理性人原则。它是卡内基梅隆大学计算机学院的指导原则,也是我试图养成的思维准则。
现在让我们回到更具悖论性质的问题。
问题3. 一个男孩生在周二。两个都是男孩的概率?
一个孩子生在周二,另外一个也生在周二的概率;
此时所谓的1/2(两者之间不构成影响)也将受到破坏;
显然仍然是条件概率,在一个孩子生在周二的条件下,问两个都生在周二的概率。
解题思路仍然是构造空间,一个7行7列的表格,每一行表示第一个孩子的出生在一周的第几天,每一列表示第二个孩子出生在一周的第几天,第二行和第二列表示至少有一个孩子生在周二,共14-1=13种可能数,在这种条件之下,另一个孩子也生在周二(也即两个孩子均生在周二)的可能数为1,也即行列的交汇处,故概率为1/13。
2016/01/13 补充
当Gary Foshee第一次提出这个问题,绝大多数人都无法想象婴儿的生日和性别之间的关系,然后感觉答案与问题2相同。但是为了精确地描述问题,我们应首先陈述试验是什么,以及样本空间的定义,然后计算,等等。
- 试验3a:随机地从拥有两个孩子的家庭中选择一个家庭。当她被问及是否她的一个儿子生在周二时。她的回答是是的。
接下来我们定义样本空间。我们将使用记号G1B3来标记年长的是一个生在一周的第一天(周日)的女孩,年幼的是一个生在一周的第三天(周二)的男孩。我们称新的样本空间为S3。
sexesdays = {sex+day for sex in 'BG' for day in '1234567'}
S3 = {older+younger for older in sexesdays for younger in sexesdays}断言7
assert len(S3) == (2*7)**2
print(sorted(S3))输出为:
['B1B1', 'B1B2', 'B1B3', 'B1B4', 'B1B5', 'B1B6', 'B1B7', 'B1G1', 'B1G2', 'B1G3', 'B1G4', 'B1G5', 'B1G6', 'B1G7', 'B2B1', 'B2B2', 'B2B3', 'B2B4', 'B2B5', 'B2B6', 'B2B7', 'B2G1', 'B2G2', 'B2G3', 'B2G4', 'B2G5', 'B2G6', 'B2G7', 'B3B1', 'B3B2', 'B3B3', 'B3B4', 'B3B5', 'B3B6', 'B3B7', 'B3G1', 'B3G2', 'B3G3', 'B3G4', 'B3G5', 'B3G6', 'B3G7', 'B4B1', 'B4B2', 'B4B3', 'B4B4', 'B4B5', 'B4B6', 'B4B7', 'B4G1', 'B4G2', 'B4G3', 'B4G4', 'B4G5', 'B4G6', 'B4G7', 'B5B1', 'B5B2', 'B5B3', 'B5B4', 'B5B5', 'B5B6', 'B5B7', 'B5G1', 'B5G2', 'B5G3', 'B5G4', 'B5G5', 'B5G6', 'B5G7', 'B6B1', 'B6B2', 'B6B3', 'B6B4', 'B6B5', 'B6B6', 'B6B7', 'B6G1', 'B6G2', 'B6G3', 'B6G4', 'B6G5', 'B6G6', 'B6G7', 'B7B1', 'B7B2', 'B7B3', 'B7B4', 'B7B5', 'B7B6', 'B7B7', 'B7G1', 'B7G2', 'B7G3', 'B7G4', 'B7G5', 'B7G6', 'B7G7', 'G1B1', 'G1B2', 'G1B3', 'G1B4', 'G1B5', 'G1B6', 'G1B7', 'G1G1', 'G1G2', 'G1G3', 'G1G4', 'G1G5', 'G1G6', 'G1G7', 'G2B1', 'G2B2', 'G2B3', 'G2B4', 'G2B5', 'G2B6', 'G2B7', 'G2G1', 'G2G2', 'G2G3', 'G2G4', 'G2G5', 'G2G6', 'G2G7', 'G3B1', 'G3B2', 'G3B3', 'G3B4', 'G3B5', 'G3B6', 'G3B7', 'G3G1', 'G3G2', 'G3G3', 'G3G4', 'G3G5', 'G3G6', 'G3G7', 'G4B1', 'G4B2', 'G4B3', 'G4B4', 'G4B5', 'G4B6', 'G4B7', 'G4G1', 'G4G2', 'G4G3', 'G4G4', 'G4G5', 'G4G6', 'G4G7', 'G5B1', 'G5B2', 'G5B3', 'G5B4', 'G5B5', 'G5B6', 'G5B7', 'G5G1', 'G5G2', 'G5G3', 'G5G4', 'G5G5', 'G5G6', 'G5G7', 'G6B1', 'G6B2', 'G6B3', 'G6B4', 'G6B5', 'G6B6', 'G6B7', 'G6G1', 'G6G2', 'G6G3', 'G6G4', 'G6G5', 'G6G6', 'G6G7', 'G7B1', 'G7B2', 'G7B3', 'G7B4', 'G7B5', 'G7B6', 'G7B7', 'G7G1', 'G7G2', 'G7G3', 'G7G4', 'G7G5', 'G7G6', 'G7G7']下面的两条语句表明至少一个男孩的概率都是 3/4 ,无论是在样本空间S3还是S。
P(at_least_one_boy, S3)输出为:
Fraction(3, 4)P(at_least_one_boy, S)输出为:
Fraction(3, 4)同理,两样本空间中都是男孩的概率是:
P(two_boys, S3)输出为:
Fraction(1, 4)P(two_boys, S)输出为:
Fraction(1, 4)同理,两样本空间中:至少一个是男孩条件下的两个都是男孩的概率:
P(two_boys, such_that(at_least_one_boy, S3b))输出为:
Fraction(1, 3)P(two_boys, such_that(at_least_one_boy, S))输出为:
Fraction(1, 3)我们接下来定义至少一个男孩生在周二(一周的第三天)这一断言:
def at_least_one_boy_tues(outcome): return 'B3' in outcome现在我们能够回答问题38了:
P(two_boys, such_that(at_least_one_boy_tues, S3))输出为:
Fraction(13, 27)1327 与预想的 13 差的很远(但是更接近与 12 )。因此至少有一个男孩生在周二不同于至少有一个男孩。你对此感到意外吗?你能接受这个答案,或者我们在哪里计算出了错?还有其他对这一实验的解释,能够导致同样的结果的吗?
这里有一个可替代的解释:
- 实验3b:随机地从拥有两个孩子的家庭中选择一对父母。随机地从她照看孩子的时机中选择一次。孩子被观测到是一个男孩,且声称它的生日在周二。
在这一样本空间中我们可以将输出表示为G1B3/??b3类似这样的记号,这一记号标识着年长的孩子是一个女该她生在周日,年幼的男孩生在周二,年长的没有被观测到,年幼的被观测到了。
def observed_boy_tues(outcome): return 'b3' in outcome
S3b = {older + younger + '/' + observation
for older in sexesdays
for younger in sexesdays
for observation in [older.lower()+'??', '??'+younger.lower()]}现在我们可以回答问题3了:
P(two_boys, such_that(observed_boy_tues, S3b))结果为:
Fraction(1, 2)因此,对于问题使用试验3b的描述得出的结果和试验2b相同。
还是很让人困惑?让我们使用可视化工具9让问题变得更加实际而具体。
可视化
我们将以二维输出表的形式展示结果,其中的每一个单元格是通过颜色编码的输出,不满足任何我们需要的断言的输出(单元格)为白色;如果输出包含两个男孩则为绿色;满足断言,但不包含两个男孩为黄色。每一行的单元格中具有相同年长者,每一列的单元格具有相同的年幼者。如下是实现代码:
from IPython.display import HTML
def table(space, n=1, event=two_boys, condition=older_is_a_boy):
"""Display sample space in a table, color-coded: green if event and condition is true;
yellow if only condition is true; white otherwise."""
# n is the number of characters that make up the older child.
olders = sorted(set(outcome[:n] for outcome in space))
return HTML('' +
cat(row(older, space, event, condition) for older in olders) +
'
' +
str(P(event, such_that(condition, space))))
def row(older, space, event, condition):
"Display a row where an older child is paired with each of the possible younger children."
thisrow = sorted(outcome for outcome in space if outcome.startswith(older))
return '' + cat(cell(outcome, event, condition) for outcome in thisrow) + ' '
def cell(outcome, event, condition):
"Display outcome in appropriate color."
color = ('lightgreen' if event(outcome) and condition(outcome) else
'yellow' if condition(outcome) else
'ghostwhite')
return '{} '.format(color, outcome)
cat = ''.join我们可以使用这一可视化工具重新看待问题1,如图,有一个输出包含两个男孩(绿色单元格)在年长者是男孩(绿色或者黄色)的情况之中,因此在给定年长者是男孩条件下的两个都是男孩的概率是 1/2 。
table(S, 1, two_boys, older_is_a_boy)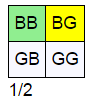
对于问题2,如图,我们可以看出在给定条件至少一个是男孩(绿色和黄色)下,两个都是男孩的概率是 1/3 。
table(S, 1, two_boys, at_least_one_boy)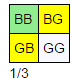
结果仍然是 1/3 当我们考虑出生日的时候。(我们让每一个单元格变得更大通过枚举一周七天)
table(S3, 2, two_boys, at_least_one_boy)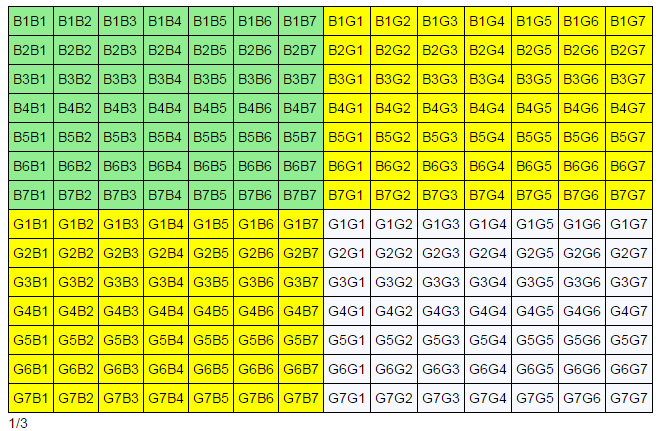
现在考虑问题三的悖论性:
table(S3, 2, two_boys, at_least_one_boy)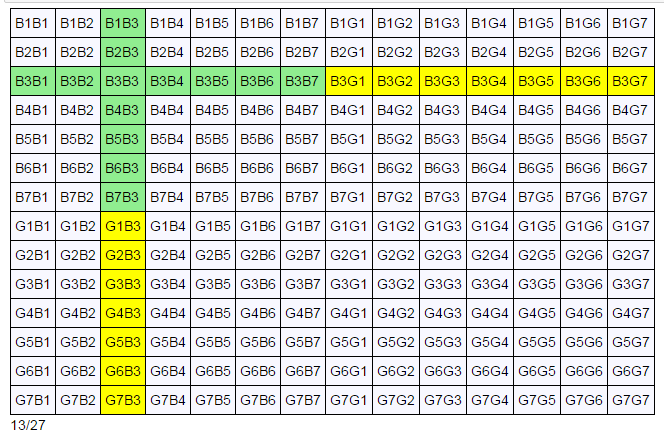
从图中我们可以看到,有27个相关的输出,其中13个是绿色的。这无疑增加了 13/27 是正确的感觉。这幅图像也提供给我们一种思考为什么答案不是1/3的方法。将黄+绿色的区域视为具有一个重叠单元格一个水平条和一个垂直条。每一个条状区域都是一半黄一半绿,因此如果不存在重叠区域,绿色的概率将是1/2。当条状区域(变宽)占据着一半的样本空间时,此时的重叠区域达到最大,概率是1/3。在问题3对应的表格里,重叠区域很小,因此最终的概率值更接近于1/2(略小于) 10。
一种看待这一问题的方式是如果我告诉你一些特定的信息(例如一个男孩生在周二),比较不太可能同时作用在两个孩子上,因此我们有较小的重叠区域,也即概率值接近1/2.但如果我告诉你的是一些相对宽泛的信息(比如是一个男孩),这同时作用在两个孩子上的可能性就相对较大,这便会导致更大的重叠区域,更小的概率值,接近1/3。
睡美人悖论
睡美人问题是另一个具有迷惑性的问题。
睡美人自愿接受如下的一个试验,并被告知如下的试验细节:在周末要求她进入睡眠状态。偶尔地,在试验期间,睡美人将会被唤醒,接受采访,并接受诱发失忆的药物进入睡眠。一个均匀的硬币会被抛掷来确定试验流程。如果硬币正面朝上,睡美人只会在周一唤醒并接受采访。如果硬币反面朝上,她会在周一和周二唤醒且接受采访。无论哪种情况,她都会在周三被唤醒,不经历采访实验结束。在睡美人唤醒的时间里,接受采访,被问及的问题都是“在你的观念里硬币朝上的概率是多少?”
当睡美人接访问时,她应该如何回答?首先,她需要确定样本空间。她可以使用形如‘heads/monday/interviewed’的记号标识输出值(硬币)正面朝上,这是周一,接受访问。因此应该有四种等可能的输出:
B = {'heads/monday/interviewed', 'heads/monday/sleep',
'tails/monday/interviewed', 'tails/tuesday/interviewed'}这时,你可能期望我做出如下的断言:
def heads(outcome): return 'heads' in outcome
def interviewed(outcome): return 'interviewed' in outcome对此我们已经司空见惯了,我认为是时候遵循“不要重复自己”的原则了,因此我会定义一个定义断言函数的函数:
def T(property):
return lambda outcome: property in outcome现在我们可以得到答案:
heads = T('heads')
interviewed = T('interviewed')
P(heads, such_that(interviewed, B))输出为:
Fraction(1, 3)蒙提霍尔悖论11
这是最为著名的概率悖论之一。该问题是这样被介绍的:
假设你现在参加一个游戏竞赛节目,你有三个门可以选择:其中一扇门后是一辆车,另外两扇门后是山羊,你选中了其中一扇门,记做No.1。主持人,他知道门后有什么,打开了另一扇门,记做No.3,门后是一只山羊。然后他问你,“你是否想换成No.2门?”此时转换选择是明智的选择吗?
关于此问题,已有很多文章的做了充分的介绍,但为了求解该问题我们需要做的仅仅是小心地理解这一问题,以及对样本空间的定义。我将定义Car1
- Car1:首先汽车随机地置于一号门后
- <:主持人随机地执行如下的策略:打开最小编号的可允许的门。当这扇门既不包含车也不是竞赛者被选中的那扇门就称作是可允许的门。可替代的,主持人也已选择最高编号的可允许的门。
- Pick1:竞赛者选择了一号门。(不失一般性地)我们的采样空间只包含竞赛者只选中一号门的所有情形,对称地,如果竞赛者选中了二号门、三号门,将会得到同等的结果。
- Open2:听到了竞赛者的选择之后,根据既定的策略(在允许的门中根据或者最大编号或者最小编号),主持人打开了一扇门。本例中打开的是二号门。
我们会得到这一样本空间包含六个等概率输出:
M = {'Car1, 'Car1>Pick1/Open3',
'Car2, 'Car2>Pick1/Open3',
'Car3, 'Car3>Pick1/Open2' } 现在,我们假设竞赛者选中了一号门,主持人打开的是三号门。车在一号门背后的概率(也就是参赛者坚持原来的选择)?或者在二号门(也就是需要参赛者转变选择)?
P(T('Car1'), such_that(T('Open3'), M))输出是:
Fraction(1, 3)P(T('Car2'), such_that(T('Open3'), M))输出是:
Fraction(2, 3)我们看到从一号门转变到二号门有 2/3 的概率赢得该车,而坚持最开始的选择赢得汽车的概率只有 1/3 。所以相较山羊,你更喜欢汽车,你应该改变主意。但是难道你不感到难过吗如果你做出了错误的选择。这件事落到了Monty Hall自己身上,他打开了无数的门在主持Let’s Make a Deal的十三年间,竟然也不知道这一答案,直到被一封Monty写给统计学家Lawrence Denenberg的一封信中揭露出来,因为在此之前Denenberg层询问是否可以将这一问题应用到教科书中。

如果你是Denenberg,你会如何回复Monty用一种非数学化的术语。我会尝试做出如下的表达:
当竞赛者做出它最开始的选择,他获得车的概率是 1/3 ,车在另外两扇门后的概率是 2/3 。直到你打开了其中一扇门之前这些都是对的。在你打开一扇门(藏着山羊的)之后,均分在两扇门上的概率 2/3 就集中到了其中一扇门之后,竞赛者因此应该转变选择。
但是这一论据并不能说服所有人。Marilyn vos Savant 报道说她的很多读者(包括很多博士,这一点她也乐意指出)仍然坚持竞赛者无论转不转换选择和最后的答案都无关:几率都是 1/2 。我们试着去发现这些反对的人所处理的问题以及所采取的样本空间。也许他们的理由是这样的:
他们定义‘Car1/Pick1/Open2/Goat’形式的输出,这意味着:
- Car1:首先随机地将车置于某扇门的后面
- Pick1:竞赛者选中了一号门
- Open2:主持人随机地打开另外两扇门。(所以主持人有可能打开的是具有汽车的门)
- Goat:打开二号门后发现,2号门的后边是一只山羊。
在这一解释之下,样本空间变为:
M2 = {'Car1/Pick1/Open2/Goat', 'Car1/Pick1/Open3/Goat',
'Car2/Pick1/Open2/Car', 'Car2/Pick1/Open3/Goat',
'Car3/Pick1/Open2/Goat', 'Car3/Pick1/Open3/Car'}我们可以计算每一扇门背后的车的概率,在参赛者选中了一号门,主持人打开的是三号门且是一只山羊的条件之下:
P(T('Car1'), such_that(T('Open3/Goat'), M2))输出为:
Fraction(1, 2)P(T('Car2'), such_that(T('Open3/Goat'), M2))所以我们会看到在这一解释之下无论你转不转换选择都没有区别。
这是一个有效的解释吗?我同意问题的语言表达可能是有歧异的。然而,这一解释却存在一个严重的问题:在Let’s Make a Deal所播出的全部历史中,从来没有发生过主持人打开了一扇其后是车(或者其他的大奖)的门。这强烈说明(但不是严格的证明)M而不是M2是正确的样本空间。
非等概率输出:概率分布
迄今为止,我们做出的全部假设都是样本空间的所有输出值都是等概率发生的。在真实生活中,孩子是女孩(或者男孩)的概率并不严格等于 1/2 ,第二个孩子的性别并不完全独立于第一个孩子。一篇文章给出了丹麦所有两孩子的家庭统计数据:
GG:121801 GB:126840
BG:127123 BB:135138
我们将从输出值到频率值的映射称之为分布。如下是另两个定义:
- 分布:从样本空间中每一个输出值到频率的指定。
- 概率分布:一种被归一化为频率之和为1(每个频率介于0和1之间)的分布。
我们可以用dicts(python中的数据结构)来实现分布,代码如下:
ProbDist = dict
def probdist(**entries): return normalize(entries)
def normalize(dist):
total = sum(dist.values())
return { e: dist[e]/total for e in dist} DK = prodist(GG = 121801, GB = 126840,
BG = 127123, BB = 135138)
DK输出为:
{'BB': 0.2645086533229465,
'BG': 0.24882071317004043,
'GB': 0.24826679089140383,
'GG': 0.23840384261560926}现在让我们试着去修改函数P以及such_that来实现对样本空间或者概率分布的接受。
def P(event, space):
if callable(event):
event = such_that(event, space)
if isinstance(space, ProbDist):
return sum(space[e] for e in space if e in event)
return Fraction(len(event & space), len(space))
def such_that(predicate, space):
if isinstance(space, ProbDist):
return {e:space[e] for e in space if predicate(e)}
return {e for e in space if predicate(e)} 首先,我们来验证新的函数设计是否对样本空间是集合的原始问题依然适用12:
# 问题1,样本空间S
P(two_boys, such_that(older_is_boy, S))输出为:
Fraction(1, 2)# 问题2,样本空间S
P(two_boys, such_that(at_least_one_boy, S))输出为:
Fraction(1, 3)现在我们来看是否新定义能够适配概率分布DK。对问题1,我们期望的结果是略大于 1/2 ,对问题2,结果是略大于 1/3 。
# 问题1,样本空间变成了概率分布
P(two_boys, such_that(older_is_a_boy, DK))输出为:
0.5152805792702689# 问题2,样本空间变成了概率分布
P(two_boys, such_that(at_least_one_boy, DK))输出为:
0.34730828242538575一切工作良好。现在,我们来试着解决一个新问题,这一问题对基于集合的样本空间不再可行。
问题4。一个男孩生在2月29.两个都是男孩的概率?
- 问题4:我有两个孩子。至少有一个是男孩,且生在闰日,也就是2月29。问两个都是男孩的概率?假定男孩的出生率是 51.5 ,出生日均匀分布在4×365+1的四年的周期里13。
我们将使用记号GLBN这一记号来标识年长的女孩生在闰日,年幼的男孩生在一般的日子。我们需要定义一个辅助函数,joint,来创建两概率分布的联合概率密度。
def joint(A, B):
return {a + b: A[a]*B[b]
for a in A for b in B}
sexes = probhist(B = 51.5, G = 48.5)
days = prbhist(L = 1, N = 4*365)
child = joint(sexs, days)
S4 = joint(child, child)我们来检验最后两个的概率分布:
child输出为:
{'GL': 0.0003319644079397673,
'BL': 0.00035249828884325804,
'GN': 0.48466803559206023,
'BN': 0.5146475017111568}S4输出为:
{'BLGN': 0.00017084465320322452,
'BLGL': 1.1701688575563322e-07,
'GNBL': 0.00017084465320322452,
'GNGL': 0.00016089253748264833,
'BNGL': 0.00017084465320322455,
'GLGN': 0.00016089253748264833,
'BLBN': 0.00018141236371064048,
'BNBN': 0.2648620510175351,
'GNBN': 0.24943319367670783,
'GLBL': 1.1701688575563322e-07,
'BNGN': 0.24943319367670783,
'BLBL': 1.2425504363742498e-07,
'BNBL': 0.00018141236371064048,
'GNGN': 0.23490310472466655,
'GLGL': 1.1020036813880022e-07,
'GLBN': 0.00017084465320322455}其实这里我们已经把问题解决了。因为男孩生在闰日对应于很少的儿童,我们期望的两个儿童都是男孩的概率会略低于男孩出生率这一基线,也就是51.5%
boy_on_leap_day = T('BL')
P(two_boys, such_that(boy_on_leap_day, S4))输出为:
5149145040963757仿真
显式地定义一个样本空间并不总是方便的。有时样本空间是无限的,或者是很大且复杂的,我们有自信写出对这一问题的仿真程序,而不是对全部样本空间的枚举。对仿真的采样能够给出对概率值的精确估计。
例如,这里是对蒙提霍尔问题的一个仿真。给定一个布尔输入值标识参赛者是否选择转换门,函数monty(switch)返回True如果参赛者选中了汽车。
import random
from collections import Counter
def monty(switch = True):
doors = (1, 2, 3)
car = random.choice(doors)
pick = random.choice(doors)
opened = random.choice([d for d in doors if d != car and d != pick]
if switch:
pick = next(d for d in doors if d != pick and d != opened)
return pick == car我们之前便已确定,参赛者赢得汽车的概率是2/3如果转变选择,赢得汽车的概率只有1/3如果坚持最初的选择的话。
Counter(monty(switch = True) for _ in range(100000))输出为:
Counter({True: 66401, False: 33599})Counter(monty(switch = False) for _ in range(10000))输出为:
Counter({False: 66704, True: 33296})未完待续
原文地址请点击这里14。
sexes = probhist(B = 1, G = 1)
days = probhist(Y = 1, N = 6)
child = joint(sexes, days)
S = joint(child, child)
P(two_boys, such_that(T('BY'), S))|•|, cardinal number 基数的概念,表示集合的大小,也即集合中元素的个数; ↩- 在一般的编译环境中,
from __future__ import division要置于文件的头部,ipython notebook 则允许这样的结构; ↩ - filter的两个形参分别为function和list,用法为
filter(even, list(D)),不过这样做并无十分的必要,因为用集合表示样本空间是更为恰当的选择。注意在python3中,filter的返回值是一个filter object对象,想要遍历其中的元素,可使用__next__()成员函数。 ↩ - 这里P的函数形式(第一个形参为event集,第二个形参是某种条件下的集合,such_that可以嵌套)表示一种数学意义上的条件概率。 ↩
- 这里我们可以对比抛硬币实验,抛两次,其中至少有一个正面朝上,问:得到的两枚硬币都是正面朝上的概率|正正|/|正反, 反正, 正正| ↩
- Bertrand Russell 与本文的作者 Peter Novig是人工智能领域的经典教科书人工智能—一种现代方法的合作者。 ↩
- 这里我们可以按高中解排列组合的方法计算样本空间的大小。共有两个位置,每个位置上有14中可能情况,所以全部的情况是 142 种。 ↩
- 我们可以手工计算: 7+7−114+14−1=1327 ↩
- IPython + html标签 == IPython notebook。想要IPython显示html标签,需要IPython和浏览器进行交互,IPython notebook正是IPython和浏览器交互的一个强大的可视化工具。 ↩
- 极限思维法,这里的概率的范围是 (13,12) 。重叠区域最大时,概率值最小是1/3,重叠区域最小时,概率值得到最大1/2。 ↩
- 分析过这一问题(山羊、车、门),我可以继续探讨类似的随机选择排除一项错误答案的场景。比如电视台常见的答题节目:四选一,答题者首先选择一个选项(前提是答题者对问题毫无了解),然后主持人告知,他帮忙排除了余下一个错误选项,问他是否需要改变答案?同理也是应该的。道理在于坚持原来的选择正确的概率是 1/4 ,而如果在余下的两个选项中任选其一,正确的概率均是 3/8 。 ↩
- 显然依旧适用,只是对原始的P和such_that加了一个样本空间是否是分布的判断,如果不是,处理代码完全没变。 ↩
- 可以按照这里的处理手段(也就是基于概率分布而不是基于集合的样本空间) ↩
- 无耻地把原文地址放在文章的末尾。自己的翻译还离大师的原文差得很远。 ↩