神经网络的Python实现（二）全连接网络

在上一篇 神经网络的Python实现（一）了解神经网络 中，我们简单介绍了感知机模型和多层网络的基础结构。在这篇博文中，我们将使用python-numpy库搭建多层神经网络模型、介绍和实现BP算法。理论部分有部分参考。

更好的阅读效果，欢迎前往我的个人博客地址

全连接网络

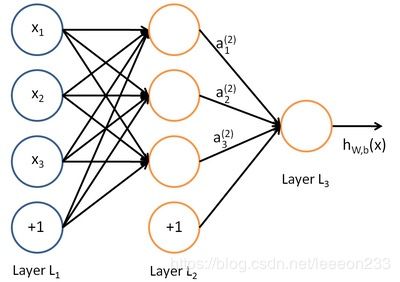
首先，简单介绍一下全连接网络(Fully-Connected Network)，即在多层神经网络中，第 $n$ 层的每个神经元都分别与第 $n-1$ 层的神经元相互连接。如下图便是一个简单的全连接网络：

我们使用圆圈来表示神经网络的输入，标上 $+1$ 的圆圈被称为偏置节点，也就是截距项。神经网络最左边的一层叫做输入层，最右的一层叫做输出层（上图中，输出层只有一个节点）。中间所有节点组成的一层叫做隐藏层，因为我们不能在训练样本集中观测到它们的值。同时可以看到，以上神经网络的例子中有3个输入单元（偏置单元不计在内），3个隐藏单元及一个输出单元。

我们用 $n_l$ 来表示网络的层数，上图例子中 $n_l=3$ ，我们将第 $ l $ 层记为 $L_l$ ，于是 $L_1$ 是输入层，输出层是 $L_{n_l}$ 。本例神经网络有参数 $(W,b)=(W^{(1)},b^{(1)},W^{(2)},b^{(2)})$ ，其中 $W_{ij}^{(l)}$ 是第 $l$ 层第 $j$ 单元与第 $l+1$ 层第 $i$ 单元之间的联接参数（其实就是连接线上的权重，注意标号顺序）， $b_i^{(l)}$ 是第 $l+1$ 层第 $i$ 单元的偏置项。因此在本例中， $W^{(1)}\in {\Re }^{3\times 3}$ ， $W^{(2)}\in {\Re }^{1\times 3}$ 。注意，没有其他单元连向偏置单元(即偏置单元没有输入)，因为它们总是输出 $+1$。同时，我们用 $s_l$ 表示第 $l$ 层的节点数（偏置单元不计在内）。

接下来详细介绍神经网络的前向和反向的计算过程。

前向传播

我们用 $a_i^{(l)}$ 表示第 $l$ 层第 $i$ 单元的激活值（输出值）。当 $l=1$ 时， $a_i^{(1)}=x_i$ ，也就是第 $i$ 个输入值（输入值的第 $i$ 个特征）。对于给定参数集合 $W,b$ ，我们的神经网络就可以按照函数 $h_{W,b}(x)$ 来计算输出结果。本例神经网络的计算步骤如下：

$$\begin{array}{rl}{a}_1^{(2)}& =f(W_{11}^{(1)}{x}_1+W_{12}^{(1)}{x}_2+W_{13}^{(1)}{x}_3+b_1^{(1)})\\ a_2^{(2)}& =f(W_{21}^{(1)}{x}_1+W_{22}^{(1)}{x}_2+W_{23}^{(1)}{x}_3+b_2^{(1)})\\ a_3^{(2)}& =f(W_{31}^{(1)}{x}_1+W_{32}^{(1)}{x}_2+W_{33}^{(1)}{x}_3+b_3^{(1)})\\ h_{W,b}(x)& =a_1^{(3)}=f(W_{11}^{(2)}{a}_1^{(2)}+W_{12}^{(2)}{a}_2^{(2)}+W_{13}^{(2)}{a}_3^{(2)}+b_1^{(2)})\end{array}$$

我们用 $z_i^{(l)}$ 表示第 $l$ 层第 $i$ 单元输入加权和（包括偏置单元），比如， $$z_i^{(2)}=\sum _{j=1}^n{W}_{ij}^{(1)}{x}_j+b_i^{(1)}$$ 则 $$a_i^{(l)}=f(z_i^{(l)})$$

这样我们就可以得到一种更简洁的表示法。这里我们将激活函数 $f(\cdot )$ 扩展为用向量（分量的形式）来表示，即 $f([z_1,z_2,z_3])=[f(z_1),f(z_2),f(z_3)]$ ，那么，上面的等式可以更简洁地表示为：

$$\begin{array}{rl}{z}^{(2)}& =W^{(1)}x+b^{(1)}\\ a^{(2)}& =f(z^{(2)})\\ z^{(3)}& =W^{(2)}{a}^{(2)}+b^{(2)}\\ h_{W,b}(x)& =a^{(3)}=f(z^{(3)})\end{array}$$

我们将上面的计算步骤叫作前向传播。回想一下，之前我们用 $a^{(1)}=x$ 表示输入层的激活值，那么给定第 $l$ 层的激活值 $a^{(l)}$ 后，第 $l+1$ 层的激活值 $a^{(l+1)}$ 就可以按照下面步骤计算得到：

$$\begin{array}{rl}{z}^{(l+1)}& =W^{(l)}{a}^{(l)}+b^{(l)}\\ a^{(l+1)}& =f(z^{(l+1)})\end{array}$$
将参数矩阵化，使用矩阵－向量运算方式，我们就可以利用线性代数的优势对神经网络进行快速求解。

# 在python 3 numpy 中，矩阵相乘可以使用 a @ b
z = activation(a @ w + b)

激活函数

在上面例子中 $f(\cdot )$ 便是激活函数，是神经网络中十分重要的一环。若没有激活函数，那么神经网络的输出便始终只是各个输入的线性组合。“深度”起不到作用。
所以激活函数的作用便是加入某种非线性的映射。早期经常使用的是Sigmoid函数，近几年多使用ReLU函数及其变体。下面介绍一下常见的激活函数及其导数。

1. sigmoid

数学形式：

$$\begin{array}{rl}f(z)& =\frac{1}{1+e^{-z}}\\ & \\ f^{\prime }(z)& =(\frac{1}{1+e^{-z}}{)}^{\prime }=\frac{e^{-z}}{(1+e^{-z}{)}^2}\\ & \\ & =\frac{1+e^{-z}-1}{(1+e^{-z}{)}^2}=\frac{1}{(1+e^{-z})}(1-\frac{1}{(1+e^{-z})})\\ & \\ & =f(z)(1-f(z))\end{array}$$

Sigmoid函数会将输入映射到(0,1)的范围，较大的值会被映射为1，较小的值会被映射为0。直观上符合神经元活跃与抑制状态的区分。

缺点：

1. 如图，输入值的绝对值在4以上的情况下就基本趋于饱和了，达到1或0。在反向传播时，会造成由于梯度过小而产生权重更新缓慢甚至梯度消失。并且初始化权重时不可太大。
2. Sigmoid函数的输出分布不是以0为中心分布的，在梯度下降过程中可能会存在梯度恒正或是恒负的情况出现。

import numpy as np

def sigmoid(z):
  return 1.0 / (1.0 + np.exp(-x))
  
def sigmoid_prime(z):
  return sigmoid(z) * (1 - sigmoid(z))

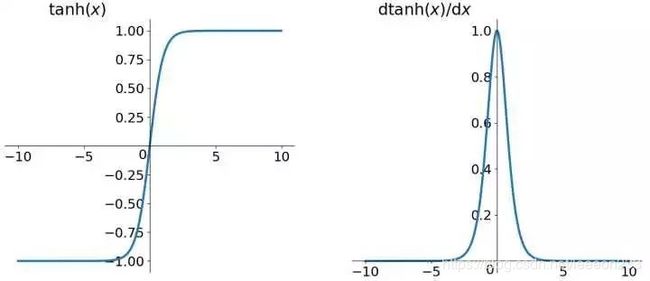
2. tanh

数学形式：
$$\begin{array}{rl}f(z)& =\tanh (z)=\frac{\sinh (z)}{\cosh (z)}=\frac{e^z-e^{-z}}{e^z+e^{-z}}\\ & \\ f^{\prime }(z)& =\frac{{\cosh }^2(z)-{\sinh }^2(z)}{{\cosh }^2(z)}=1-f^2(z)\end{array}$$

tanh函数会将输入映射到[-1,1]的范围，较大的值会被映射为1，较小的值会被映射为-1。

缺点：类似于Sigmoid函数，也具有一定的激活饱和性。

import numpy as np

def tanh(z):
  return np.tanh(z)
  
def tanh_prime(z):
  return 1 - np.square(tanh(z))

3. relu

数学形式

$$\begin{array}{rl}f(z)& =\max (0,z)\\ & \\ f^{\prime }(z)& =\{\begin{array}{ll}0& \text{z <= 0}\\ 1& \text{z > 0}\end{array}\end{array}$$

优点：

1. 计算速度快。求导简单。
2. 不再梯度弥散。ReLU函数不像Sigmoid函数，不存在梯度饱和区，几乎不会造成梯度弥散。
3. 减少过拟合。部分神经元输出可能为0，加大网络稀疏性，减少过拟合。

缺点：初始化不佳会造成神经元死亡。针对此问题提出了Leaky ReLU、PReLU和RReLU等变体。

import numpy as np

def relu(z):
  return (np.abs(z) + z) / 2
  
def relu_prime(z):
  return np.where(z > 0, 1, 0)
  

损失函数

当我们的输入数据经过神经网络，得到了一组输出数据。我们想去衡量我们的模型的好坏、给我们的模型一个得分或者说是我们想要优化的最终目标，便需要定义好损失函数。将我们的输出值与真实值通过损失函数进行计算，得到损失值(loss)，为了使得模型更好，能够与真实情况相拟合，所以我们需要找到一个适合的网络权重使得输出的loss最小。对于回归问题最常使用的损失函数是均方误差(Mean-Square Error,MSE)，对于分类问题最常使用的是交叉熵(Cross Entropy),这里仅简单介绍MSE。

$$MSE=\frac{1}{N}\sum _{i=1}^N(y_i-\widehat{y_i}{)}^2$$

均方误差是指参数估计值与参数真值之差平方的期望值;
MSE可以评价数据的变化程度，MSE的值越小，说明预测模型描述实验数据具有更好的精确度。

反向传播

现在我们已经了解了全连接神经网络的前向传播和激活函数和其导数的数学表达，下面我们要使用反向传播算法进行最优参数(采用梯度下降法，可能造成局部最优)的求解。

由于神经网络结构十分复杂，想要直接去求得权重的最优解是不大可能的。所以采用迭代的思想进行一步一步的权重更新，直到找到最佳的解。最常用的便是梯度下降法(gradient descent)。如果不了解梯度下降法，推荐观看Andrew Ng的机器学习视频。

接下来假设你已经了解梯度下降法，现在我们来一起推导一下反向传播算法的公式，了解整个过程。这里采用下图简单的例子作为示范。很容易地可以扩展到任意宽度，任意深度的全连接网络上去。

假设我们的神经网络是一个输入层，有两个神经元；一个隐藏层，有两个神经元；一个输出层，有一个神经元。从图可以看到一共有6个权重需要我们计算。

说明：接下来的激活函数都是sigmoid函数，均以 f(·) 表示。小写字母表示未经激活函数的输出，大写字母表示通过激活函数的输出值。

隐藏层到输出层

数据通过神经网络得到了一个输出 $\hat{y}$ ，我们定义的损失函数为MSE，所以可以计算出当前的loss作为总误差(这里举例为一个输出神经元，如果有多个输出，总误差加和即可)。最后输出层这里我们不添加激活函数,所以 $\hat{y}=O_1$ 。

$$E=\frac{1}{2}{\left(y-\hat{y}\right)}^2=\frac{1}{2}{\left(y-O_1\right)}^2$$

有了总误差，接下来我们就可以通过梯度下降法进行权重的更新。先来看隐藏层到输出层的权重 $w_5,w_6$ 。

找到在前向传播时，有关 $w_5,w_6$ 的式子：

$$\begin{array}{rl}{O}_1& =f(o_1)\\ o_1& =w_5{H}_1+w_6{H}_2+b_h\end{array}$$

根据链式法则求出 $w_5,w_6$ 对于总误差的偏导：

$$\begin{array}{rl}\frac{\partial E}{\partial w_5}& =\frac{\partial E}{\partial O_1}\ast \frac{\partial O_1}{\partial o_1}\ast \frac{\partial o_1}{\partial w_5}\\ & =-(y-o_1)\ast f^{\prime }(o_1)\ast H_1\\ & =-(y-o_1)\ast f(o_1)\ast \left(1-f(o_1)\right)\ast H_1\end{array}$$

同理可得：

$$\begin{array}{rl}\frac{\partial E}{\partial w_6}& =\frac{\partial E}{\partial O_1}\ast \frac{\partial O_1}{\partial o_1}\ast \frac{\partial o_1}{\partial w_6}\\ & =-(y-o_1)\ast f^{\prime }(o_1)\ast H_2\\ & =-(y-o_1)\ast f(o_1)\ast \left(1-f(o_1)\right)\ast H_2\end{array}$$

对于偏置项 $b_h$：

$$\begin{array}{rl}\frac{\partial E}{\partial b_h}& =\frac{\partial E}{\partial O_1}\ast \frac{\partial O_1}{\partial o_1}\ast \frac{\partial o_1}{\partial b_h}\\ & =-(y-o_1)\ast f^{\prime }(o_1)\\ & =-(y-o_1)\ast f(o_1)\ast \left(1-f(o_1)\right)\end{array}$$

为了方便表示，我们把来自 $o_1$ 的误差表示为 $\delta o_1$，即：
$$\delta o_1=\frac{\partial E}{\partial O_1}\ast \frac{\partial O_1}{\partial o_1}=-(y-o_1)\ast f(o_1)\ast \left(1-f(o_1)\right)$$
整理后得到：

$$\begin{array}{rl}{\delta }_{w_5}& =\frac{\partial E}{\partial w_5}=\delta o_1\ast H_1\\ {\delta }_{w_6}& =\frac{\partial E}{\partial w_6}=\delta o_1\ast H_2\\ {\delta }_{b_h}& =\frac{\partial E}{\partial b_h}=\delta o_1\end{array}$$

我们计算出来 $w_5.w_6,b_h$ 的偏导之后，就可以进行权重的更新了。（这里并不立刻更新，因前层进行反向传播时需要此层更新前的权重，下面会讲）
$$\begin{gathered} w_5\leftarrow w_5+\eta \nabla {\delta }_{w_5} \\ {w}_6\leftarrow w_6+\eta \nabla {\delta }_{w_6} \\ {b}_h\leftarrow b_h+\eta \nabla {\delta }_{b_h} \end{gathered}$$

这里的 $\eta$为学习率。

输入层到隐藏层

与隐藏层到输出层类似，只不过有小小的差别。
对于 $w_1,w_2,w_3,w_4,b_i$ ，只拿 $w_1$ 作为示范，其他的类似求解。

首先列出前向传播时与 $w_1$ 有关的公式：

$$\begin{array}{rl}{O}_1& =f(o_1)\\ o_1& =w_5{H}_1+w_6{H}_2+b_h\\ H_1& =f(h_1)\\ h_1& =w_1{x}_1+w_3{x}_2+b_i\end{array}$$

从上式可以看出，我们需要先求出$H_1$处的误差，进而求得 $w_1$ 的梯度。

$$\begin{array}{rl}\frac{\partial E}{\partial H_1}& =\frac{\partial E}{\partial O_1}\ast \frac{\partial O_1}{\partial o_1}\ast \frac{\partial o_1}{\partial H_1}\\ & =\delta o_1\ast w_5\end{array}$$

这里便是上面提到的需要使用更新前的隐藏层到输出层的权重值

接下来便和隐藏层到输出层的反向传播没有差别了，以 $w_1$ 为例：

$$\begin{array}{rl}\frac{\partial E}{\partial w_1}& =\frac{\partial E}{\partial H_1}\ast \frac{\partial H_1}{\partial h_1}\ast \frac{\partial h_1}{\partial w_1}\\ & =(\delta o_1\ast w_5)\ast \left(f(h_1)\ast \left(1-f(h_1)\right)\right)\ast x_1\end{array}$$

其他的权重和偏置项也根据公式进行类似的计算，并进行更新。

至此反向传播便完成了，全部的权重得到了更新。下面我们根据上面的过程来编写代码。

CODE

Layer类

因为预计还要将CNN、RNN、LSTM等都采用numpy实现一遍，所以我们先定义一个Layer的基类。里面写一些，所有层都需要的函数，比如激活函数等。这里API形式仿照Keras。

from abc import abstractmethod
import numpy as np

class Layer(object):
    def _activation(self, name, x):
        """
        激活函数
        :param name: 激活函数的名称。
        :param x:    激活函数的自变量。
        :return:     返回激活函数计算得到的值
        """
        if name == 'sigmoid':
            return 1.0 / (1.0 + np.exp(-x))
        elif name == 'tanh':
            return np.tanh(x)
        elif name == 'relu':
            return (np.abs(x) + x) / 2
        elif name == 'none':   # 不使用激活函数
            return x
        else:
            raise AttributeError("activation name wrong")

    def _activation_prime(self, name, x):
        if name == 'sigmoid':
            return self._activation(name, x) * (1 - self._activation(name, x))
        elif name == 'tanh':
            return 1 - np.square(self._activation(name, x))
        elif name == 'relu':
            return np.where(x > 0, 1, 0)
        elif name == 'none':
            return 1
        else:
            raise AttributeError("activation name wrong")
            
    @abstractmethod
    def forward_propagation(self, **kwargs):
        pass

    @abstractmethod
    def back_propagation(self, **kwargs):
        pass

Dense层

接下来我们开始编写Dense层。

from Layer import Layer
import numpy as np

class DenseLayer(Layer):
    def __init__(self, shape, activation, name):
        """
        Dense层初始化。
        :param shape:       如输入神经元有2个，输出神经元有3个。那么shape = (2,3)
        :param activation:  激活函数名称
        :param name:        当前层的名称
        """
        super().__init__()
        self.shape = shape
        self.activation_name = activation
        self.__name = name
        self.__w = 2 * np.random.randn(self.shape[0], self.shape[1]) # 这里采用矩阵的随机初始化
        self.__b = np.random.randn(1, shape[1])                      

    def forward_propagation(self, _input):
        """
        Dense层的前向传播实现
        :param _input: 输入的数据，即前一层的输出
        :return:       通过激活函数后的输出
        """
        self.__input = _input
        self.__output = self._activation(self.activation_name, self.__input.dot(self.__w) + self.__b)
        return self.__output

    def back_propagation(self, error, learning_rate):
        """
        Dense层的反向传播
        :param error:           后一层传播过来的误差
        :param learning_rate:   学习率
        :return:                传播给前一层的误差
        """
        o_delta = np.matrix(error * self._activation_prime(self.activation_name, self.__output))
        w_delta = np.matrix(self.__input).T.dot(o_delta)
        input_delta = o_delta.dot(self.__w.T)
        self.__w -= w_delta * learning_rate
        self.__b -= o_delta * learning_rate
        return input_delta

Model类

接着写一个Model类实现Keras的各种API

import numpy as np


class Model(object):
    def __init__(self):
        """
        简单使用列表按顺序存放各层
        """
        self.layers = []

    def add(self, layer):
        """
        向模型中添加一层
        :param layer:  添加的Layer
        """
        self.layers.append(layer)

    def fit(self, X, y, learning_rate, epochs):
        """
        训练
        :param X:                   训练集数据
        :param y:                   训练集标签
        :param learning_rate:       学习率
        :param epochs:              全部数据集学习的轮次
        """
        if self.__loss_function is None:
            raise Exception("compile first")
        # 前馈
        for i in range(epochs):
            loss = 0
            for num in range(len(X)):
                out = X[num]
                for layer in self.layers:
                    out = layer.forward_propagation(out)
                loss += self.__loss_function(out, y[num], True)
                error = self.__loss_function(out, y[num], False)

                for j in range(len(self.layers)):
                    index = len(self.layers) - j - 1
                    error = self.layers[index].back_propagation(error, learning_rate)
            print("epochs {} / {}  loss : {}".format(i + 1, epochs, loss/len(X)))

    def compile(self, loss_function):
        """
        编译，目前仅设置损失函数
        :param loss_function:  损失函数的名称
        """
        if loss_function == 'mse':
            self.__loss_function = self.__mse

    def __mse(self, output, y, forward):
        """
        :param output:      预测值
        :param y:           真实值
        :param forward:     是否是前向传播过程
        :return:            loss值
        """
        if forward:
            return np.squeeze(0.5 * ((output - y) ** 2))
        else:
            return output - y

    def predict(self, X):
        """
        结果预测
        :param X: 测试集数据
        :return:  对测试集数据的预测
        """
        res = []
        for num in range(len(X)):
            out = X[num]
            for layer in self.layers:
                out = layer.forward_propagation(out)
            res.append(out)
        return np.np.squeeze(np.array(res))

Main

最后我们来写一个主函数简单拟合异或测试一下全连接网络。

from Dense import DenseLayer
import Model

if __name__ == '__main__':
    model = Model.Model()
    X = np.array([
      [1, 1],
      [1, 0],
      [0, 1],
      [0, 0]
    ])
    y = np.array([0, 1, 1, 0])
    model.add(Dense((2, 3), 'sigmoid', 'dense1'))
    model.add(Dense((3, 4), 'sigmoid', 'dense2'))
    model.add(Dense((4, 1), 'none', 'output'))
    model.compile('mse')
    model.fit(X, y, 0.1, 1000)
    print(model.predict([[1, 1], [1, 0]]))

epochs 1 / 1000 loss : 1.5461586301292716
epochs 2 / 1000 loss : 1.0010336204321242
epochs 3 / 1000 loss : 0.8421754635331838
epochs 4 / 1000 loss : 0.7311597301044074
epochs 5 / 1000 loss : 0.6428097142979868
epochs 6 / 1000 loss : 0.5709843947151808
epochs 7 / 1000 loss : 0.5122654038390013
epochs 8 / 1000 loss : 0.4640985740577866
epochs 9 / 1000 loss : 0.4244527616264729
epochs 10 / 1000 loss : 0.39169518752811794
···
epochs 995 / 1000 loss : 0.0018694401858458181
epochs 996 / 1000 loss : 0.0018245697992101736
epochs 997 / 1000 loss : 0.001780665685232114
epochs 998 / 1000 loss : 0.0017377108735277388
epochs 999 / 1000 loss : 0.0016956885636446625
epochs 1000 / 1000 loss : 0.001654582127688094
···
[0.0610148 0.98877437]

可见模型是能够收敛，并且拟合非线性映射的。

如果你有某些疑问或是改进，欢迎留下你的评论。

TODO

现在我们实现了全连接神经网络，在下一篇博文我们将会继续推导和实现最为常用而且是最为复杂的卷积神经网络（CNN）。