线性回归之梯度下降（bgd）

线性模型：

 y=ωT∗x+b   y = ω T ∗ x + b

线性回归是假设数据满足以上的线性假设，其中w和x是一个向量，y和b是一个实数。

 y=ω1x1+ω2x2+ω2x2+⋯+ω3x3+ωnxn+b   y = ω 1 x 1 + ω 2 x 2 + ω 2 x 2 + ⋯ + ω 3 x 3 + ω n x n + b

跟以上这个方程式是等价的。

loss=∑i=0n(yi−y^)2=∑i=0n(ωTxi+b−y^i)2 l o s s = ∑ i = 0 n ( y i − y ^ ) 2 = ∑ i = 0 n ( ω T x i + b − y ^ i ) 2

显然，我们事先是不知道w和b取什么值是最好的。但是，我们知道，如果定义一个损失函数（就是上面的这个公式），当取到的w和b，使得损失函数的值最少时，这个w和b就是最好的。换句话说，当我们手上有足够多的一堆 (x⃗ 1,y1),(x⃗ 2,y2),… ( x → 1 , y 1 ) , ( x → 2 , y 2 ) , … 的事先已经标注好的数据，我们就能通过损失函数来寻找到 ω⃗ ,b ω → , b 。这样，我们将一个优化问题，转化为学习问题。

很明显的，这个线性回归的问题在高中就已经研究过了，当时使用的是最小二乘法，但我们现在要使用的是梯度下降方法bgd。这种方法可谓是所有优化方法中最基本的一个，适用场景非常广泛，而且实现也很简单。到目前为止，深度学习的主流方法依然是离不开梯度下降，其他优化算法也只是梯度下降的变种而已。

梯度下降（bgd）

让我们先将线性回归的问题再简化一下，假设x只是一个实数，有没有偏置，也就是说 y=ωx y = ω x 那么loss就会是：

loss=∑i=1n(yi−y^i)2=∑i=1n(ωxi−y^i)2 l o s s = ∑ i = 1 n ( y i − y ^ i ) 2 = ∑ i = 1 n ( ω x i − y ^ i ) 2

很显然，公式中 xi,yi x i , y i 都是常数。 只有w是未知变量，那么loss就是一个关于w的二次函数而已。我们要求loss的最小值时的w，相当于求二次函数的最低点。
高中的方法就是一步到位，直接算出二次函数中导数为0的点，这个点就是最小值点。

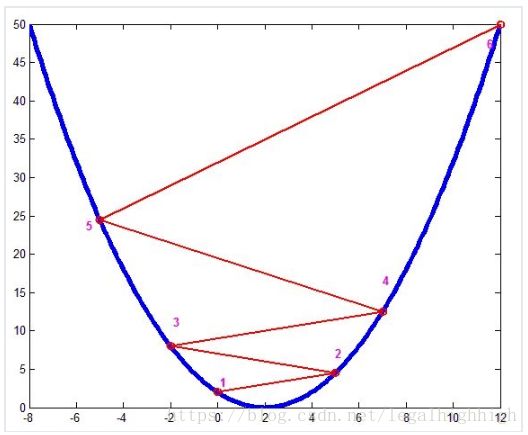
梯度下降的方法是，首先，任意取一点w，然后算出该点w的导数，如果导数大于0，那就往w轴的负方向走，如果导数少于0，那就往w轴的正方向走。那么经过多步迭代后，我们总能走到最值点的附近。

loss′(ω)=2∑i=1n(ωxi−y^i)xi l o s s ′ ( ω ) = 2 ∑ i = 1 n ( ω x i − y ^ i ) x i

ωn+1=ωn−ηloss′(ω) ω n + 1 = ω n − η l o s s ′ ( ω )

上面这个公式，任意去一个点 ω ω ，然后计算 ω ω 的倒数 loss′(ω) l o s s ′ ( ω ) ,根据学习率 η η 与导数相乘，就能得到新的一点 ω ω 。而对于线性回归也是一样的思路：

 y=ωT∗x+b   y = ω T ∗ x + b

loss=∑i=0n(yi−y^)2=∑i=0n(ωTxi+b−y^i)2 l o s s = ∑ i = 0 n ( y i − y ^ ) 2 = ∑ i = 0 n ( ω T x i + b − y ^ i ) 2

只不过用的不是导数，而是偏导数：

∂loss∂ω1=2∑i=1n(ωxi−y^i)xi1 ∂ l o s s ∂ ω 1 = 2 ∑ i = 1 n ( ω x i − y ^ i ) x i 1

ωn+11=ωn1−η∂lossω1 ω 1 n + 1 = ω 1 n − η ∂ l o s s ω 1

∂loss∂ω2=2∑i=1n(ωxi−y^i)xi2 ∂ l o s s ∂ ω 2 = 2 ∑ i = 1 n ( ω x i − y ^ i ) x i 2

ωn+12=ωn2−η∂lossω2 ω 2 n + 1 = ω 2 n − η ∂ l o s s ω 2

⋯ ⋯

∂loss∂b=2∑i=1n(ωxi−y^i) ∂ l o s s ∂ b = 2 ∑ i = 1 n ( ω x i − y ^ i )

bn+1=bn−η∂lossb b n + 1 = b n − η ∂ l o s s b

以此类推，代码如下：

import numpy as np
import math 

# 普通的全梯度下降方法

sample = 10
num_input = 5

#加入训练数据
normalRand = np.random.normal(0,0.1,sample)
weight = [7,99,-1,-333,0.06]
x_train = np.random.random((sample, num_input))
y_train = np.zeros((sample,1))
for i in range (0,len(x_train)):
    total = 0
    for j in range(0,len(x_train[i])):
        total += weight[j]*x_train[i,j]
    y_train[i] = total+normalRand[i]

# 训练
weight = np.random.random(num_input+1)
rate = 0.05

for epoch in range(0,100):

    # 计算loss
    predictY = np.zeros((len(x_train,)))
    for i in range(0,len(x_train)):
        predictY[i] = np.dot(x_train[i],weight[0:num_input])+weight[num_input]
    loss = 0
    for i in range(0,len(x_train)):
        loss += (predictY[i]-y_train[i])**2
    print("epoch: %d-loss: %f"%(epoch,loss))

    # 计算梯度并更新
    for i in range(0,len(weight)-1):
        grade = 0
        for j in range(0,len(x_train)):
            grade += 2*(predictY[j]-y_train[j])*x_train[j,i]
        weight[i] = weight[i] - rate*grade

    grade = 0
    for j in range(0,len(x_train)):
        grade += 2*(predictY[j]-y_train[j])
    weight[num_input] = weight[num_input] - rate*grade

print(weight)

做实验时，很容易发现，学习速率 η η 过大，损失函数不收敛，过小，收敛速度很慢。
github地址：代码