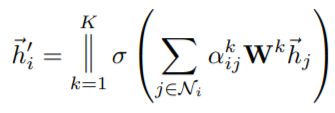【GNN】图注意力网络GAT(含代码讲解)

毫无疑问，图神经网络(Graph Neural Networks)是泛计算机视觉领域内继CNN、GAN、NAS等之后的又一个研究热点，非常的powerful。

图神经网络通俗来讲，适用于图类数据的神经网络。通常分为频域(spectral domain)和空域(vertex domain)两个派别，注意这两个派别都有非常优秀的模型存在。所以，并不要歧视其中的某个派别。

对于信号和线代忘得差不多的同学，想从一般神经网络入门GNN的话。我非常建议从空域入手。各大GCN解析博文中，都是拉普拉斯矩阵、傅里叶变换起步，对新手是非常unfriendly的。我认为入门GNN的第一篇论文千万不能读GCN，不然你很容易主动放弃的。

GAT是空域GNN的代表模型，Bengio大佬团队出品，发表在ICLR2018，目前谷歌引用已经一千了。它的特点是，很适合作为上手GNN模型。

闲话不多扯，按照国际惯例，先给出论文标题和链接：

标题：Graph attention networks

原文链接：https://arxiv.org/pdf/1710.10903.pdf

keras(推荐)：https://github.com/danielegrattarola/keras-gat

pytorch: https://github.com/Diego999/pyGAT

推荐keras版本，其注释非常准确，与论文可直接对应。

---

Graph attention networks

图注意力网络的重点非常明显，那就是attention。这个attention就是图中每个node相对于其相邻节点的相互重要性。

图神经网络的两大主要功能是：节点分类和图分类。

本文以节点分类来举例。

1. 图数据

我们先了解一下图数据：一系列带连接的节点，每个节点还有自己的特征。

上面这个五饼状的东西就是一个无向连接的图数据了。我们把这个图叫作G，G含有5个节点(node)，然后每个节点都有其邻节点(即节点之间有连接(edge))，除此之外，每个节点还有它的feature(可以是一个数值、向量或者矩阵)。

 , 其中代表的就是第i个节点的特征。

我们可以获得G的邻接矩阵(Adjacent matrix) A：(式0)

0 1 0 0 0
1 0 1 0 1
0 1 0 1 0
0 0 1 0 1
0 1 0 1 0

这个邻接矩阵A应该特别好理解吧，，表示1号节点跟2号节点有连接。该矩阵有3个特性：

1， 全部由0和1组成，1表示有连接，0表示无连接；

2，对角线元素为0，因为自己跟自己是没有连接的。当然，有些图的节点是允许自己连接自己的，这个时候对角线的元素可以不为0；

3，邻接矩阵是一个对称矩阵。

对于无向图数据来讲，邻接矩阵足以表达该图的结构特征。前面说到，图数据除了结构特征之外，还有节点特征。本文中的节点特征为一个F维的向量。举个栗子，假设F=3，那么节点特征可以为[1, 2, 3]。对于G来讲，5个节点，每个节点都含有一个F维的向量。

好了，咱们的图神经网络处理的就是上述的图数据了。

2. 图注意力网络

图注意力网络英文全称为Graph attention networks。按理来说，其缩写应该是GAN，可惜这个网名被生成式对抗网络先用了。无奈只能叫GAT，有点像山寨版的网络。但这丝毫不影响其作为一种强势GNN的存在。

前面提到，GAT是一种空域的GNN。什么是空域，什么又是频域？

简单地说，空域是从空间上考虑图结构的模型，即考虑目标节点和其他节点的几何关系(有无连接)。频域的代表算法是GCN，它就会对图邻接矩阵做一些加工，然后对其进行特征分解，得到特征值，将特征向量看作常数，而卷积核作用在特征值上。在我看来，频域的好处之一是可以省很多参数，但其缺点是不太容易作用于动态图。比如，某个图在不同时刻可能会多或者少俩节点，多或者少俩连接，这样特征向量就会发生改变，所以频域GNN不太能很好适应。

but，GAT这类的空域GNN能够完美应对动态图。且看GAT的详细分析：

1. 图注意力层

高端的食材往往只需最简单的烹饪方式，高端的模型也是如此，它只需简单的堆层就可以构成。GAT只需堆图注意力层就可以了，所以理解GAT只需理解图注意力层即可。

图注意力层，在文中描述为"Graph Attentional Layer"。我在下文中会简称为GAL。

我们先理解何为注意力(attention)，我们继续看这张图：

对于节点3，它的邻接节点只有节点2和节点4，但不代表这两个节点对节点3具有一样的重要性。这个“重要性”可以进行量化，更可以通过网络训练得出。这个“重要性”，在文中叫attention，可以通过训练得到。这便是GAT的核心创新点了。

这个attention是不满足对称性(后面会证明)，即节点2对节点3的attention与节点3对节点2的attention是不一样的，把每个连接(edge)当成桥的话，这个attention类似桥的宽度。当然，简化版的GAT中可以使这个attention变得对称。

整个论文的数学讨论就在于如何训练attention，以及将attention融入图神经网络中。

我们直接看一个核心公式：

这个公式和论文中的公式(2)和公式(3)是对应的，我只是转化成了用更直观的形式。表示节点i和节点j之间的attention系数，咱们由内向外看看这个公式。

首先权重矩阵W，是一个FxF’形状的矩阵。F表示输入节点特征的维数，而F'表示该层输出节点的维数。而其中的和表示，节点i和节点j的节点特征，如果这层GAL为输入层，那么节点特征直接就是图的原节点特征x。注意这里为什么用h而不用x，意思是表达这个节点特征会随着层的堆叠而改变，所以用h来表示隐藏层特征hidden feature。通过前面的描述，应该不难看出的维度是1xF吧。通过线代的知识，我们轻易知道的维度为1xF'。

重点是那个双竖线"||"，这个符号在文中代表concatenate，表示张量的粘合。张量的粘合就是，[[1， 2], [3，4]]粘合[[5, 6], [7, 8]]变成[[1， 2], [3，4]，[5, 6], [7, 8]]。这个栗子很形象吧，但是不同维度进行concatenate的效果是不一样的，详情请看我另一篇文章《tf.concat详解》。

通过concat，我们把两个1xF'的张量粘合成了1x2F'的大张量。然后乘以一个2F'x1的attention kernel ，这样不就可以得到1个数么，这个数就是未加工的attention系数。用图来解释这个过程会非常直观，这里取F'=4：

表示激活函数，这里用的是leaky ReLU(负倾斜率=0.2)。leaky relu不明白的百度一下，1分钟你就能明白。

最后再加一层softmax，不明白softmax的请戳《详解softmax》。

在这里我们思考一下，如果在上面公式中将节点i和节点j兑换位置，即i对于j的attention，是否会输出不同结果呢？

答案：是的。在论文中的attention是不满足对称性的。

看看keras代码实现，来自上面分享的Daniele大神的代码:

for head in range(self.attn_heads):
    kernel = self.kernels[head]  # W in the paper (F x F')
    attention_kernel = self.attn_kernels[head]  # Attention kernel a in the paper (2F' x 1)
    # Compute inputs to attention network
    features = K.dot(X, kernel)  # (N x F')

    # Compute feature combinations
    # Note: [[a_1], [a_2]]^T [[Wh_i], [Wh_2]] = [a_1]^T [Wh_i] + [a_2]^T [Wh_j]
    attn_for_self = K.dot(features, attention_kernel[0])    # (N x 1), [a_1]^T [Wh_i]
    attn_for_neighs = K.dot(features, attention_kernel[1])  # (N x 1), [a_2]^T [Wh_j]

    # Attention head a(Wh_i, Wh_j) = a^T [[Wh_i], [Wh_j]]
    dense = attn_for_self + K.transpose(attn_for_neighs)  # (N x N) via broadcasting

    # Add nonlinearty
    dense = LeakyReLU(alpha=0.2)(dense)

    # Mask values before activation (Vaswani et al., 2017)
    mask = -10e9 * (1.0 - A)
    dense += mask

    # Apply softmax to get attention coefficients
    dense = K.softmax(dense)  # (N x N)

其实代码跟论文还是有些许不同的，主要是为了方便计算。我们看到这里有个for循环，表示attention heads，这个点我们先hold，我在后文中会讲这个attention heads。

在代码中，把一个2F'x1的attention kernel当作两个F'x1的小kernel，一个负责自注意力，一个负责邻节点注意力。通过用这两个小kernel分别对和相乘，就能得到两个Nx1的张量，即自注意力指标和邻注意力指标。假设获得的自注意力指标我sa={1, 2, 3, 4, 5}，而获得的邻注意力指标na为{a, b, c, d, e}。将其扩充到二维，即sa+na.T，可得到一张二维表格：

a+1	a+2	a+3	a+4	a+5
b+1	b+2	b+3	b+4	b+5
c+1	c+2	c+3	c+4	c+5
d+1	d+2	d+3	d+4	d+5
e+1	e+2	e+3	e+4	e+5

我们再用前面的邻接矩阵A，请看式0，做一下mask进行过滤，即邻接矩阵A中元素为0的位置，将其注意力系数置为负无穷，我在这里简单用0代替：

0	a+2	0	0	0
b+1	0	b+3	0	b+5
0	c+2	0	c+4	0
0	0	d+3	0	d+5
0	e+2	0	e+4	0

这样mask一下，整个表格就会比较稀疏了。再将这个矩阵送入softmax，就可以得到注意力系数矩阵了。

到此，我们可以看另一个核心公式了：

这个公式就是原文里的公式(4)，因为完全一样，所以我直接用的截图。表示这层GAL关于节点i的输出特征，图中的表示节点i的邻接节点，表示注意力系数，直接查注意力系数矩阵就可得到。这里的依旧是激活函数的意思，代码中采用的是"elu"，不明白elu百度一下，一分钟就可理解。其实明白了的计算方式，这个公式很好理解吧。

看其在代码中的实现：(接着上面的，完整版请戳https://github.com/danielegrattarola/keras-gat)

            # Apply dropout to features and attention coefficients
            dropout_attn = Dropout(self.dropout_rate)(dense)  # (N x N)
            dropout_feat = Dropout(self.dropout_rate)(features)  # (N x F')

            # Linear combination with neighbors' features
            node_features = K.dot(dropout_attn, dropout_feat)  # (N x F')

            if self.use_bias:
                node_features = K.bias_add(node_features, self.biases[head])

            # Add output of attention head to final output
            outputs.append(node_features)

        # Aggregate the heads' output according to the reduction method
        if self.attn_heads_reduction == 'concat':
            output = K.concatenate(outputs)  # (N x KF')
        else:
            output = K.mean(K.stack(outputs), axis=0)  # N x F')

        output = self.activation(output)

代码中多加了一个dropout层，剩下没有解释的就是这个K了。

接下来是另一个trick，上文hold的attention heads我在这里详细讲解一下。

attention heads，就是文章中的K。

对于GAL而言，它可以完全仿照CNN的操作：CNN中对于每一层特征图的卷积核，其实可以有多个，而且每个卷积核相互独立，从而使得输出特征图具有更多的channel。

GAT也可以这样操作！先看图：

上图表示K=3时的情况，这个3在哪里呢？看波浪线，每个节点到节点1都有3条波浪线。这3条波浪线就代表3个独立的attention系数，，独立学习，并且有着独立的注意力系数矩阵。这也就解释了第一段代码中的那个for循环。

把公式(4)扩展到K大于1的情况:

这个公式代表中间层的输出形式，这里的双竖线‖依旧表示concatenate。而下面公式则代表输出层的输出形式：

输出层的用的时softmax。

以上，便是完整的清晰的GAT了。

总结

1， GAT是一种强大的空域图神经网络，是空域GNN的代表算法之一。

2，GAT的trick总结：1，使用了attention机制来描述邻接节点对于节点的重要性；2，采用邻接矩阵作为mask；3，引入了attention heads，即K，以扩展attention机制的channel;

3，一篇好文章是值得精读的。