算法-查找（红黑树）

查找

符号表

最主要的目的是将一个键和一个值联系起来。用例能够将一个键值对插入符号表并希望在之后能够从符号表的所有键值对中按照键直接找到对应的值，即以键值对为单元的数据结构。

无序链表顺序查找

性能：N方

有序数组二分查找

代码

public int rank(Key key){
    int lo = 0,hi = N-1;
    while(lo <= hi){
        int mid = lo + (hi - lo)/2;
        int cmp = key.compareTo(keys[mid]);
        if(cmp < 0) hi = mid - 1;
        else if(cmp > 0) lo = mid + 1;
        else return mid;
    }
    return -1;
}

性能：在N个键的有序数组中进行二分法查找最多需要(lgN+1)次比较(无论是否成功)

二叉查找树

定义：

一个二叉查找树(BST)是一颗二叉树，其中每个节点都含有一个Comparable的键(以及相关联的值)，且每个结点的键都大于其左子树中的任意节点的键而小于右子树的任意节点的键。

基本实现

get()查找,put()插入，
节点结构：键值，左连接，右链接，计数器

分析

使用二叉查找树的算法的运行时间取决于树的形状。在由N个随机键构成的二叉树中，查找命中平均所需的比较次数为~2lnN(约为1.39lgN)

有序性相关操作

1. 查找最大最小键
2. 向上向下取整（寻找大于给定值的最小键，小于给定值的最大键）
3. 选择（找到排名为k的键）
4. 排名（找到给定键的排名k）
5. 删除（删除最大最小键，删除任意键）
   删除任意键的算法：使用前继或后继节点替换空出的位置。
6. 范围查找
   中序遍历：
   按顺序打印：打印左子树->打印跟节点->打印右子树

private void print(Node x){
    if(x == null) return;
    print(x.left);
    System.out.println(x.key);
    print(x.right);
}

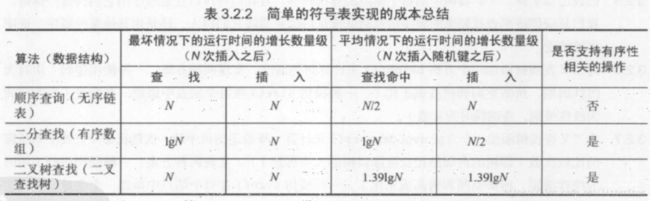
简单符号表成本总结

缺点

普通二叉查找树的高度跟键的插入顺序有关，对于足够大的N，这个值趋近于2.99lgN。但我们仍然无法保证二叉查找树的性能。而平衡二叉树就是解决了这一问题。

平衡查找树

2-3查找树

定义

一颗2-3查找树或是一颗空树，或由以下节点组成：

• 2-节点：一个键两链接
• 3-节点：两个键三链接

插入操作

1. 向2-结点插入新键：先进行一次未命中查找，将2-叶子结点替换成3-叶子结点。图3.3.3
   
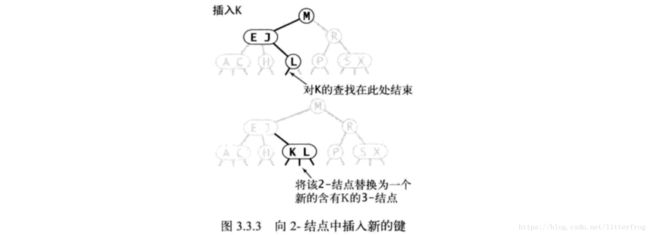
2. 向一棵只含有一个3-结点的树中插入新键：先临时将新键插入这个3-结点使之成为4-结点，再将4-结点的中间键上移，变换成3个2-结点，树的高度+1。图3.3.4
   
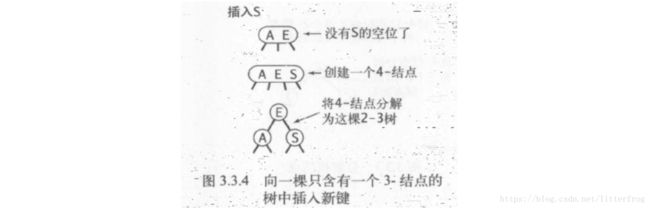
3. 向一个父节点为2-结点的3-结点中插入新键：跟2）中一样先生成一个临时的4-结点，将4-结点分解，但此时我们不会为中键创建一个新结点，而是将其移动至原来的父结点中。图3.3.5
   
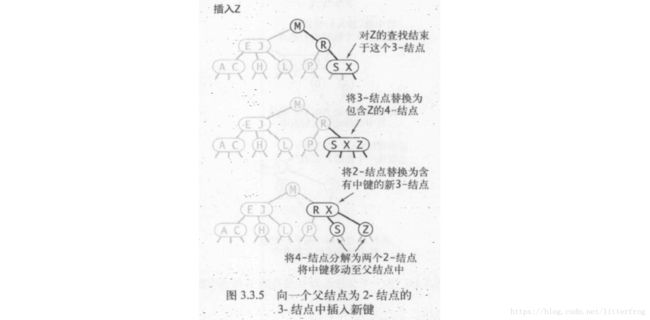
4. 向一个父节点为3-结点的3-结点中插入新键：递归重复4-结点的拆分。图3.3.6
   
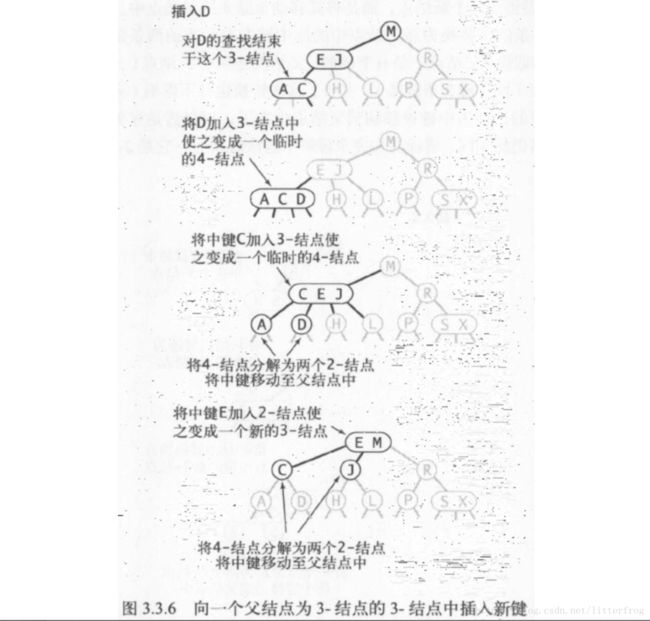
5. 2-3树的6种变换情况：图3.3.8
   

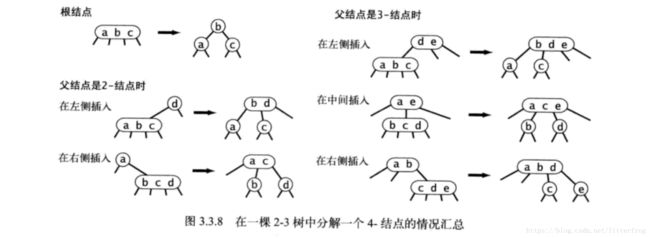
注意：以上变换都不会影响树的完美平衡性，因为除了根结点的4-分解情况之外，树的高度都不会增加，根结点的4-分解会使树的整体高度加1。

性能

在一棵大小为N的2-3树中，查找和插入操作访问的结点必然不超过lgN（N个结点的2-3树的高度在log(3)N=(lgN/lg3)和lgN之间。）
连续插入10个元素2-3树的生长情况：图3.3.10

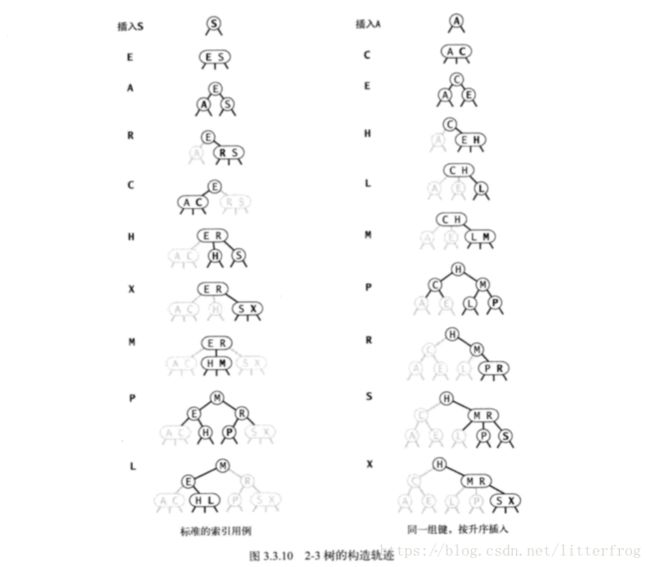
2-3树缺点

2-，3-结点的变换操作麻烦，需要处理的情况比较多，要维护两种不同的结点，难以把结点做简化的一致的抽象。
幸运的是你将看到，我们只需要一点点代价就能用一种统一的方式完成所有变换。

红黑二叉树

旋转时，把红节点的父链接看成一条红线，红线上的内侧子结点（即红色左链接的右子结点或红色右链接的左子结点）可以在红线上沿着重力的方向自由滑动。

红黑树的由来：替换3-结点

红黑二叉查找树背后的基本思想是用标准的二叉查找树（完全由2-结点构成）和一些额外的信息（替换3-结点）来表示2-3树。我们将树中的链接分为两种类型：红链接将两个2-结点连接起来构成一个3-结点，黑链接则是2-3树中的普通链接。确切地说，我们将3-结点表示为由一条左斜的红色链接（两个2-结点中小的是大的的左子结点）相连的两个2-结点，如下图3.3.12。我们将用这种方式表示2-3树的二叉查找树成为红黑二叉查找树。

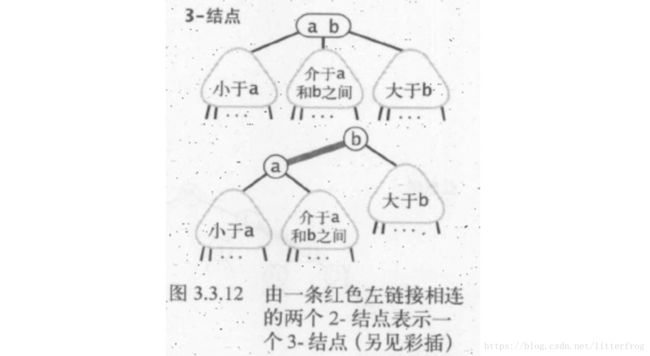
等价定义

红黑树的另一种定义是含有红黑链接并满足下列条件的二叉查找树：

1. 红链接均为左链接
2. 没有任何一个结点同时和两条红链接相连
3. 该树是完美黑平衡的，即任意空链接到根结点的路径上的黑链接数量相同。

与2-3树对应关系

如果将一棵红黑树中的红链接画平，那么所有的空链接到根结点的距离都将是相同的。如果我们将由红链接相连的节点合并，得到的就是一棵2-3树。图3.3.13

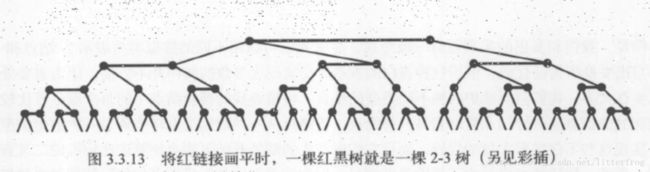
颜色表示

方便起见，因为每个结点都只会有一条指向自己的链接（从它的父节点指向它），我们将链接的颜色保存在表示结点的Node数据类型的red成员中。具体见代码

public class Node,Value>{
    Key key;
    Value value;
    Node left,right;
    int N;
    boolean red;

    public Node(Key key,Value value,int N,boolean red){
        this.key = key;
        this.value = value;
        this.N = N;
        this.red = red;
    }

    private boolean isRed(Node x){
        if(x == null){
            return false;
        }
        return x.red;
    }
}

旋转

修复红黑树，使得红黑树中不存在红色右链接或两条连续的红链接。

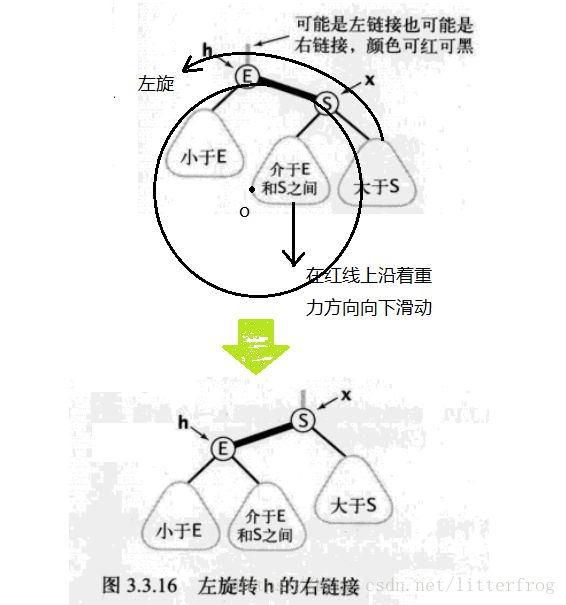
左旋

将红色的右链接转化为红色的左链接，如图3.3.16

代码

Node rotateLeft(Node h){
    Node x = h.right;
    h.right = x.left;
    x.left = h;
    x.color = h.color;
    h.color = true;
    x.N = h.N;
    h.N = 1 + size(h.left) + size(h.right);
    return x;
}

右旋

将红色的左链接转化为红色的右链接，代码与左旋完全相同，只要将left换成right即可。如图3.3.17

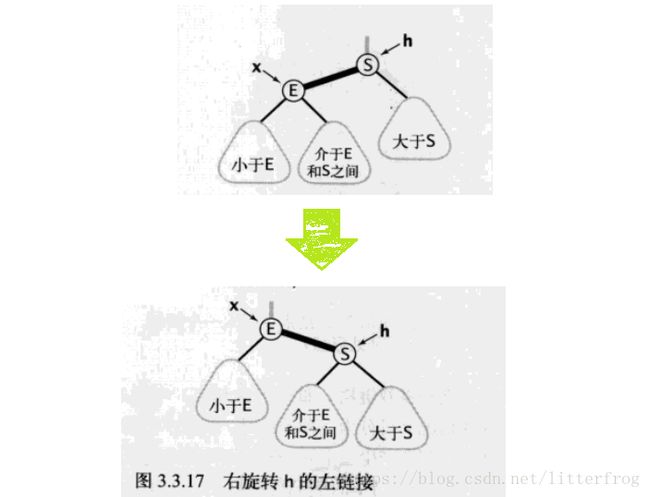
代码

Node rotateRight(Node h){
    Node x = h.left;
    h.left = x.right;
    x.right = h;
    x.color = h.color;
    h.color = true;
    x.N = h.N;
    h.N = 1 + size(h.left) + size(h.right);
    return x;
}

插入结点

在插入新的键时，我们可以使用旋转操作帮助我们保证2-3树和红黑树之间的一一对应关系，因为旋转操作可以保持红黑树的两个重要性质：有序性和完美平衡性。也就是说，我们在红黑树中进行旋转时无需为树的有序性或者完美平衡性担心。下面我们来看看应该如何使用旋转操作来保持红黑树的另外两个重要性质：不存在两条连续的红链接和不存在红色的右链接。我们先用一些简单的情况热热身。

1.向树底部的2-结点插入新键

一棵只含有一个键的红黑树只含有一个2-结点。插入另一个键之后，我们马上就需要将他们旋转。如果新键小于老键，我们只需要新增一个红色的节点即可，新的红黑树和单个3-结点完全等价。如果新键大于老键，那么新增的红色节点将会产生一条红色的右链接。我们需要使用parent = rotateLeft(parent);来将其旋转为红色左链接并修正根结点的链接，插入才算完成。两种情况均把一个2-结点转换为一个3-结点，树的黑链接高度不变，如图3.3.18和3.3.19

2.向一棵双键树（即一个3-结点）中插入新键

这种情况又可分为三种子情况：新键小于树中的两个键，在两者之间，或是大于树中的两个键。每种情况中都会产生一个同时链接到两条红链接的结点，而我们的目标就是修正这一点。

1. 三者中最简单的情况是新键大于原树中的两个键，因此它被链接到3-结点的右链接。此时树是平衡的，根结点为中间大小的键，它有两条红链接分别和较小和较大的结点相连。如果我们将两条链接的颜色都由红变黑，那么我们就得到了一棵由三个结点组成，高为2的平衡树。它正好能够对应一棵2-3树，如图3.3.20（左）。其他两种情况最终也会转化为这两种情况。
2. 如果新键小于原书中的两个键，它会被链接到最左边的空链接，这样就产生了两条连续的红链接，如果3.3.20（中）。此时我们只需要将上层的红链接右旋转即可得到第一种情况。
3. 如果新键介于原书中的两个键之间，这又会产生两条连续的红链接，一条红色左链接接一条红色右链接，如果3.3.20（右）。此时我们只需要将下层的红链接左旋即可看得到第二种情况。
   

3.颜色转换

如图3.3.21，我们专门用一个方法flipColors()来转换一个结点的两个红色字结点的颜色。除了将子结点的颜色由红变黑之外，我们同时还要将父节点的颜色由黑变红。这项操作最重要的性质在于它和旋转操作一样是局部变换，不会影响整棵树的黑色平衡性。根据这一点，我们马上就能在下面完整实现红黑树。

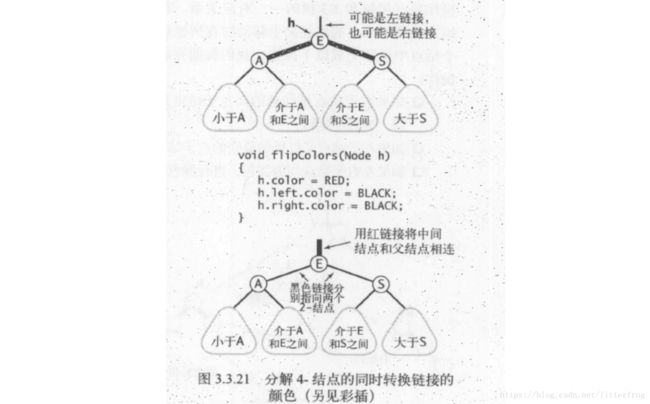
4.根结点总是黑色

颜色转换会使根结点变为红色，我们在每次插入操作后都会将根结点设为黑色。

5.向树底部的3-结点插入新键

现在假设我们需要在树的底部的一个3-结点下加入一个新结点。前面讨论过的三种情况都会出现，如图3.3.22所示。颜色转换会使指向中结点的链接变红，相当于将它送入了父结点。这意味着在父结点中继续插入一个新键，我们也会继续用相同的办法解决这个问题。

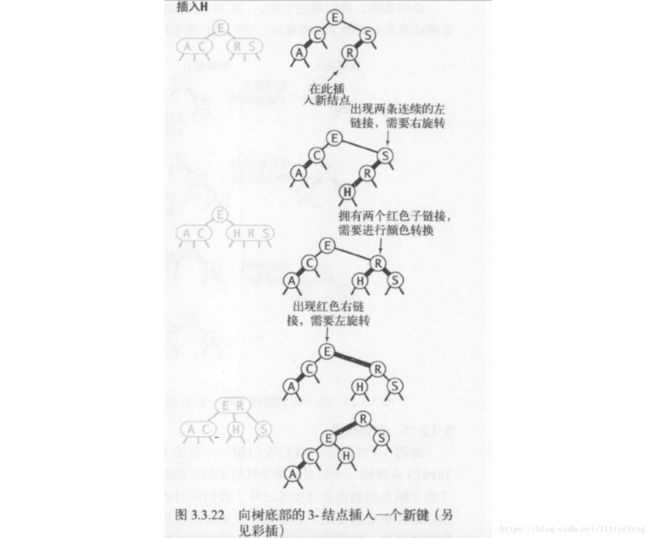
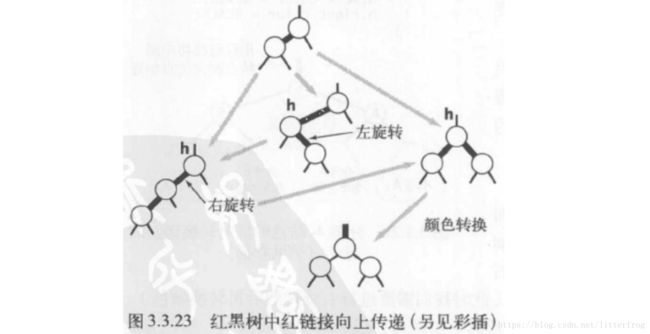
6.将红链接在树中向上传递

2-3树中的插入算法需要我们分解3-结点，将中间键插入父结点，如此这般知道遇到一个2-结点或是根结点。总之，只要谨慎地使用左旋，右旋，颜色转换这三种简单的操作，我们就能保证插入操作后红黑树和2-3树的一一对应关系。在沿着插入点到根结点的路径向上移动时在所经过的每个结点中顺序完成以下操作，我们就能完成插入操作：

1. 如果右子结点是红色的而左子结点是黑色的，进行左旋转
2. 如果左子结点是红色的且她的左子结点也是红色的，进行右旋
3. 如果左右子结点均为红色，进行颜色转换。
   如图3.3.23
   

实现

从上到下查找，由下至上进行平衡变换，如下代码

public class RedBlackBST{
    private Node root;
    private boolean isRed(Node h);
    private Node rotateLeft(Node h);
    private Node rotateRight(Node h);
    private void flipColors(Node h);

    private int size(Node node);

    public void put(Node freshNode){
        //查找key，找到则更新其值，否则为它新键一个结点
        root = put(root,freshNode);
        root.red = false;
    }
    private Node put(Node h,Node freshNode){
        if(h == null){//标准插入操作，和父结点用红链接相连
            return new Node(freshNode.key,freshNode.value,1,true);
        }
        int cmp = freshNode.key.compareTo(h.key);
        if(cmp < 0) h.left = put(h.left,freshNode);
        else if(cmp > 0) h.right = put(h.right,freshNode);
        else h.value = freshNode.value;
        
        if(isRed(h.right) && !isRed(h.left)) h = rotateLeft(h);
        if(isRed(h.left) && isRed(h.left.left)) h = rotateRight(h);
        if(isRed(h.left) && isRed(h.right)) flipColors(h);
        
        h.N = size(h.left) + size(h.right) + 1;
        return h;
    }
}

删除操作

要描述删除算法，首先要回到2-3树。和插入操作一样，我们也可以定义一系列局部变换来在删除一个结点的同时保持树的完美平衡性。这个过程比插入一个结点更加复杂，因为我们不仅要在（为了删除一个结点而）构造临时4-结点时沿着查找路径向下进行变换，还要在分解遗留的4-结点时沿着查找路径向上进行变换（同插入操作）。

1.自顶向下的2-3-4树

作为第一轮热身，我们先学习一个沿着查找路径既能向上也能向下进行变换的稍简单的算法：2-3-4树的插入算法，2-3-4树中允许存在我们以前见过的4-结点。它的插入算法沿着查找路径向下进行变换是为了保证当前结点不是4-结点（这样树底才有空间来插入新的键），沿着查找路径向上进行变换是为了将之前创建的4-结点配平，如图3.3.25所示。

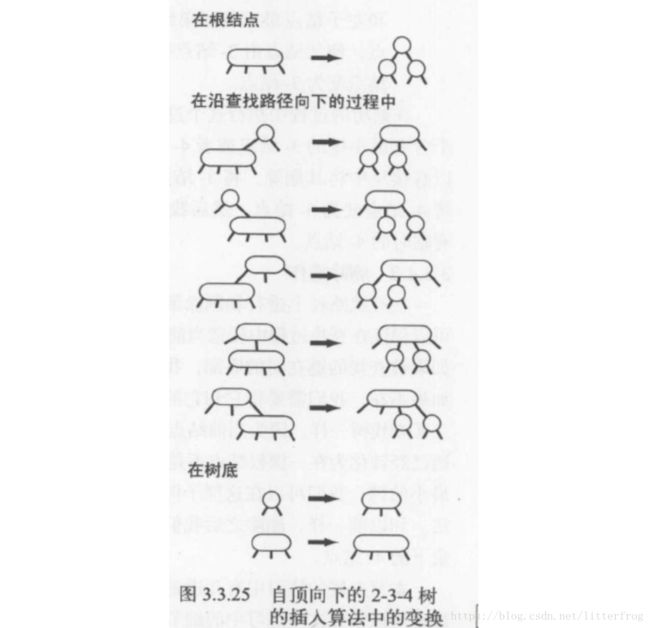
向下的变换和我们在2-3树中分解4-结点所进行的变换完全相同。如果根结点是4-结点，我们就将它分解成三个2-结点，使得树高加1。在向下查找的过程中，如果遇到一个父结点为2-结点的4-结点，我们将4-结点分解为两个2-结点并将中间键传递给他的父结点，使得父结点变为一个3-结点；如果遇到一个父结点为3-结点的4-结点，我们将4-结点分解为两个2-结点并将中间键传递给它的父结点，使得父结点变为一个4-结点；我们不必担心会遇到父结点为4-结点的4-结点，因为插入算法本身就保证了这种情况不会出现。到达树的底部之后，我们也只会遇到2-结点或者3-结点，所以我们可以插入新的键。要用红黑树实现这个算法，我们需要：

1. 将4-结点表示为由三个2-结点组成的一颗平衡的子树，根结点和两个子结点都用红链接相连；
2. 在向下的过程中分解所有4-结点并进行颜色转换；
3. 和插入操作一样，在向上的过程中用旋转将4-结点配平。（因为4-结点可以存在，所以可以允许一个结点同时链接两条红链接）。
   令人惊讶的是，你只需要移动上面算法的put()方法中的一行代码就能实现2-3-4树中的插入操作：将colorFlip()语句（及其if语句）移动到递归调用之前（null测试和比较操作之间）。在多个进程可以同时访问同一棵树的应用中这个算法优于2-3树。

2.删除最小键

在第二轮热身中我们要学习2-3树中删除最小键的操作。我们注意到从树底部的3-结点中删除键是很简单的，但2-结点则不然。从2-结点中删除一个键会留下一个空结点，一般我们会将它替换为一个空链接，但这样会破坏树的完美平衡。所以我们需要这样做：为了保证我们不会删除一个2-结点，我们沿着左链接向下进行变换，确保当前结点不是2-结点（可能是3-结点，也可能是临时的4-结点）。首先根结点可能有两种情况。如果根是2-结点且它的两个子结点都是2-结点，我们可以直接将这三个结点变为一个4-结点；否则我们需要保证根结点的左子结点不是2-结点，如有必要可以从它右侧的兄弟结点“借”一个键来。以上情况如图3.3.26所示。

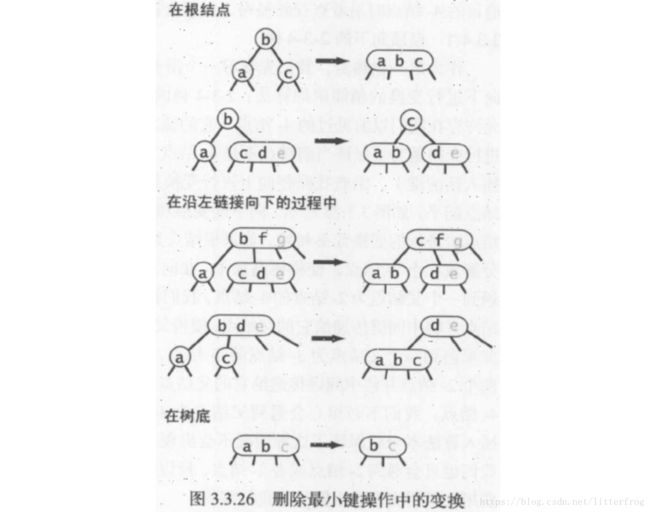
在沿着左链接向下的过程中，保证以下情况之一成立：

1. 如果当前结点的左子结点不是2-结点，完成；
2. 如果当前结点的左子结点是2-结点而它的亲兄弟结点不是2-结点，将左子结点的兄弟结点中的一个键移动到左子结点中；
3. 如果当前结点的左子结点和它的亲兄弟结点都是2-结点，将左子结点，父结点中的最小键和左子结点最近的兄弟结点合并为一个4-结点，使父结点由3-结点变为2-结点或由4-结点变为3-结点。

3.删除操作

在查找路径上进行和删除最小键相同的变换同样可以保证在查找过程中任意当前结点均不是2-结点。如果被查找的键在树的底部，我们可以直接删除它。如果不在，我们需要将它和它的后继结点交换，就和二叉树一样。因为当前结点必然不是2-结点，问题已经转化为在一颗根结点不是2-结点子树中删除最小键，我们可以在这个子树中使用前问所述的算法。和以前一样，删除之后我们需要向上回溯并分解余下的4-结点。
红黑树的性质
重要结论：所有基于红黑树的符号表实现都能保证操作的运行时间为对数级别。
一颗大小为N的红黑树的高度不会超过2lgN。这个上界是比较保守的，实际上，一颗大小为N的红黑树中，根结点到任意结点的平均路径长度为～1.001lgN。
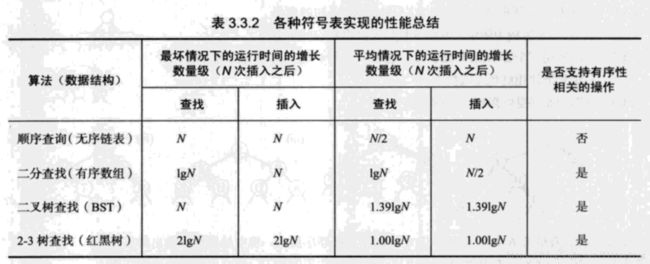
各种符号表的性能总结