webrtc VAD 算法

webrtc VAD 算法

简介

本文的目地是为了尽可能少的使用公式将webrtc的VAD算法讲清楚，为此忽略算法的证明以及算法的严谨性，力求通俗易懂，多讲实例。
因为webrtc的VAD算法主要使用了GMM高斯混合模型，所以重点在于理解GMM，要想理解GMM，又离不开K-means聚类和EM估计，下面从K-means开始说起。

一，K-means 聚类

K-means 属于传统机器学习中的无监督学习，体现了聚类思想，他可以对没有标签的数据进行分类，聚类过程主要分两步：

• K:描述了簇的数量，也就是应当聚合成的几何数；
• means:均值求解，确定已分类数据的聚类中心(Cluster Centroid)位置；

具体实现步骤：
(1)根据设定的聚类数 K ，随机地选择 K 个聚类中心(Cluster Centroid)，这里要注意聚类中心(Cluster Centroid)的初始值(就是图中X的位置)会影响最终的分类结果

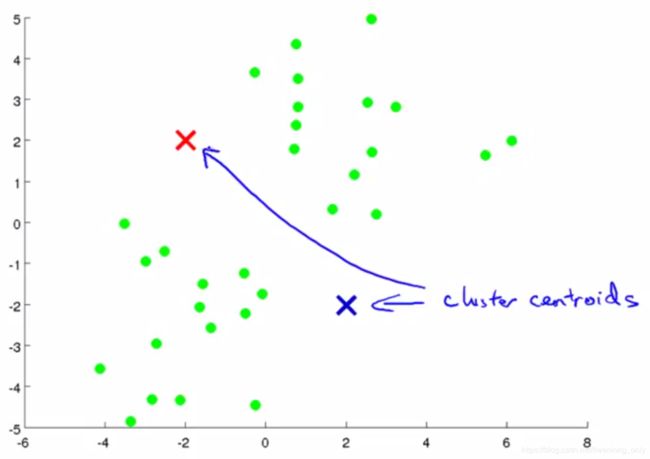
(2)评估各个样本到聚类中心的距离，如果样本距离第 i 个聚类中心更近，则认为其属于第 i 簇,
$$欧式距离：d=\sqrt{(x_1-x_2{)}^2+(y_1-y_2{)}^2}$$
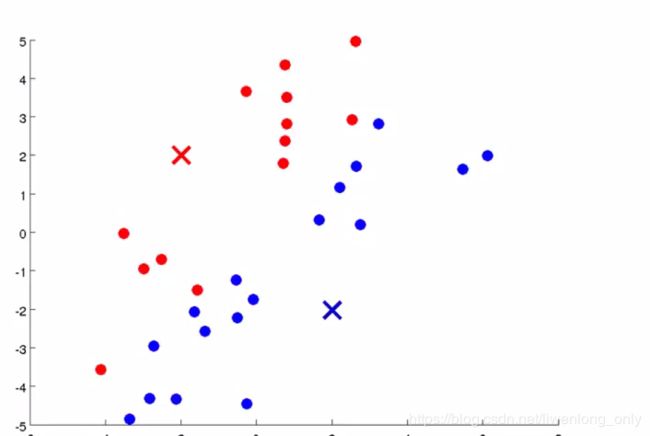
(3)计算每个簇中样本的平均（Mean）位置，将聚类中心移动至该位置，实际就是求每个簇的数据在x轴和y轴上的平均值
$$其中\mu i是簇K_i的均值向量，有时也称为质心，表达式为：u_i=\frac{1}{|K_i|}\sum _{x\in K_i}x$$

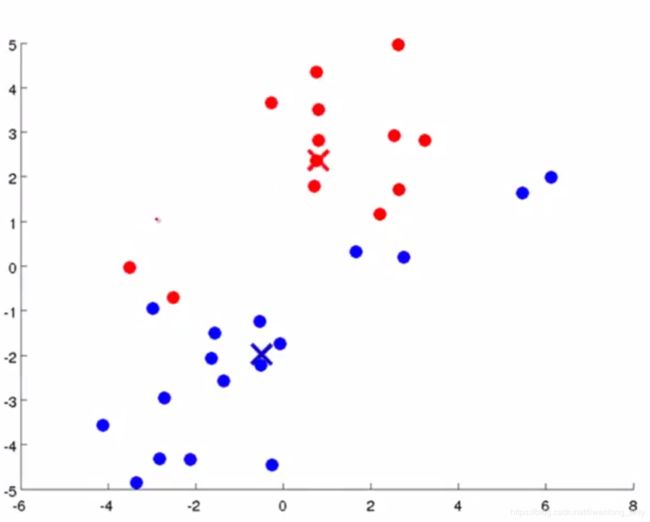
重复以上(2),(3)步骤直至各个聚类中心的位置不再发生改变(这个过程一定会收敛，证明这里就不介绍了，主要理解聚类的思想)

K-means 演示实例（需要）

二，EM估计

1，似然函数和极大似然估计

硬币	结果	统计
1	正正反正反	3正-2反

如上图所示，如果我们知道这个硬币正面朝上的概率是0.5，那么抛5次有3次正面朝上的概率是0.5x0.5x0.5=0.125（这个是概率），如果我们不知道这个硬币正面朝上的概率，那么抛5次有3次正面朝上，现在求这个硬币正面朝上的概率是3/5=0.6(这个就是似然)，似然和概率都是大概的意思，但是在统计学上是不同的。
现在考虑一个问题，上一步求出的硬币正面朝上的概率为什么是3/5=0.6，为什么正面朝上的次数除以总次数就是硬币正面朝上的概率，其实这个就是用极大似然估计推导出来的，下面我们就看一下这个3/5=0.6的由来。

• 已知硬币连续抛5次，3正2反，求硬币正面朝上的概率，假设正面朝上的概率为$\theta$,似然函数为：
  $$L(\theta )=L(x_1,...x_n;\theta )=\prod _{i=1}^{n}p(x_i;\theta ),\theta \in \Theta$$
  在我们这个例子中似然函数为：
  $$L(\theta )=\prod _{i=1}^3\theta \prod _{i=1}^2(1-\theta )$$

• 极大似然估计就是求似然函数$L(\theta )$最大时，$\theta$的取值，这就转化成一个纯数学问题，求导，令导数等于0，就可以得到$\theta$的值，为了便于分析，还可以定义对数似然函数，将其变成连加的：
  $$H(\theta )=lnL(\theta )=ln\prod _{i=1}^{n}p(x_i;\theta )=\sum _{i=1}^{n}lnp(x_i;\theta ),\theta \in \Theta$$
  在我们这个例子中对数似然函数为：
  $$H(\theta )=lnL(\theta )=ln\prod _{i=1}^3\theta +ln\prod _{i=1}^2(1-\theta )=\sum _{i=1}^{3}ln\theta +\sum _{i=1}^{2}ln(1-\theta )$$
  我们对$H(\theta )$求导，并令导数等于0，求解$\theta$:
  $$H(\theta )=\sum _{i=1}^{3}ln\theta +\sum _{i=1}^{2}ln(1-\theta )$$
  $$H(\theta )=3ln\theta +2ln(1-\theta )$$
  $${H(\theta )}^{\prime }=\frac{3}{\theta }+\frac{2}{1-\theta }\times -1$$
  $${H(\theta )}^{\prime }=\frac{3(1-\theta )}{\theta (1-\theta )}+\frac{-2\theta }{(1-\theta )\theta }$$
  $${H(\theta )}^{\prime }=\frac{3-5\theta }{(1-\theta )\theta }$$
  令${H(\theta )}^{\prime }=0$，得：$\frac{3-5\theta }{(1-\theta )\theta }=0$，所以$3-5\theta =0$, 最终$\theta =3/5=0.6$。

• 这就是极大似然估计，总结一下计算步骤：
  （1）写出似然函数；
  （2）对似然函数取对数，并整理；
  （3）求导数，令导数为0，得到似然方程；
  （4）解似然方程，得到的参数即为所求；

2，EM估计

• 通过一个简单的例子来了解EM算法，假设现在有两枚硬币1和2，,随机抛掷后正面朝上概率分别为P1，P2。为了估计这两个概率，做实验，每次取一枚硬币，连掷5下，记录下结果，如下：

硬币	结果	统计
1	正正反正反	3正-2反
2	正反反正反	2正-3反
1	正反正正反	3正-2反

• 根据极大似然估计，我们很容易计算出p1和p2
  p1=(3+3)/10 = 0.6
  p2=2/5 = 0.4
• 现在加大难度，还是求两枚硬币正面朝上的概率p1,p2，如下图所示：

硬币	结果	统计
未知	正正反正反	3正-2反
未知	正反反正反	2正-3反
未知	正反正正反	3正-2反

• 现在引入了未知变量，如何求p1,p2呢？假设未知变量是k，它是个3维向量[k1,k2,k3]，要求k，我们需要知道p1，p2，要求p1,p2，又要知道k，怎么办呢？要解决这个问题就要用到EM估计。

• 首先我们假设一个p1,p2的值，然后用这个假设的值去求k，有了k之后，我们在利用极大似然估计去求p1和p2，然后看一下求出的p1和p2，与我们刚才假设的值是否相等，如果不相等，就用这个p1和p2去求k，在用k，求出一个新的p1和p2，一直迭代下去，直到求出的p1和p2与上一次求出的p1和p2相等，这个时候的p1和p2就是我们要求的答案了，这个过程是收敛的，证明过程请参考其他资料，下面我们针对这个例子来一步一步走一遍。

• 首先我们假设p1=0.7，p2=0.3，计算第一轮实验，硬币是第一枚和是第二枚硬币的可能性

• 第一步，求出未知变量k：
  p(硬1)=0.7x0.7x0.7x(1-0.7)x(1-0.7)=0.03087
  p(硬2)=0.3x0.3x0.3x(1-0.3)x(1-0.3)=0.01323
  因为p(硬1)>p(硬2)，所以第一轮最有可能用的是第一枚硬币，依次求出剩下的两轮，如下表：

轮数	是硬币1的概率	是硬币2的概率
1	0.03087	0.01323
2	0.01323	0.03087
3	0.03087	0.01323

所以k=[硬币1，硬币2，硬币3];

• 第二步，根据求出的k=[硬币1，硬币2，硬币3]，利用极大似然估计求出p1和p2
  p1=(3+3)/10 = 0.6
  p2=2/5 = 0.4
• 第三步，根据第二步求出的p1和p2，与第一步使用的p1和p2做比较，如果相等就停止，不相等就重复第一步和第二步，直到相等为止，又是一个迭代的过程，这个算法也一定会收敛，证明过程请参考其他资料

三，GMM 高斯混合模型

1，高斯分布和极大似然估计求解

• 正态分布（Normal distribution），也称“常态分布”，又名高斯分布（Gaussian distribution），最早由A.棣莫弗在求二项分布的渐近公式中得到。C.F.高斯在研究测量误差时从另一个角度导出了它。P.S.拉普拉斯和高斯研究了它的性质。是一个在数学、物理及工程等领域都非常重要的概率分布，在统计学的许多方面有着重大的影响力。

• 一维正态分布，若随机变量X服从一个数学期望为μ、标准方差为σ2的高斯分布，记为：
  $$X\sim N(u,{\sigma }^2)$$
  则其概率密度函数为:
  $$f(x)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{(x-u{)}^2}{2{\sigma }^2}}$$
  图像如下：
  

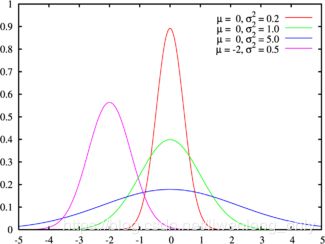
• 有一点要注意某一点x的值f(x),并不是x点对应的概率值，他代表的是概率累积函数在这点的导数，也就是梯度，但是他其实可以近似的表示某个点落在高斯分布$x\in [x,x+0.001]$所围城图形上的概率。

• 现在我们看一下高斯分布公式中的两个未知参数是怎么求解的，有没有感觉和前面求解硬币正面朝上的概率很熟悉，没错，它也是用极大似然估计求解的，只不过它有两个参数$u,{\sigma }^2$，求解的套路是一样的，先求出高斯分布的对数似然函数，然后求导，令导数等于0，求解参数，这里要注意，由于有两个未知的参数，所以需要求偏导，令导数等于0，求解过程就不写了，直接列出最后的结果：
  $$u=\frac{1}{n}\sum _{i=1}^n{x}_i$$

$${\sigma }^2=\frac{1}{n}\sum _{i=1}^n(x_i-u{)}^2$$
2，GMM求解

• 这里引用李航老师《统计学习方法》上的定义，如下：
  
• GMM其实就是把多个高斯分布乘以一个系数$a_k$,然后在累加起来，有没有发现$a_k$和我们前面讲的EM估计中的向量k=[硬币1，硬币2，硬币3]很像，没有错它们都称为隐含变量，下面我们就用包含两个高斯分布的GMM来举例
• 假设我们有10个身高数据$[166_{女}，178_{男}，155_{女}，175_{男}，160_{女}，180_{男}，163_{女}，188_{男}，170_{女}，170_{男}]$
  男生和女生的身高都分别符合一个高斯分布，根据前面的极大似然估计我们可以求出：
  $$u_{男}=\frac{1}{n}\sum _{i=1}^n{x}_i=\frac{1}{5}(178+175+180+188+170)=178.2$$

$${\sigma }_{男}^2=\frac{1}{n}\sum _{i=1}^n(x_i-u{)}^2=\frac{1}{5}((178-178.5{)}^2+(175-178.5{)}^2+(180-178.5{)}^2+(188-178.5{)}^2+(170-178.5{)}^2)=44.2$$

$$u_{女}=\frac{1}{n}\sum _{i=1}^n{x}_i=\frac{1}{5}(166+155+160+163+170)=162.8$$

$${\sigma }_{女}^2=\frac{1}{n}\sum _{i=1}^n(x_i-u{)}^2=\frac{1}{5}((166-162.8{)}^2+(155-162.8{)}^2+(160-162.8{)}^2+(163-162.8{)}^2+(170-162.8{)}^2)=32.7$$

• 假设我们获得的10个身高数据是$[166_{未知}，178_{未知}，155_{未知}，175_{未知}，160_{未知}，180_{未知}，163_{未知}，188_{未知}，170_{未知}，170_{未知}]$，我们知道他们是属于两个高斯分布，我要如何求出这个高斯分布呢？，有没有一种熟悉的味道，和上面讲解的EM估计非常类似，其实他们的思想是一样的，我下面就一步一步计算一遍
• 首先假设$u_{男}$=178，${\sigma }_{男}^2$=44，$u_{女}$=162，${\sigma }_{女}^2$=32，
• 第一步，求第一个数据166的可能性为：
  $$f(166{)}_{男}=\frac{1}{\sqrt{44}\sqrt{2\pi }}{e}^{-\frac{(166-178{)}^2}{2\times 44}}=0.0735688$$

$$f(166{)}_{女}=\frac{1}{\sqrt{32}\sqrt{2\pi }}{e}^{-\frac{(166-162{)}^2}{2\times 32}}=0.345092$$
因为$f(166{)}_{男}<f(166{)}_{女}$,所以166这个数据属于女生的高斯分布的可能性大，下面我们计算剩余的数据；

身高	男生高斯分布的可能性	女生高斯分布的可能性
166	0.0735688	0.345092
178	0.377883	0.00811579
155	0.000926094	0.206064
175	0.341146	0.0316009
160	0.00951402	0.41626
180	0.361091	0.00280474
163	0.0293052	0.436237
188	0.121294	0.000011
170	0.182602	0.16301
170	0.182602	0.16301

我们根据可能性的大小，确定数据的属于那个分布，$166_{女}，178_{男}，155_{女}，175_{男}，160_{女}，180_{男}，163_{女}，188_{男}，170_{男}，170_{男}$

• 第二步，根据极大似然估计来计算两个高斯分布的$u,{\sigma }^2$
• 第三步，判断新计算的$u,{\sigma }^2$与上一次的$u,{\sigma }^2$是否相等，如果不相等重复第一步和第二步；
• 这里有个问题，我们知道GMM中有个权重系数$a_k$可是我们刚才并没有出现这个$a_k$，其实是为了方便直接使用男或女表示了，如果使用$a_k$表示，则数据$166_{女}$，就表示为$166_{[0,1]}$，GMM是多个高斯分布乘以系数$a_k$，然后相加得到的，所以：
  $$166_{女}=166_{[0,1]}=0\times 男生高斯分布+1\times 女生高斯分布=女生高斯分布$$

四，webrtc 中的 VAD 实现

1，VAD激进模式设置

• 共四种模式，用数字0~3来区分，激进程度与数值大小正相关。
  0: Normal，1：low Bitrate， 2：Aggressive；3：Very Aggressive

2，帧长设置

• 共有三种帧长可以用到，分别是80/10ms，160/20ms，240/30ms，实际上目前只支持10ms的帧长。
• 其它采样率的48k，32k，24k，16k会重采样到8k来计算VAD。之所以选择上述三种帧长度，是因为语音信号是短时平稳信号，其在10ms-30ms之间可看成平稳信号，高斯马尔科夫等信号处理方法基于的前提是信号是平稳的，在10ms~30ms，平稳信号处理方法是可以使用的。

3，高斯模型中特征向量选取

• 在WebRTC的VAD算法中用到了聚类的思想，只有两个类，一个类是语音，一个类是噪声，对每帧信号都求其是语音和噪声的概率，根据概率进行聚类，当然为了避免一帧带来的误差也有一个统计量判决在算法里，那么问题来了，选择什么样的特征作为高斯分布的输入呢?这关系到聚类结果的准确性，也即VAD性能，毋庸置疑，既然VAD目的是区分噪声和语音，那么噪声信号和语音信号这两种信号它们的什么特征相差最大呢?选择特征相差比较大自然能得到比较好的区分度。

• 众所周知，信号的处理分类主要有时域，频域和空域，从空域上看，webRTC的VAD是基于单麦克的，噪声和语音没有空间区分度的概念，在多麦克风场景，确实基于多麦克风的VAD算法，从时域上看，而者都是时变信号，且短时信号变化率比较小，所以推算来推算去只有频域的区分度可能是比较好的。

• 汽车噪声频谱
  

• 粉红噪声频谱
  

• 白噪声频谱
  

• 语音声谱
  

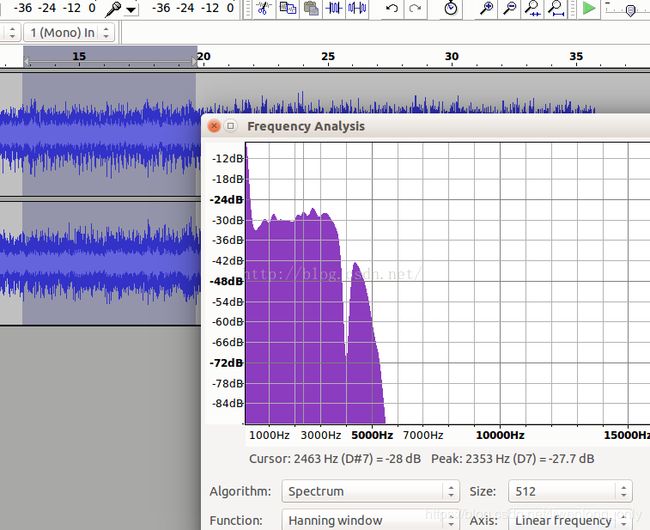
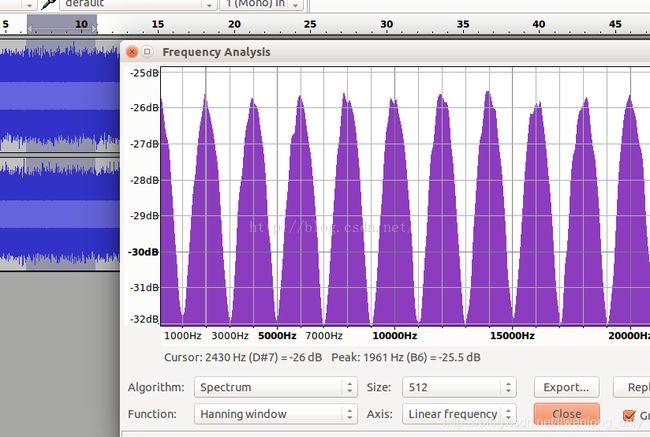
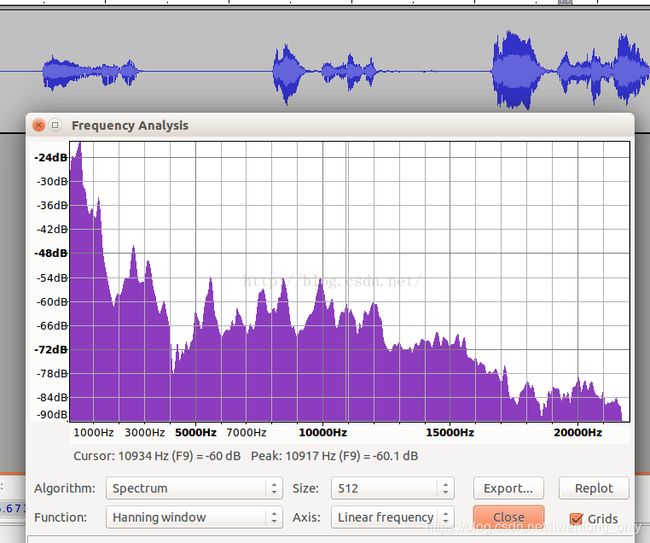
• 从以上四个图中，可以看到从频谱来看噪声和语音，它们的频谱差异还是比较大，且以一个个波峰和波谷的形式呈现。

• WebRTC正式基于这一假设，将频谱分成了6个子带。它们是：80Hz_{250Hz，250Hz}500Hz,500Hz_1K,1K2K,2K_3K,3K4K。分别对应于feature[0],feature[1],feature[2],…,feature[5]。

• 可以看到以1KHz为分界，向下500HZ，250Hz以及170HZ三个段，向上也有三个段，每个段是1KHz，这一频段涵盖了语音中绝大部分的信号能量，且能量越大的子带的区分度越细致。

• 我国交流电标准是220V~50Hz，电源50Hz的干扰会混入麦克风采集到的数据中且物理震动也会带来影响，所以取了80Hz以上的信号。

• 这个模型和我们上面讲个的身高的例子，原理是一样的，只是这个例子的输入不是身高的值，而是子带能量，这个GMM包含两个高斯分布，一个是语音的高斯分布，一个是噪音的高斯分布

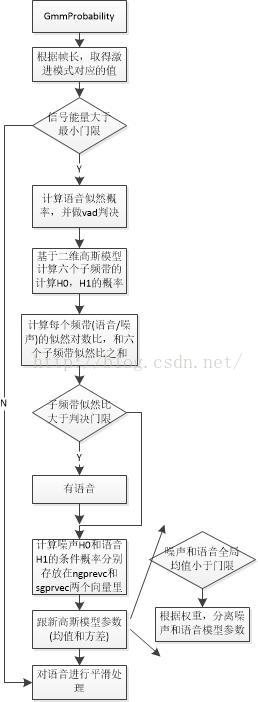
3，计算流程

• 高斯模型有两个参数H0和H1，它们分表示的是噪声和语音，判决测试使用LRT（likelihood ratio test，似然比检测）。分为全局和局部两种情况
  

4，参数更新

• 噪声均值更新，参数更新就是使用极大似然估计根据已经分类完的数据去重新计算均值$u$和方差${\sigma }^2$，WebRtcVad_FindMinimum函数对每个特征，求出100个帧里头的前16个最小值。每个最小值都对应一个age，最大不超过100，超过100则失效，用这个最小值来跟新噪声，这里要注意为什么要使用部分数据而不是全部的数据去更新参数呢，这个和随机梯度下降法是一个道理，因为数据太多了，计算量会很大，10ms 音频就有6个样本，如果是一个小时呢？

• 更新噪声均值，语音均值，噪声方差，语音方差，自适应也就体现在这里

五，参考资料：

https://blog.csdn.net/shichaog/article/details/52399354/
https://www.jianshu.com/p/1121509ac1dc
https://blog.csdn.net/zouxy09/article/details/8537620