人工智能——凸函数及其相关问题
人工智能——凸函数及其相关问题 目录
- 一、凸集
- 1. 定义
- 2. 性质
- 凸函数
- 1. 定义
- 2. 几何性质
- 凸规划
- 1. 定义
- 2. 性质
- 相关问题
- 问题一：计算几何是什么？
- 问题二：计算几何理论中过两点的一条直线的表达式，是如何描述的？
- 问题三：凸集是什么？ 直线是凸集吗？是仿射集吗？
- 问题四：三维空间中的一个平面，如何表达？
- 问题五：更高维度的“超平面”，如何表达？
- 问题六：什么是“凸函数”定义？如何判别一个函数是凸函数？（见文章开头）
- 问题七：什么是“凸规划”？如何判别一个规划问题是凸规划问题。举例说明？（见文章开头）
一、凸集
1. 定义
设集合 D ⊂ R n D\subset R^n D⊂Rn ，若对于任意两点 x , y ∈ D x,y\in D x,y∈D ，及实数 a ( 0 ≤ a ≤ 1 ) a(0\leq a \leq1) a(0≤a≤1)，都有：
a x + ( 1 − a ) y ∈ D , ax+(1-a)y\in D, ax+(1−a)y∈D,
则称集合 D D D为凸集
常见凸集：单点集 { x } \{x\} {x}，空集 ∅ \emptyset ∅ ，整个欧式空间 R n R^n Rn。
2. 性质
（1）任意多个凸集的交集为凸集
（2）设 D D D是凸集， β \beta β是一实数，则下面的集合是凸集： β D = { y ∣ y = β x , x ∈ D } \beta D=\{y|y=\beta x,x\in D\} βD={y∣y=βx,x∈D}
（3）设 D 1 D_1 D1和 D 2 D_2 D2是集合 R n R^n Rn上的凸集，则：
a. D 1 + D 2 = { x 1 + x 2 ∣ x 1 ∈ D , x 2 ∈ D } D_1+D_2=\{x_1+x_2|x_1\in D,x_2\in D\} D1+D2={x1+x2∣x1∈D,x2∈D}是凸集。
b. D 1 − D 2 = { x 1 − x 2 ∣ x 1 ∈ D , x 2 ∈ D } D_1-D_2=\{x_1-x_2|x_1\in D,x_2\in D\} D1−D2={x1−x2∣x1∈D,x2∈D}
（4）S是凸集当且仅当S中任意有限个点的凸组合任然在S中。
凸函数
1. 定义
设 D ⊆ R n D\subseteq R^n D⊆Rn 是非空集， f ( x ) : S → R f(x):S\rightarrow R f(x):S→R，若对任意的 x , y ∈ D x,y\in D x,y∈D，及任意的 a ∈ [ 0 , 1 ] a\in [0,1] a∈[0,1]都有： f ( a x + ( 1 − a ) y ) ≤ a f ( x ) + ( 1 − a ) f ( y ) f(ax+(1-a)y)\leq af(x)+(1-a)f(y) f(ax+(1−a)y)≤af(x)+(1−a)f(y)则称函数 f ( x ) f(x) f(x)为 D D D上的凸函数。
2. 几何性质
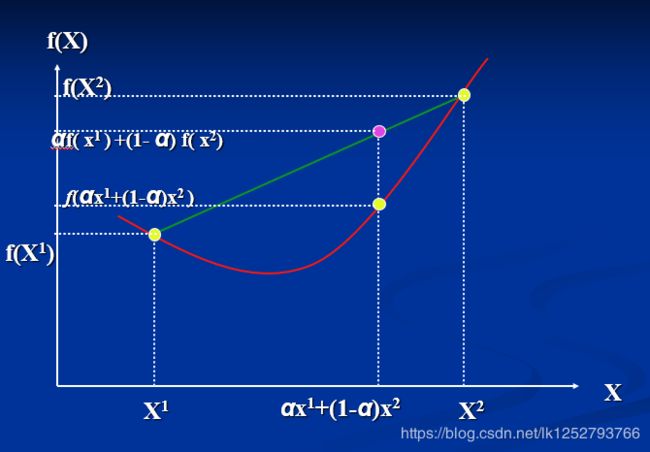
- 对于一元函数 f ( x ) f(x) f(x)，在几何上 a f ( x 1 ) + ( 1 − a ) f ( x 2 ) ( 0 ≤ a ≤ 1 ) af(x_1)+(1-a)f(x_2)(0\leq a\leq 1) af(x1)+(1−a)f(x2)(0≤a≤1)表示连接 ( x 1 , f ( x 1 ) ) , ( x 2 , f ( x 2 ) ) (x_1,f(x1)),(x_2,f(x_2)) (x1,f(x1)),(x2,f(x2))的线段。
- f ( a x 1 + ( 1 − a ) x 2 ) f(ax_1+(1-a)x_2) f(ax1+(1−a)x2)表示在点 a x 1 + ( 1 − a ) x 2 ax_1+(1-a)x_2 ax1+(1−a)x2处的函数值。
所以一元凸函数表示连接函数图形上任意两点的线段总是位于曲线弧的上方。
凸规划
1. 定义
设 D ⊆ R n D\subseteq R^n D⊆Rn为凸集， f ( x ) f(x) f(x)为 D D D上的凸函数，则称规划问题 m i n f ( x ) , ( x ∈ D ) minf(x),(x\in D) minf(x),(x∈D)为凸规划问题。
2. 性质
- 凸规划问题的任一局部极小点是全局极小点，且全体极小点的集合为凸集。
- 若 f ( x ) f(x) f(x)是凸集 D ⊆ R n D\subseteq R^n D⊆Rn上的严格凸函数，且凸规划问题 m i n f ( x ) , ( x ∈ D ) min f(x),(x\in D) minf(x),(x∈D)局部极小点 x ∗ x^* x∗存在，则 x ∗ x^* x∗是唯一的全局极小点。
例题：
解答：
相关问题
问题一：计算几何是什么？
计算几何研究的对象是几何图形。早期人们对于图像的研究一般都是先建立坐标系，把图形转换成函数，然后用插值和逼近的数学方法，特别是用样条函数作为工具来分析图形，取得了可喜的成功。然而，这些方法过多地依赖于坐标系的选取，缺乏几何不变性，特别是用来解决某些大挠度曲线及曲线的奇异点等问题时，有一定的局限性。（百度百科定义）
问题二：计算几何理论中过两点的一条直线的表达式，是如何描述的？
一般式: A x + B y + C = 0 Ax+By+C=0 Ax+By+C=0
点斜式: y − y 0 = k ( x − x 0 ) y-y0=k(x-x0) y−y0=k(x−x0)（斜率为k，且过点（x0,y0））
截距式: x / a + y / b = 1 x/a+y/b=1 x/a+y/b=1（表示与x轴、y轴相交，且x轴截距为a，y轴截距为b的直线）
斜截式: y = k x + b y=kx+b y=kx+b（表示斜率为k且y轴截距为b的直线）
两点式： ( x − x 1 ) / ( x 2 − x 1 ) = ( y − y 1 ) / ( y 2 − y 1 ) 其 中 ( x 2 ≠ x 1 , y 1 ≠ y 2 ) (x-x_1)/(x_2-x_1) = (y-y_1)/(y_2-y_1)其中(x_2\neq x_1,y_1\neq y_2) (x−x1)/(x2−x1)=(y−y1)/(y2−y1)其中(x2=x1,y1=y2)
…
问题三：凸集是什么？ 直线是凸集吗？是仿射集吗？
在凸几何中，凸集(convex set)是在凸组合下闭合的仿射空间的子集。更具体地说，在欧氏空间中，凸集是对于集合内的每一对点，连接该对点的直线段上的每个点也在该集合内。例如，立方体是凸集，但是任何中空的或具有凹痕的例如月牙形都不是凸集。特别的，凸集，实数R上（或复数C上）的向量空间中，如果集合S中任两点的连线上的点都在S内，则称集合S为凸集。
直线不是凸集但是是仿射集。
问题四：三维空间中的一个平面，如何表达？
平面方程：
A x + B y + C z + D = 0 Ax+By+Cz+D=0 Ax+By+Cz+D=0
(参数,A,B,C,D是描述平面空间特征的常数)
问题五：更高维度的“超平面”，如何表达？
超平面： H = { x ∈ R n ∣ a 1 x 1 + a 2 x 2 + . . . . . . + a n x n = b } H=\{x\in R^n|a_1x_1+a_2x_2+......+a_nx_n=b\} H={x∈Rn∣a1x1+a2x2+......+anxn=b}
超平面不完全等同于三维空间中的平面概念，在二维空间中是一条直线，三维空间中是一个平面，四维……
问题六：什么是“凸函数”定义？如何判别一个函数是凸函数？（见文章开头）
例题： f ( x ) = x 3 f(x)=x^3 f(x)=x3
是否是凸函数？
f ‘ ( x ) = 3 x 2 f^`(x)=3x^2 f‘(x)=3x2
f 2 ( x ) = 6 x f^2(x)=6x f2(x)=6x
故不是很大于0的，所以 f ( x ) f(x) f(x)不是凸函数。
问题七：什么是“凸规划”？如何判别一个规划问题是凸规划问题。举例说明？（见文章开头）
判断凸规划问题：
例：
手工推导，解答：
至此，凸规划相关问题解答完毕。