关于B树的学习总结和B+树，B*树的简介

概念

B树，英文是B-tree，是一种平衡多路树，这个不叫B减树，就是B树。

B树是一种多路树。因为他的子节点不止2个，可以是多个。

B树是一种平衡树。所谓平衡树，指的是他的左右两个子树的高度差小于等于1，而且左右子树的子树高度差也小于等于1。其实B树算是一种特殊的平衡树，因为B树的要求更高，要求左右子树高度相同，也就是说，根节点到每个叶子节点的距离都相同。

约定

1，ceil(x)，这是一个向上取整的函数，比如ceil(1.1)=2。注意这不是四舍五入，而且是得到比参数大的那个整数。

2，B树可以用阶数来定义，阶数代表了B树的节点最多可以拥有的子节点数，后面用m来代表B树的阶数。

一个m阶B树的特性

1，除了叶子节点外，树中每个节点，最少有ceil(m/2)个子节点，最多有m个子节点。

2，只要根节点不是叶子节点（那种情况只能是整个树就一个根节点），那么根节点最少有2个子节点。

3，所有叶子节点出现在同一层，即根节点到所有子节点的距离相同。

4，除了根节点之外，树中每个节点最少有ceil(m/2)-1个关键字，最多有m-1个关键字。

5，假设一个节点中有x个关键字（K1，K2，……Kx），那么需要满足以下条件：

• 有x+1个子节点（P0，P1，……Px）。
• 节点中的x个关键字升序排列，即K(n-1)
• 子节点Pn中的元素都小于Kn，都大于K(n-1)，也就是说，节点和子节点中的关键字排序是P0，K1，P1，K2，P2，……Kx，Px。

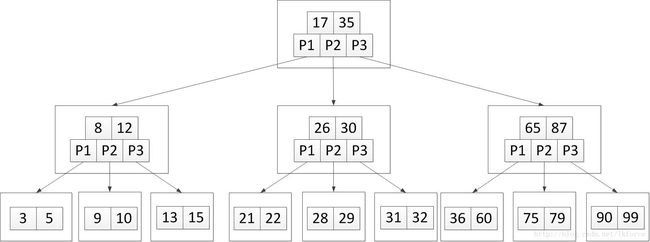
比如下面的树：

每个方框是一个节点

节点中的数字是关键字

Pn是指向子节点的指针

最上面是根节点，最下面是叶子节点，叶子节点没有指向子节点的指针

B树的查找

在上面的B树中，比如我们要找关键字32

1，比较根节点，32大于第一个关键字17，小于第二个关键字35，那么查找17和35之间的指针（P2）指向的节点（26和30那个）。

2，子节点中有关键字26和30，目标关键字32大于30，那么查找大于30的那个指针（P3）指向的节点（31和32那个）。

3，找到的子节点中有关键字31和32，在这个节点中可以找到目标关键字32。

向B树中添加关键字

向一棵m阶B树中添加关键字时，需要考虑节点中的关键字数是否超过了上限。

m阶B树每个节点最多有m-1个关键字。

如果节点在添加完关键字之后（排好序），关键字数已经达到了m，该节点将分裂成两个节点。

节点分裂的方式是，最中间的关键字向上移到父节点，大于和小于中间关键字的部分分别成为两个新的节点。可以看到，节点分裂的时候父节点得到了一个新的关键字，如果分裂前父节点关键字树已经饱和了（m-1个），会导致父节点也分裂，在最坏的情况下，分裂会一直进行到根节点，根节点一分裂，整个树的高度都会加一。

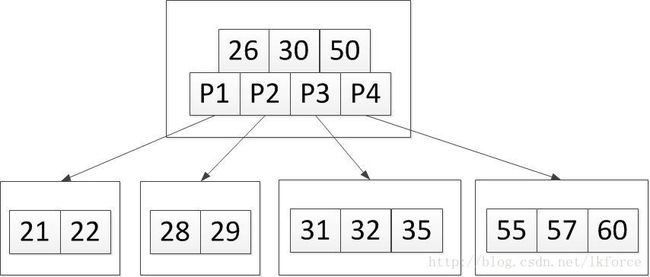
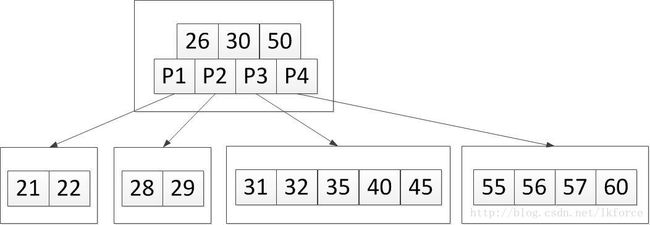
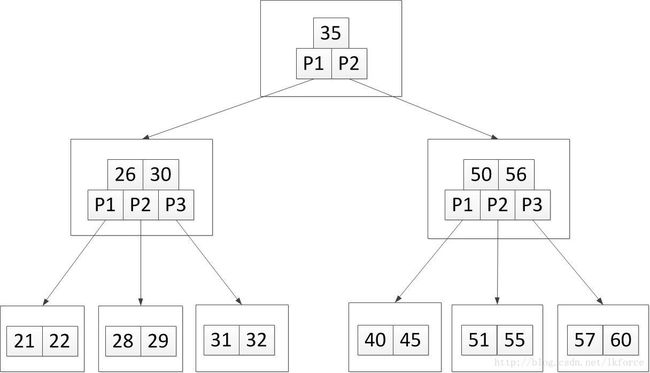
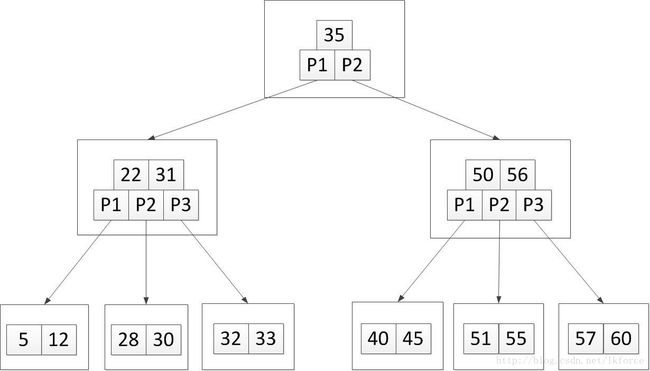
举个例子，以下五阶B树：

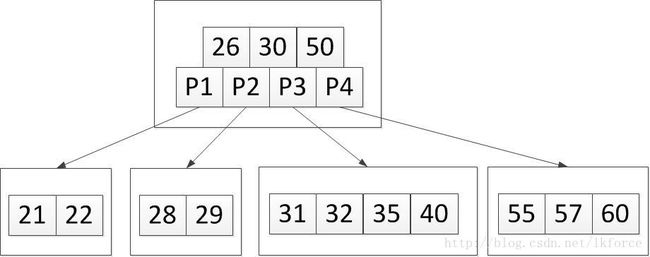
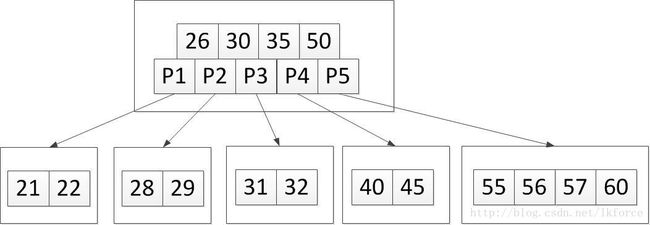
1，加入关键字40。可以很快定位到加入元素的位置是第三个叶子节点，加完之后树变成了这样：

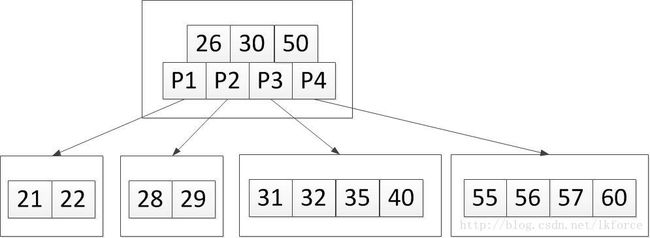
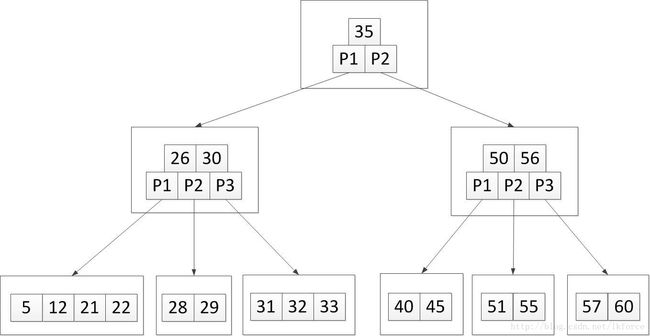
2，加入关键字56。定位到新增关键字的位置，第四个叶子节点，加完之后树变成这样：

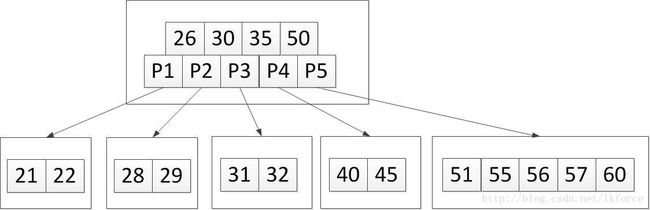
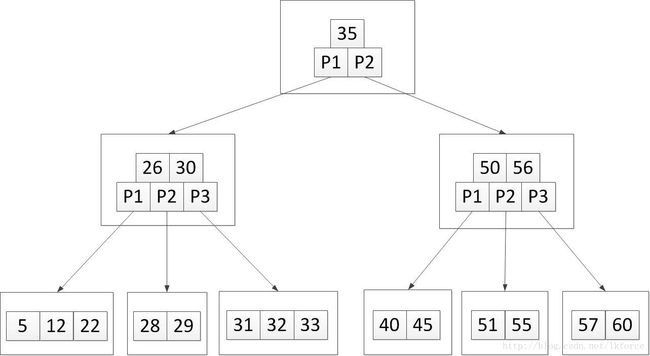
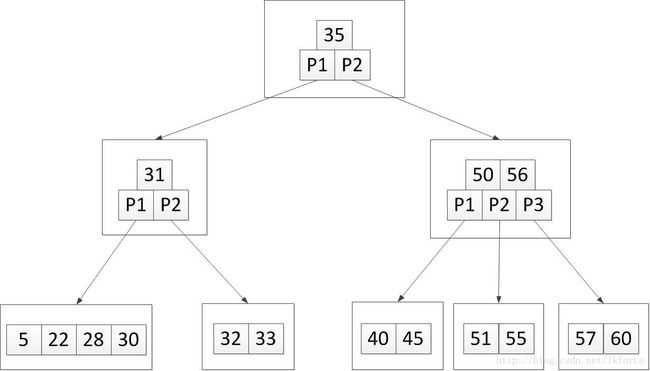
3，  加入关键字45。应该添加到第三个叶子节点，加完之后树变成这样：

还没完，5阶B树每个节点最多4个关键字，这样第三个叶子节点关键字超上限了，需要分裂。中间关键字35上升到父元素，因为35是从P3的节点来的，所以35在父节点中的位置就在小于P3的关键字30和大于P3的关键字50之间。叶子节点中小于35的关键字(31和32)组成新节点，大于35的关键字(40和45)组成新节点，然后树变成这样：

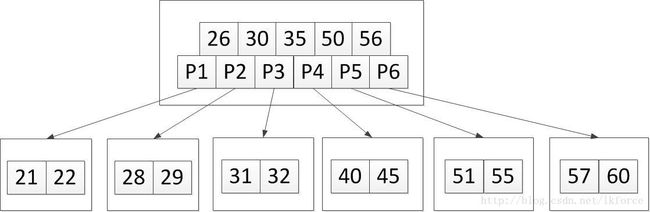
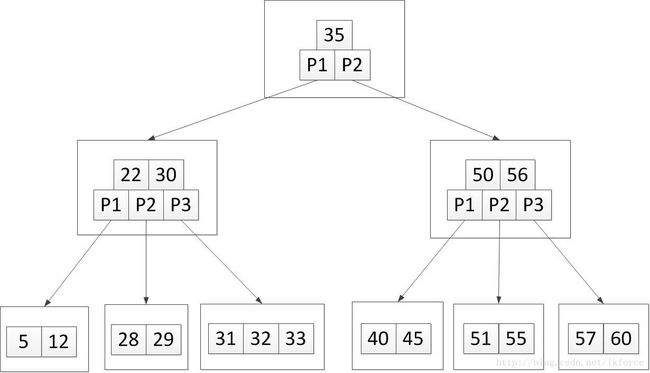
4，  加入关键字51。应该添加到第5个叶子节点，加完是这样：

第五个叶子节点关键字数超上限，分裂之后中间元素56上移到父元素，变成这样：

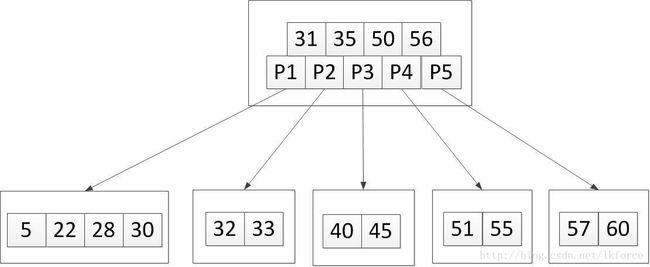
父节点得到了关键字56之后，关键字数也超上限了，也需要分裂，中间关键字35上移，大于和小于35的关键字分别形成新的节点，P3和P4指针的位置其实还是不变的，最终树变成这样：

整个树增加了一层。

从B树中删除关键字

从B树的节点中删除关键字时，需要考虑删除之后节点的关键字数量是否小于下限。

m阶B树的节点最少包含ceil(m/2)-1个关键字。

如果删除之后节点中的关键字小于下限，则需要从子树中获取关键字，或从相邻兄弟节点获取关键字，或和相邻兄弟节点合并。如果从子树获取关键字之后子树依然能保持B树的基本要求，则可以从子树中获取，否则看相邻兄弟节点元素是否富余，富余的话可以从兄弟节点获取元素，相邻兄弟节点也不富余就需要和兄弟节点合并。

从相邻兄弟节点获取关键字时，当然不是把兄弟节点的关键字直接拿过来，而是把当前节点和兄弟节点之间的那个父节点关键字拿过来，然后兄弟节点给父节点补一个关键字。

和兄弟节点合并时，需要把当前节点和兄弟节点之间的那个父节点关键字下移，然后和该节点还有兄弟节点组成新的节点，基于B树节点关键字的数量要求，这样合并出来的新节点关键字数不会超上限。这种方式在极端情况下可能会导致根节点下移合并，也就是树的层数会减少1层。

举个例子，以下五阶B树：

1，删除关键字21。最普通的情况，第一个叶子节点删除21之后，剩余关键字数量3，不需要变动，删完了变成这样：

2，删除关键字26。删除26之后节点只剩下了30一个关键字，已经不满足B树的要求，可以从子节点中获取关键字。在这个例子中只能从第一个叶子节点中获取，把叶子节点中最接近被删除关键字的元素22移到父节点，删完了是这样：

3，删除关键字29。节点删除29之后关键字只剩下了28，已经低于下限，没有子节点可以获取关键字，考虑从相邻兄弟节点获取。第一个叶子节点已经处于下限，只能从第三个叶子节点获取关键字。步骤如下：把第二叶子节点和第三叶子节点之间的父元素关键字30移到第二叶子节点，然后第三叶子节点把距离30最近的关键字31补给父节点，移完之后树是这样的：

4，删除关键字12。删除12之后第一叶子节点就只剩下了5，低于下限。在这个例子中该节点没有子节点，也不能从相邻兄弟节点中获取关键字（兄弟节点只有28和30两个关键字，不能再减少），所以只能和相邻兄弟节点合并。合并的步骤如下：把第一叶子节点和第二叶子节点之间的父节点关键字22下移，然后和第一叶子节点和第二叶子节点组成新的节点，合并完成之后的树是这样的：

此时父节点只有一个关键字31，小于下限，和直接删除该节点的关键字不同，无法再从子节点中获取关键字，在这个例子中也无法从相邻的兄弟节点获取，只能考虑和相邻兄弟节点合并，合并步骤：父节点关键字35下移，和两个子节点组成新的节点，这个节点实际上成为了根节点，整个树的高度减少了1，合并完的结果如下：

最基本的删除例子就是这样，实际上在层数比较多的情况下，删除操作可能会更复杂一些。

 

关于B+树

B+树是由B树变来的，B+树和B树有这样的区别：

1，B+树的非叶子节点不记录数据本身，只记录引用的连接。基于此特点，B+树在非叶子节点的文件会非常小。叶子节点会包含所有的关键字。

2，B+树每个叶子节点都有指向相邻的下一个兄弟叶子节点的指针。基于此特点，B+树在范围查询上的效率比B树高了很多。

3，这条区别是有争议的，有人说B+树的节点中关键字和子节点个数相同，也有人说B+树和B树一样关键字比子节点少一个。

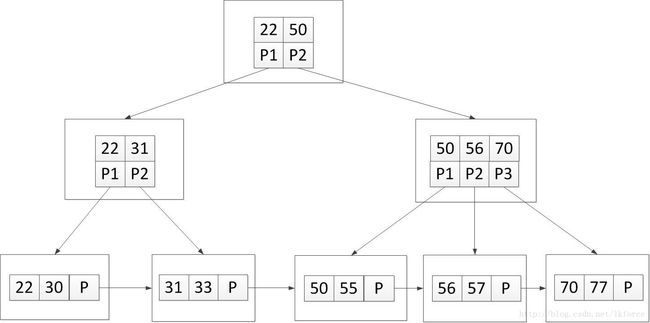
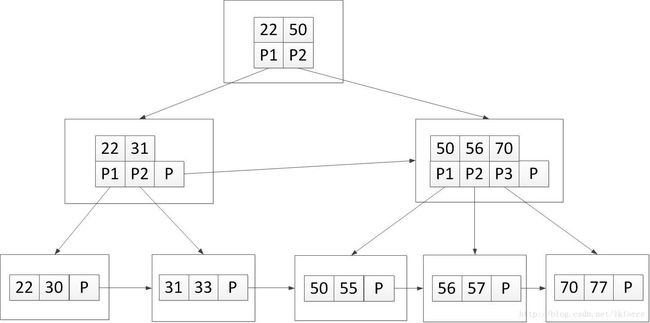
如果我们认为上述第三条中关键字和子节点个数是相同的，那B+树就是这样的：

向B+树中添加关键字时，也存在节点分裂的情况，在节点分裂时，会生成一个新的节点，把原节点中一半的元素复制到新节点，在父节点中添加指向新节点的关键字和指针。

 

关于B*树

B*树是由B+树变化来的，在B+树的基础上，B*树的非叶子节点也有指向下一个兄弟节点的指针。

B*树要求每个节点至少有2/3m个关键字，比B+树的空间利用率高。

B*树在添加关键字时也存在分裂的问题，在节点分裂时，可能会移动一部分关键字到兄弟节点中，然后在原节点中添加关键字并修改父节点的关键字和指针。如果兄弟节点已满，则新建一个节点，把原节点和兄弟节点各移1/3关键字到新建节点，然后对应修改父节点。B*树的新增关键字时的效率比B+树要低。

以下是一个B*树的例子：