看最强大脑的数字华容道,尝试理解与总结
目录
前言
华容道起源
简介
发展
华容道解法
横刀立马解(最少步数)
数字华容道
界面
解法前言
定理
定理解释
针对定理的证明
正解解法细分3种(非官方定义,都是按照自己摸索和理解定义的)
第一种:降阶法
1.还原最外层的1 2 3 4 5 9 13
2.还原第二层的 6 7 8 10 14,把三阶降为二阶
3.还原第三层:11 12 15
第二种:行解法
1.还原1 2 3 4:
2.还原5 6 7 8:
3. 还原9 13;10 14; 11 12 15
第三种:夫妻双双把家还法
前言
前段时间,新的一季《最强大脑》又开始了,第一个项目又是数字华容道,有一些选手第一关就止步了,最快的22秒,针对这个项目,个人也比较感兴趣,就买了实体数字华容道数字谜盘,捣鼓了一会儿,还原没问题。如果有个半小时时间摸索一般2~3分钟左右可以还原。是不是有更快的方法和思路呢,带着疑问去了解下华容道。
华容道起源
华容道是古老的中国民间益智游戏,以其变化多端、百玩不厌的特点与魔方、独立钻石棋一起被国外智力专家并称为“智力游戏界的三个不可思议”。它与七巧板、九连环等中国传统益智玩具还有个代名词叫作“中国的难题”。
据《资治通鉴》注释中说“从此道可至华容也”。华容道原是中国古代的一个地名,相传当年曹操曾经败走此地。由于当时的华容道是一片沼泽,所以曹操大军要割草填地,不少士兵更惨被活埋,惨烈非常。
简介
通过移动各个棋子,帮助曹操从初始位置移到棋盘最下方中部,从出口逃走。不允许跨越棋子,还要设法用最少的步数把曹操移到出口。曹操逃出华容道的最大障碍是关羽,关羽立马华容道,一夫当关,万夫莫开。关羽与曹操当然是解开这一游戏的关键。四个刘备军兵是最灵活的,也最容易对付,如何发挥他们的作用也要充分考虑周全。“华容道”有一个带二十个小方格的棋盘,代表华容道。
发展
在国内外产生了很多类似的游戏。如推箱子游戏,推箱子游戏出现在计算机中最早起源于1994年台湾省李果兆开发的仓库世家,又名仓库番,箱子只可以推, 不可以拉, 而且一次只能推动一个, 胜利条件就是把所有的箱子都推到目的地 。现在网上有很多种推箱子游戏。
华容道解法
1、历经中外科学家姜长英、藤村幸三郎、清水达雄、马丁加达纳等几十年的努力,游戏解法已由六十多年前的87步减少至81步。
2、美国一个律师托马斯.莱曼(Thomas B.Lenann)发现一个新的解法,由加德纳公布在1964年3月《科学美国人》上,有81步,称加德纳解法。
3、华容道的最快走法在中国是100步,在日本是82步。后来美国人用计算机,使用穷举法找出了最终解法,不可能有再快的解法了,81步。美国人在用计算机找到最终解法后,跟中国人开玩笑说美国一位著名的博士找到了最终解法,这位博士名叫computer。
横刀立马解(最少步数)
详细步骤:
数字华容道
数字推盘游戏(n-puzzle)是一种最早的滑块类游戏,常见的类型有十五数字推盘游戏和八数字推盘游戏等。
数字推盘游戏是由一块有凹槽的板和数个写有数字的大小相同的方块所组成。
十五数字推盘游戏的板上会有十五个方块和一个大小相当于一个方块的空位(供方块移动之用)。而八数字推盘游戏,为九宫格布局,有八个方块和一个空位。
界面
数字华容道是用尽量少的步数,尽量短的时间,将谜盘上的数字方块,按照从左到右、从上到下的顺序重新排列整齐。
解法前言
在讲解具体解法前,适当介绍下正解和镜像解。
为什么有正解和镜像解?因为随机打乱1~15个数字,并放入到谜盘中,有一半的概率是无法得到正解。
随机打乱结果去还原正解的结果会有2种:
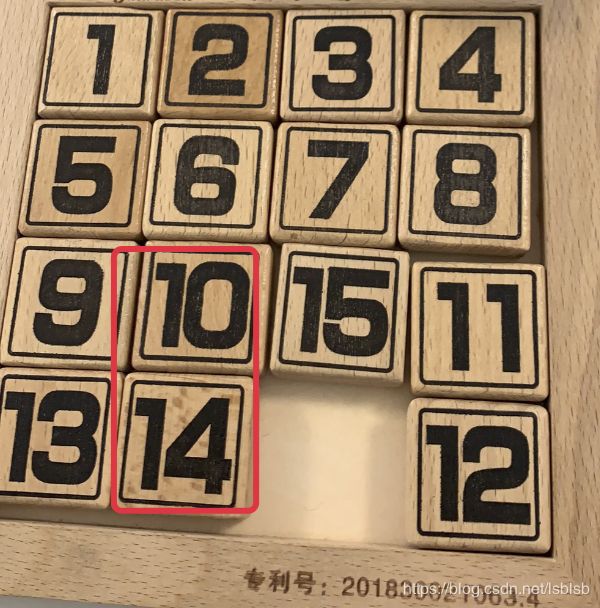
发现了吗,在第二种中,14和15是错位的,在数学界已经证明了无法还原,稍后给出大致的说明。
那么如果出现这种错位的怎么办的,从而引出了叫镜像解的思路(其实解决的是无法得到正解怎么办呢,给出另外一种玩法)。
那什么时候有正解,什么时候是镜像解呢?难道要到还原到最后一个才知道吗?这里引入线性代数中的逆序数的概念,一眼看到某个谜盘,就能判断出是否有正解。哇哦,厉害啊~ 拿小板凳看好了。
定理
图形A与图形B等价的充要条件:图形A的排列的逆序数加上0元素行号和0元素列号的奇偶性等于图形B的排列的逆序数加上0元素行号和0元素列号的奇偶性。为方便表述,把图形排列的逆序数加上0元素行号和0元素列号的奇偶性称为图形的奇偶性。
定理解释
图形A与图形B等价意思是:某一个图形变成另一个图形。(通过移动格子变化)
0元素:谜盘中空的元素,空的值为0
图形A的奇偶性= 图形数字按照从左到右,从上到下排列的逆序数 + 0元素的行号 + 0元素的列号 ===》 奇数还是偶数
图形B的奇偶性= 图形数字按照从左到右,从上到下排列的逆序数 + 0元素的行号 + 0元素的列号 ===》 奇数还是偶数
如果图形A和图形B的奇偶性相同,那么说明图形A 可以通过移动格子变化 成图形B。
排列逆序数:排列逆序数就是前面的数比这个数大,有几个比他大的数逆序数就是几,全部相加得到的值。
如:2 4 3 1 整个排列,逆序数是多少?
2前面没有是0.
4前面是2没有比它大的,是0
3前面有1个比它大的4,是1
1前面有3个比它大的分别是2 4 3 ,是3
所以 2 4 3 1 逆序数为:0 + 0 + 1 + 3 = 4
如果通过“定理解释” 对怎么排列和逆序数还有不太明白的,那就实际举例说明。
图形A:
排列:3 1 7 2 11 8 15 10 5 9 0 6 13 12 14 4
逆序数计算得到是:45 计算过程是: 0 + 1 + 0 + 2 + 0 + 1 + 0 + 2 + 5 + 3 + 10 + 6 + 1 + 2 + 1 + 11
图形A:逆序数(45) + 3(0的行号) + 3(0的列号) = 奇数
如上图B:
排列:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0
图B 奇偶性 = 逆序数(15) + 4(0的行号) + 4(0的列号) = 奇数
图形A 与 图形B 的奇偶性相同,所以,图形A可以变成图形B,图形B也可以变成图形A。
针对定理的证明
证明必要性
如果图形A与图形B等价,则图形A的奇偶性等于图形B奇偶性。
0元素和某个元素交换位置,则排列的逆序数的奇偶性就改变一次。交换后0元素的行号或者列号会加1或减1,即行号,列号之和的奇偶性也改变一次。这说明拼图的交换方式不改变图形的奇偶性,也说明拼图中至少有两组等价类,奇偶性不同的图形不等价。
证明充分性
如果图形A的奇偶性等于图形B的奇偶性,则图形A,B等价。
如果证明了拼图只有两组等价类,从必要性的证明过程可知,奇性图形是一组等价类,偶性是一组。从而证明了充分性。
先考虑一般的排列1 2 3 ... N。某个元素连续与后面M相邻的元素交换位置,称为向后M步移动。如排列:1 2 3 4 5 6。元素2的向后3步移动,排列变成1 3 4 5 2 6。同样的方式定义向前M步移动。如果排列A能够通过有限向前M步移动和向后M步移动变成排列B,称排列A与排列B M步等价。容易看出这也是等价关系。
正解解法细分3种(非官方定义,都是按照自己摸索和理解定义的)
第一种:降阶法
总体思路:把 4*4 的谜盘 变成 3*3,然后再变成 2*2
具体步骤:
1.还原最外层的1 2 3 4 5 9 13,把四阶降为三阶(如下图)
2.还原第二层的 6 7 8 10 14,把三阶降为二阶(如下图)
3.还原第三层:11 12 15(如下图)
具体解法:
1.还原最外层的1 2 3 4 5 9 13
还原1 2 3,无压力,直接一个一个的把他们送到对应的位置即可。
还原4(如下4张图):把4放到3的下面,然后把2 3 4 逆时针旋转;右边顶角空出来,3 4 右移,2 还原
还原5 无压力
还原9 13 :按照如下图 13,9 排列好,然后下移完成
2.还原第二层的 6 7 8 10 14,把三阶降为二阶
还原 6 7 无压力
还原8 与 还原 4 类似:8放到7的下面
还原10 14:把14放到9旁边,然后10放到14旁边,然后下来还原
3.还原第三层:11 12 15
直接转一圈即可还原
第二种:行解法
总体思路:先还原第一行: 1 2 3 4 ,然后还原第二行:5 6 7 8
如果直接还原第三行, 那么第四行存在不对的情况,很难处理。
所以第三行和第四行一起处理:按照列列还原。即:9 13;10 14; 11 12 15
具体解法:
1.还原1 2 3 4:
通过循环运动,很好排出1 2 3;
4的还原,参考降阶法中的4的还原
2.还原5 6 7 8:
通过循环运动,很好排出5 6 7;
8的还原,参考4的还原
3. 还原9 13;10 14; 11 12 15
思路一:先把9 13 放一起放到如图位置。
10 14:思路与9 13 一致
11 12 15:直接转一圈即可
思路二:把9,10和 11 12 放到如图位置,然后把13 14 15放到如图位置,
第三种:夫妻双双把家还法
思路:与行解法一致,细节上略有不同。
还原4方法不同(垂直法):那么3比作是你,4比作是你对象。
1.把3和4先放到如图位置(间隔1行斜对角)
2.把3(你)主动到你对象上方,即顺时针或逆时针转一圈即可
3.依偎在一起,从此不分离(3和4往上左,挪出空间给34归位)
还原9 13方法不同(水平法):要把13放到9下面,9是你,13是你对象
1.先放到如图位置(间隔一列斜对角)
2.把9(你)主动到你对象旁边,即顺时针或逆时针转一圈即可
3.依偎在一起,从此不分离(9和13往左上,挪出空间给9 13归位)
其他的还原参考垂直法和水平法。