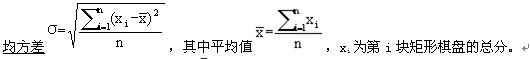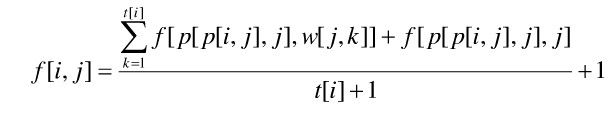dp泛做1
这里的dp范做根据网上的动态归法分析和网上的有个100个dp方程做的,题解很多是原版,没怎么动,有些是别人的一些其他做法,还有一些自己的想法。如果看到题解很别人一样,那就是摘自别人的。且这里只是一半。
由于本文有些摘自网上,如有原主看到不想在此贴出的,请说明,将会撤出。
如此文方法错误,或者冒犯某些原博主的文章还请见谅,还请指出,非常感谢
机器分配(HNOI’95)
0-1背包变形tyvj1089smrtfun
最长不下降序列(HNOI’97)
石子合并(NOI’95)
凸多边形三角划分(HNOI’97)
乘积最大(noip’2000)
系统可靠性(HNOI’98)
过河(noip’2005)
加分二叉树(noip’2003)
选课(CTSC’98)
砝码称重(noip’96)
核电站问题
数的划分(noip2001)
最大01矩阵
最大子矩阵(Scoi’05)
加+-被k整除(poj1745)
方块消除(poj1390)
装箱问题(noip2001)
数字三角形
晴天小猪历险记同一阶段上暴力动态规划
小胖办证(双向动态规划1,数字三角形)
马拦卒过河noip2002
打砖块(tyvj’1505)
打鼹鼠(CscIIvijos1441)
贪吃的九头龙(NOI2002)
状态压缩dp炮兵阵地(poj1185)
常用递推式子
排列组合中的环形染色问题
隐形的翅膀-线性搜索
陨石的秘密(NOI’2001)
合唱队形(noi2004)
今明的预算方案(noip2006)
花店橱窗布置(IOI’99)
化工厂装箱员
欢乐的聚会spfa+dp
小胖守皇宫(treedp)
活动安排(xtu2012)
有向树k中值问题
CEOI1998 Substract
古城之谜(Noi2000)
单词的划分(tyvj1102)
统计单词个数(Noip2001)
括号序列—tyvj1193
括号序列poj1141
棋盘分割(NOI’99,poj1191)
聪聪和可可(noi2005)
血缘关系
决斗(rqnoj458)
跳舞家怀特先生(tyvj1211)
积木游戏(NOI’97)
逃学的小孩(NOI2003)
机器分配(HNOI’95)
一、问题描述
总公司拥有高效生产设备M台,准备分给下属的N个公司。各分公司若获得这些设备,可以为国家提供一定的盈利。问:如何分配这M台设备才能使国家得到的盈利最大?求出最大盈利值。其中M《=15,N〈=10。分配原则:每个公司有权获得任意数目的设备,但总台数不得超过总设备数M。保存数据的文件名从键盘输入。
数据文件格式为:第一行保存两个数,第一个数是设备台数M,第二个数是分公司数N。接下来是一个M*N的矩阵,表明了第I个公司分配J台机器的盈利。
二、分析
这是一个典型的动态规划试题。用机器数来做状态,数组F[I,J]表示前I个公司分配J台机器的最大盈利。则状态转移方程为
F[I,J]=Max{F[I-1,K] + Value[I,J-K]} (0〈=K〈=J〉
0-1背包变形tyvj1089smrtfun
一、问题描述
现有N个物品,第i个物品有两个属性A_i和B_i。在其中选取若干个物品,使得sum{A_i + B_i}最大,同时sum{A_i},sum{B_i}均非负(sum{}表示求和)。
输入:第一行,一个整数,表示物品个数N。 接下来N行,每行两个整数,表示A_i和B_i。
输出:一个整数,表示最大的sum{A_i + B_i}。
N <= 100 , |A_i| <= 1000 , |B_i| <= 1000
二、分析
首先就是表示状态 f[i]表示当sum{b}为i时sum{a}的最大值,那么sum{b}就相当于背包的体积(可以为负),b[i]就相当于物品的体积(但可以为负值),那没有一个确定的背包体积怎么办呢。。就在线的扩展MAX,初始化MAX=0;比如说第一个b[i];放进去的时候就扩展一下MAX+=b[i];把Ai的和当背包的重量,把Bi的和当成价值来做,每次重量考察Ai和的最小到最大
对于f[]的上限注意了,可不是经典的零。。因为体积(sum{b[i]})可以为负所以就要设置一个MIN来表示其上限。不断地更新MIN,类似MAX那样更新。
最后把j从0到MAX枚举一下
对于当w[i]<0的时候为什么要把for循环那个MIN to MAX+w[i]而不是AX to MIN+w[i];疑问:MIN to MAX+w[i]不就是放无数次,成为完全背包了吗?答:因为w[i]<0.
f[j]:=max(f[j], f[j-a[i]]+b[i])
最长不下降序列(HNOI’97)
一、问题描述
设有整数序列b1,b2,b3,…,bm,若存在i1 输入:整数序列 输出:最大长度n和所有长度为n的序列个数Total 二、分析 LIS(Longest Increasing Subsequence)最长上升(不下降)子序列,有两种算法复杂度为O(n*logn)和O(n^2)。在上述算法中,若使用朴素的顺序查找在D1..Dlen查找,由于共有O(n)个元素需要计算,每次计算时的复杂度是O(n),则整个算法的时间复杂度为O(n^2),与原来算法相比没有任何进步。但是由于D的特点(2),在D中查找时,可以使用二分查找高效地完成,则整个算法时间复杂度下降为O(nlogn),有了非常显著的提高。需要注意的是,D在算法结束后记录的并不是一个符合题意的最长上升子序列!算法还可以扩展到整个最长子序列系列问题。有两种算法复杂度为O(n*logn)和O(n^2) (a[1]...a[n] 存的都是输入的数) 2、若从a[n-1]开始查找,则存在下面的两种可能性: (1)若a[n-1] < a[n] 则存在长度为2的不下降子序列 a[n-1],a[n]. (2)若a[n-1] > a[n] 则存在长度为1的不下降子序列 a[n-1]或者a[n]。 3、一般若从a[t]开始,此时最长不下降子序列应该是按下列方法求出的: 在a[t+1],a[t+2],...a[n]中,找出一个比a[t]大的且最长的不下降子序列,作为它的后继。 4、为算法上的需要,定义一个数组: d:array [1..n,1..3] of integer; d[t,1]表示a[t] d[t,2]表示从i位置到达n的最长不下降子序列的长度 d[t,3]表示从i位置开始最长不下降子序列的下一个位置 最长不下降子序列的O(n*logn)算法 先回顾经典的O(n^2)的动态规划算法,设A[t]表示序列中的第t个数,F[t]表示从1到t这一段中以t结尾的最长上升子序列的长度,初始时设F[t] = 0(t = 1, 2,..., len(A))。则有动态规划方程:F[t]= max{1, F[j] + 1} (j = 1, 2, ..., t - 1, 且A[j] < A[t])。 现在,我们仔细考虑计算F[t]时的情况。假设有两个元素A[x]和A[y],满足 (1)x < y < t (2)A[x] < A[y] < A[t] (3)F[x] =F[y] 此时,选择F[x]和选择F[y]都可以得到同样的F[t]值,那么,在最长上升子序列的这个位置中,应该选择A[x]还是应该选择A[y]呢? 很明显,选择A[x]比选择A[y]要好。因为由于条件(2),在A[x+1] ... A[t-1]这一段中,如果存在A[z],A[x] < A[z] < a[y],则与选择A[y]相比,将会得到更长的上升子序列。 再根据条件(3),我们会得到一个启示:根据F[]的值进行分类。对于F[]的每一个取值k,我们只需要保留满足F[t] = k的所有A[t]中的最小值。设D[k]记录这个值,即D[k] = min{A[t]} (F[t] = k)。 注意到D[]的两个特点: (1) D[k]的值是在整个计算过程中是单调不上升的。 (2) D[]的值是有序的,即D[1]< D[2] < D[3] < ... < D[n]。 利用D[],我们可以得到另外一种计算最长上升子序列长度的方法。设当前已经求出的最长上升子序列长度为len。先判断A[t]与D[len]。若A[t] > D[len],则将A[t]接在D[len]后将得到一个更长的上升子序列,len = len + 1, D[len] = A[t];否则,在D[1]..D[len]中,找到最大的j,满足D[j] < A[t]。令k = j + 1,则有D[j] < A[t] <= D[k],将A[t]接在D[j]后将得到一个更长的上升子序列,同时更新D[k] = A[t]。最后,len即为所要求的最长上升子序列的长度。 在上述算法中,若使用朴素的顺序查找在D[1]..D[len]查找,由于共有O(n)个元素需要计算,每次计算时的复杂度是O(n),则整个算法的时间复杂度为O(n^2),与原来的算法相比没有任何进步。但是由于D[]的特点(2),我们在D[]中查找时,可以使用二分查找高效地完成,则整个算法的时间复杂度下降为O(nlogn),有了非常显著的提高。需要注意的是,D[]在算法结束后记录的并不是一个符合题意的最长上升子序列! 这个算法还可以扩展到整个最长子序列系列问题,整个算法的难点在于二分查找的设计,需要非常小心注意。 介绍二: 最长上升子序列LIS算法实现 最长上升子序列问题是各类信息学竞赛中的常见题型,也常常用来做介绍动态规划算法的引例,笔者接下来将会对POJ上出现过的这类题目做一个总结,并介绍解决LIS问题的两个常用算法(n^2)和(nlogn). 问题描述:给出一个序列a1,a2,a3,a4,a5,a6,a7....an,求它的一个子序列(设为s1,s2,...sn),使得这个子序列满足这样的性质,s1 例如有一个序列:1 7 35 9 4 8,它的最长上升子序列就是 13 4 8 长度为4. 算法1(n^2):我们依次遍历整个序列,每一次求出从第一个数到当前这个数的最长上升子序列,直至遍历到最后一个数字为止,然后再取dp数组里最大的那个即为整个序列的最长上升子序列。我们用dp[i]来存放序列1-i的最长上升子序列的长度,那么dp[i]=max(dp[j])+1,(j∈[1, i-1]); 显然dp[1]=1,我们从i=2开始遍历后面的元素即可。 算法2(nlogn):维护一个一维数组c,并且这个数组是动态扩展的,初始大小为1,c[i]表示最长上升子序列长度是i的所有子串中末尾最小的那个数,根据这个数字,我们可以比较知道,只要当前考察的这个数比c[i]大,那么当前这个数一定能通过c[i]构成一个长度为i+1的上升子序列。当然我们希望在C数组中找一个尽量靠后的数字,这样我们得到的上升子串的长度最长,查找的时候使用二分搜索,这样时间复杂度便下降了。 石子合并(NOI’95) 一、问题描述 输入数据: 文件名由键盘输入,该文件内容为: 第一行为石子堆数N; 第二行为每堆石子数,每两个数之间用一空格分隔. 输出数据 : 输出文件名为OUTPUT.TXT 从第1至第N行为得分最小的合并方案. 第N+1行为空行.从N+2到2N+1行是得分最大的合并方案. 每种合并方案用N行表示,其中第i行(1≤i≤N)表示第i次合并前各堆的石子数(依顺时钟次序输出,哪 一堆先输出均可). 要求将待合并的两堆石子数以相应的负数表示,以便识别,参见MODEL2.TXT 参考输入文件EXAMPLE2.TXT 4 4 5 9 4 参考输出文件MODEL2.TXT -4 5 9 -4 -8 -5 9 -9 -13 -22 4 -5 -9 4 4 -14 -4 -4 –18 -22 二、分析 看到本题,容易想到使用贪心法,即每次选取相邻最大或最小的两堆石子合并。 然而这样做对不对呢?看一个例子。 N=5 石子数分别为3 4 6 5 4 2。 用贪心法的合并过程如下: 第一次 3 4 65 4 2得分 5 第二次 5 4 65 4得分9 第三次 9 6 5 4得分9 第四次 9 6 9得分15 第五次 15 9得分24 第六次24 总分:62 然而仔细琢磨后,发现更好的方案: 第一次3 4 65 4 2得分 7 第二次7 6 54 2得分13 第三次13 5 4 2得分6 第四次13 5 6得分11 第五次 13 11得分24 第六次24 总分:61 显然,贪心法是错误的。 为什么? 显然,贪心只能导致局部的最优,而局部最优并不导致全局最优。 仔细分析后,我们发现此题可用动态规划进行解决。 我们用data[I,j]表示将从第i颗石子开始的接下来j颗石子合并所得的分值, max[i,j]表示将从第i颗石子开始的接下来j颗石子合并可能的最大值,那么: max[I,j] = max(max[i, k] + max[i + k, j – k] + data[I,k] + data[I + k, j – k]) (2<=k<=j) max[i,1] = 0 同样的,我们用min[i,j]表示将第从第i颗石子开始的接下来j颗石子合并所得的最小值,可以得到类似的方程: min[I,j] = min(min[i, k] + min[i + k, j – k] + data[I,k] + data[I + k, j – k]) (0<=k<=j) min[I,0] = 0 这样,我们完美地解决了这道题。空间复杂度为O(n2),时间复杂度也是O(n2)。 动态规划思路: 第四阶段:四四合并的拆分方法用三种,同理求出三种分法的得分,取其最优即可。以后第五阶段、第六阶段依次类推,最后在第六阶段中找出最优答案即可 凸多边形三角划分(HNOI’97) 一、试题描述 给定一个具有N(N<50)个顶点(从1到N编号)的凸多边形,每个顶点的权均已知。问如何把这个凸多边形划分成N-2个互不相交的三角形,使得这些三角形顶点的权的乘积之和最小? 输入文件:第一行 顶点数N 第二行 N个顶点(从1到N)的权值 输出格式:最小的和的值 各三角形组成的方式 输入示例:5 121 122 123 245 231 输出示例:The minimum is :12214884 The formation of 3 triangle: 3 4 5, 15 3, 1 2 3 二、试题分析 这是一道很典型的动态规划问题。设F[I,J](I F[I,J]=Min{F[I,K]+F[K,J]+S[I]*S[J]*S[K]} (I 目标状态为:F[1,N] 但我们可以发现,由于这里为乘积之和,在输入数据较大时有可能超过长整形甚至实形的范围,所以我们还需用高精度计算,但这是大家的基本功,程序中就没有写了,请读者自行完成。 乘积最大(noip’2000) 问题描述: 一道题目:设有一个长度N的数字串,要求选手使用K个乘号将它分成K+1个部分,找出一种分法,使得这K+1个部分的乘积能够为最大。同时,为了帮助选手能够正确理解题意,主持人还举了如下的一个例子: 有一个数字串: 312,当N=3,K=1时会有以下两种分法: 1)3*12=36 2)31*2=62 这时,符合题目要求的结果是: 31*2=62 输入:程序的输入共有两行: 第一行共有2个自然数N,K(6<=n<=40,1<=k<=6) 第二行是一个K度为N的数字串。 输出:结果显示在屏幕上,相对于输入,应输出所求得的最大乘积(一个自然数)。 输入 4 2 1231 输出 62 分析: 设字符串长度为n,乘号数为k,如果n=50,k=1时,有(n-1)=49种不同的乘法,当k=2时,有C(2,50-1)=1176种乘法,既C(k,n-1)种乘法,当n、k稍微大一些的时候,用穷举的方法就不行了。 设数字字符串为a1a2…an K=1 时:一个乘号可以插在a1a2…an中的n-1个位置,这样就得到n-1个子串的乘积: a1*a2…an, a1a2*a3…an, …, a1a2…a n-1*an( 这相当于是穷举的方法) 此时的最大值= max{a1*a2…an,a1a2*a3…an, …, a1a2…a n-1*an } K=2时,二个乘号可以插在a1a2…an中n-1个位置的任两个地方, 把这些乘积分个类,便于观察规律: ①最后一个数作为被乘数: a1a2 …*a n-1*an , a1a2 …*a n-2 a n-1*an , a1*a2 …a n-3 a n-2 a n-1*an 设符号F[n-1,1]为在前n-1个数中插入一个乘号的最大值,则的最大值为F[n-1,1]*an ②最后2个数作为被乘数: a1a2 …*a n-2*a n-1an , a1a2 …*a n-3 a n-2* an-1 an , a1*a2 …an-3 a n-2*an-1an 设符号F[n-2,1]为在前n-2个数中插入一个乘号的最大值,则的最大值为F[n-2,1]*an-1an ③最后3个数作为被乘数: 设符号F[n-3,1]为在前n-3个数中插入一个乘号的最大值,则最大值为F[n-3,1]+an-2an-an …… a3~an作为被乘数:F[2,1]*a3 …an-2an-1an 此时的最大乘积为: F[n,k]=max{F[n-1]*an,F[n-2,1]*an-1an,F[n-3,1]*an-2an-1an,F[2,1]*a3…an-2an-1an} 设F[i,j]表示在 i 个数中插入 j 个乘号的最大值,g[i,j]表示从ai到aj的数字列,则可得到动规方程: F[I,j]= max{F[I-1,j-1]*g[I,I],F[I-2,j-1]*g[I-1,I],F[I-3,j-1]*g[I-2,I], …,F[j,j-1]*g[j+1,I]}(1<=I<=n, 1<=j<=k) 边界: F[I,0] =g[1,I] (数列本身) 阶段:子问题是在子串中插入j-1,j-2……1,0个乘号,因此乘号个数作为阶段的划分(j个阶段) 状态:每个阶段随着被乘数数列的变化划分状态。 决策:在每个阶段的每种状态中做出决策。 还有2个问题需要注意: (1)输入的字符需要进行数值转换 (2)由于乘积可能很大,所以可以使用大数类型 参考程序 系统可靠性(HNOI’98) 一、问题描述: 给定一些系统备用件的单价Ck,以及当用Mk个此备用件时部件的正常工作概率Pk(Mk),总费用上限C。求系统可能的最高可靠性。 输入:第一行:n C 第二行:C1 P1(0) P1(1) … P1(X1) (0<=X1<=[C/Ck]) … 第 n 行:Cn Pn(0) Pn(1) … Pn(Xn) (0<=Xn<=[C/Cn]) 输出:最大可靠性的值 样例 输入: 2 20 3 0.6 0.65 0.7 0.75 0.8 0.85 0.9 5 0.7 0.75 0.8 0.8 0.9 输出:0.6375 二、算法分析 1.证明这个问题符合最优化原理。可以用反证法证明之。假设用money的资金购买了前I项备用件,得到了最高的系统可靠性,而且又存在如下情况:对于备用件I,设要买Ki个,则可用的资金还剩余money– Ci*Ki,用这些钱购买前(I-1)项备用件,如果存在一种前(I-1)种备用件的购买方案得到的系统可靠性比当前得到的要高,那么这个新的方案会使得整个前I项备用件组成的系统可靠性比原先的更高,与原假设矛盾。所以可以证明这个问题符合最优化原理。 2.证明这个问题符合无后效性原则。 3.综上所述,本题适合于用动态规划求解。 4.递推方程及边界条件: F[I,money] :=max { F[I-1,money – C[I]*K[I] ] } (0<=K[I]<=C div Ci ) 三、参考程序 过河(noip’2005) 一、 问题描述 在河上有一座独木桥,一只青蛙想沿着独木桥从河的一侧跳到另一侧。在桥上有一些石子,青蛙很讨厌踩在这些石子上。由于桥的长度和青蛙一次跳过的距离都是正整数,我们可以把独木桥上青蛙可能到达的点看成数轴上的一串整点:0,1,……,L(其中L是桥的长度)。坐标为0的点表示桥的起点,坐标为L的点表示桥的终点。青蛙从桥的起点开始,不停的向终点方向跳跃。一次跳跃的距离是S到T之间的任意正整数(包括S,T)。当青蛙跳到或跳过坐标为L的点时,就算青蛙已经跳出了独木桥。 题目给出独木桥的长度L,青蛙跳跃的距离范围S,T,桥上石子的位置。你的任务是确定青蛙要想过河,最少需要踩到的石子数。 对于30%的数据,L <= 10000; 对于全部的数据,L <= 10^9。 输入:第一行有一个正整数L(1 <= L <= 10^9),表示独木桥的长度。第二行有三个正整数S,T,M,分别表示青蛙一次跳跃的最小距离,最大距离,及桥上石子的个数,其中1 <= S <= T <= 10,1 <= M <= 100。第三行有M个不同的正整数分别表示这M个石子在数轴上的位置(数据保证桥的起点和终点处没有石子)。所有相邻的整数之间用一个空格隔开 输出:输出只包括一个整数,表示青蛙过河最少需要踩到的石子数。 样例:10 2 3 5 2 3 56 7 输出:2 分析: 1.分s=t和s 这题因为 1 <= L <= 10^9 L非常大,只能进行状态压缩。如果 L小到可以开数组,我们可以设一个数组Dp[L_MAX]保存每个子状态,从后往前DP,Dp[n] 表示从坐标位置 n 跳到或者跳过终点的最优解(局部最优),求Dp[n-1],Dp[n-1] = min{Dp(n-1+minJump ~ n-1+maxJump)},minJump表示青蛙最小的跳数,maxJump表示青蛙最大的跳数,如果 n-1 位置有石头则Dp[n-1]=Dp[n-1]+1. 比如对于示例: 10 2 3 5 2 3 56 7 首先我们初始化数组,Dp[]={0},从坐标位置7开始算,Dp[7]=min{Dp(2+7,3+7)}=0,因为7位置有石头所以Dp[7]=Dp[7]+1=1,同理,Dp[6]=1,Dp[5]=1,Dp[4] = min{Dp(4+2,4+3)} = 1,因为5位置没有石头所以Dp[4]不用加1,最后可求得 Dp[] = {2,1,2,2,1,1,1,1,0,0,0 ……},Dp[0]即为全局的最优解,表示从起点跳到或者跳过终点青蛙最少要踩到的石头数目。 这题因为L很大,子状态不能全部保存,我们观察到,当求Dp[n]的值时用到的状态只有 Dp(n+minJump,n+maxJump)所以我们可以不用全部保存每个坐标位置的Dp值,而只要保存从n位置之后最多maxJump个坐标的Dp值即可。为此我们可设Dp[maxJump](对本题可设Dp[10]),注意这里的下标不表示坐标位置,我们可用一个变量nHeadStart跟踪坐标位置,当求n位置的Dp值时,nHeadStart=n+1。到这里我们解决了空间问题,真正难理解的是下面的状态压缩。 假如测试数据是: 1000000000 2 5 5 2 6 510 99999999 99999999这个位置的Dp值我们知道是 1,而该位置前面有99999999-10个位置都没有石头,我们不可能也没有时间去求所有这些中间位置的Dp值,但是10位置的值却与这中间的有关,HowCan I do ???假如有这样一组Dp值,Dp[]={25 1 3} 我们观察到单minJump != maxJump时,因为每次都取最小值所以经过有限步运算后,Dp={1 1 1 1},即所有的Dp值都变成开始计算时的最小值。变化经过如下 数据:minJump=2, maxJump=3,Dp[]={2,5,1,3} Dp[]={1,2,5,1} Dp[]={1,2,2,5} Dp[]={2,1,2,2} Dp[]={1,2,1,2} Dp[]={1,1,2,1} Dp[]={1,1,1,2} Dp[]={1,1,1,1} 即从当前位置到前面 7 个及 7 个以前的空位(没有石头),我们断定Dp[]={1,1,1,1} 因此,对 2 6 5 10 99999999,我们可以知道从 11 位置开始,Dp[]={0,0,0,0,0}(只需保存maxJump个)前面的就好做了。经过几步的空位可以达到稳定状态(我称Dp数组值不再变化的状态为稳定态),我们有两种方法 其一:每求一个空位后我们求Dp数组中的最值,如果最大和最小值相等就达到稳定态了。这种方 法因为每次都要求最值,因此当maxJump比较大的时候不适合。 其二:我们可以断定如果当前位置之前至少有maxJump*maxJump个空位,就一定会出现稳定态(请读者自己理解 这样我们遇到空位大于等于maxJump*maxJump时直接设Dp数组为最小值。 上面的是minJump != maxJump的情况,当minJump==maxJump时,假如Dp[]={0,0,1} 数据:minJump=3, maxJump=3,Dp[]={0,0,1},Dp的变化情况如下: Dp[]={1,0,0} Dp[]={0,1,0} Dp[]={0,0,1} ...... 出现重复的情况,且min{Dp[]} != max{Dp[]},因此不能按minJump !=maxJump的情况处理。这种情况只要将重复出现的位去掉即可,比如上面的如果当前位置前有 4 个空位,前三个不用计算,因为到第三个位置的Dp值和当前的Dp值一样。 Dp[]数组的下标变化大家可以参考循环队列的情况。 关于压缩空长条步数的证明 对于步幅s到t 若目标位置距起始点距离D≥s×(s+1)则一定可以到达目标点 证明: 设一次可以走p步或p+1 方便起见,我们取起始位置为坐标0点 那么p×(p-1)点一定可以达到(每次走p的距离,走p-1次) 因为我们也可以每次走p+1步 所以可以通过将一次p距离的行走替换为p+1距离的行走来实现总距离+1 比如说我们要达到p×(p-1)+1点我们只需要走p-2次p的距离和一次p+1的距离即可到达 我们整理两个表达式p×(p-1)+1和(p-2)×p+(p+1)就可证明上述正确 现在我们从(p-1)×p位置开始逐一推算可行性 (p-1)×p+1=(p-2)×p+(p+1) (p-1)×p+2=(p-3)×p+(p+1)×2 (p-1)×p+3=(p-4)×p+(p+1)×3 …… (p-1)×p+(p-1)=(p-p)×p+(p+1)(p-1) 我们已经用光了所有可以替换的p距离行走。 那么(p-1)×p+p如何实现呢? 对上面多项式整理得:p×p 显然我们只需要进行p次p距离的行走就可以到达目标 也就是说我们通过用p+1代换p的方法前进p-1步 在前进第p步时重新整合成关于p的多项式(一定是p的倍数)如此往复。 而我们要前进p-1步至少需要p-1个p。所以下限为p×(p-1) 至此,命题得证。 加分二叉树(noip’2003) 一、问题描述 设一个n个节点的二叉树tree的中序遍历为(l,2,3,…,n),其中数字1,2,3,…,n为节点编号。每个节点都有一个分数(均为正整数),记第j个节点的分数为di,tree及它的每个子树都有一个加分,任一棵子树subtree(也包含tree本身)的加分计算方法如下: subtree的左子树的加分× subtree的右子树的加分+subtree的根的分数 若某个子树为主,规定其加分为1,叶子的加分就是叶节点本身的分数。不考虑它的空子树。 试求一棵符合中序遍历为(1,2,3,…,n)且加分最高的二叉树tree。要求输出; 1)tree的最高加分 2)tree的前序遍历 输入格式 InputFormat 第1行:一个整数n(n<30),为节点个数。 第2行:n个用空格隔开的整数,为每个节点的分数(分数<100)。 输出格式 OutputFormat 第1行:一个整数,为最高加分(结果不会超过4,000,000,000)。 第2行:n个用空格隔开的整数,为该树的前序遍历。 样例输入:5 5 7 1 2 10 样例输出:5 5 7 1 2 10 二、分析: 区间DP。 用f[i,j]表示合并[i,j]这段区间的最大加分,k为根,则有 f[i,j]:=max(f[i,k]*f[k,j]+score[k]);{i<=k<=j} 边界是空树的加分为1,单位区间的最大加分为本身的加分。 目标为f[1,n]; 由于要输出方案,所以在转移时记录转移的k.最后递归输出即可。 注意就是先循环长度,再枚举开始位置,用长度和开始位置求出结束位置之后再枚举k。因为转移的时候,要求比当前区间短的区间都要知道。 ------------------ 先画画这种树算算样例 发现每个树划分为左右子数后 左右子树也是按照同样的方法划分 形成了重叠子结构 马上想到区间DP 配合四边形不等式O(N*N) 选课(CTSC’98) 一、问题描述 大学里实行学分。每门课程都有一定的学分,学生只要选修了这门课并考核通过就能获得相应的学分。学生最后的学分是他选修的各门课的学分的总和。 每个学生都要选择规定数量的课程。其中有些课程可以直接选修,有些课程需要一定的基础知识,必须在选了其它的一些课程的基础上才能选修。例如,《数据结构》必须在选修了《高级语言程序设计》之后才能选修。我们称《高级语言程序设计》是《数据结构》的先修课。每门课的直接先修课最多只有一门。两门课也可能存在相同的先修课。为便于表述每门课都有一个课号,课号依次为1,2,3,……。下面举例说明 课号 先修课号 学分 1 无 1 2 1 1 3 2 3 4 无 3 5 2 4 上例中1是2的先修课,即如果要选修2,则1必定已被选过。同样,如果要选修3,那么1和2都一定已被选修过。 学生不可能学完大学所开设的所有课程,因此必须在入学时选定自己要学的课程。每个学生可选课程的总数是给定的。现在请你找出一种选课方案,使得你能得到学分最多,并且必须满足先修课优先的原则。假定课程之间不存在时间上的冲突。 输入 输入文件的第一行包括两个正整数M、N(中间用一个空格隔开)其中M表示待选课程总数(1≤M≤1000),N表示学生可以选的课程总数(1≤N≤M)。 以下M行每行代表一门课,课号依次为1,2……M。每行有两个数(用一个空格隔开),第一个数为这门课的先修课的课号(若不存在先修课则该项为0),第二个数为这门课的学分。学分是不超过10的正整数。 输出 输出文件第一行只有一个数,即实际所选课程的学分总数。以下N行每行有一个数,表示学生所选课程的课号。 二、分析 本题看上去不太好动手。这是一道求最优解的问题,如果用搜索解题,那规模未免过于庞大;用动态规划,本题数据之间的关系是树形,和我们往常见到线性的数据关系不一样。 怎么办?我们先从一些简单的数据入手分析。如表1所示的输入数据,我们可将它看为由两棵树组成的森林,如图1所示。 我们发现,我们可以选取某一个点k的条件只是它的父节点已经被选取或者它自己为根节点;而且我们不论如何取k的子孙节点,都不会影响到它父节点的选取情况,这满足无后效性原则。于是我们猜测,是不是可以以节点为阶段,进行动态规划呢? 我们用函数f(I,j)表示以第i个节点为父节点,取j个子节点的最佳代价,则: 可是如此规划,其效率与搜索毫无差别,虽然我们可以再次用动态规划来使它的复杂度变为平方级,但显得过于麻烦。 我们继续将树改造:原本是多叉树,我们将它转变为二叉树。如果两节点a,b同为兄弟,则将b设为a的右节点;如果节点b是节点a的儿子,则将节点b设为节点a的左节点。树改造完成后如图3。 我们用函数f(I,j)表示以第i个节点为父节点,取j个子节点的最佳代价,这和前一个函数表示的意义是一致的,但方程有了很大的改变: 这个方程的时间复杂度最大为n3,算十分优秀了。 在具体实现这道题时,我们可以自顶而下,用递归进行树的遍历求解;在空间方面,必须特别注意。因为如果保存每一个f(I,j),bp下是不可能的。我们必须用多少开多少,这样刚好可以过关。(具体请参见程序) 分析(自) 很容易想到在树上背包来解决问题,假设f[i][j]为以i为根的子树,包括i,选择j门课的最大值 那么有f[i][j]=max{ f[i][a]+f[k][b] }k是i的子树,a+b=j 这样的复杂度是O(n*m^2)对于这题的数据范围来说还是够用的,不过我用上了对这种泛化物品的背包的一种优化复杂度降为O(n*m) 砝码称重(noip’96) 一、 问题描述 设有1g、2g、3g、5g、10g、20g的砝码各若干枚(其总重<=1000),用他们能称出的重量的种类数。 输入:a1 a2 a3 a4 a5 a6表示1g砝码有a1个,2g砝码有a2个,…,20g砝码有a6个,中间有空格)。 输出:Total=N(N表示用这些砝码能称出的不同重量的个数,但不包括一个砝码也不用的情况)。 样例输入 1 1 0 0 0 0 样例输出 3 二、分析 就是个01背包……f[0]:=true把问题稍做一个改动,已知a1+a2+a3+a4+a5+a6个砝码的重量w[i], w[i]∈{ 1,2,3,5,10,20} 其中砝码重量可以相等,求用这些砝码可称出的不同重量的个数。这样一改就是经典的0/1背包问题的简化版了,求解方法完全和上面说的一样 设dp[1000]数组为标记数组。当dp[i]=0时,表示质量为i的情况,目前没有称出;当dp[i]=1时,表示质量为i的情况已经称出。题目中有多个砝码,我们顺序处理每一个砝码。当处理第j个砝码,质量为wj时,有下列推导公式: d[i-wj]=1==>d[i]=1(当且仅当质量i-wj已经称出,才能称出质量i) 核电站问题 一、题目描述 一个核电站有N个放核物质的坑,坑排列在一条直线上。如果连续M个坑中放入核物质,则会发生爆炸,于是,在某些坑中可能不放核物质。 现在,请你计算:对于给定的N和M,求不发生爆炸的放置核物质的方案总数。 二、分析 法1:设f[i]为第i个位置不爆炸的方案数,注意!这个f一定是合法的!则这个位置可以放/不放,(别急,不一定合法~)f[i-1]*2但不能连续放m个,所以>=m时需要减去保证只连了m个,即前m-1全放了,而i-m(绿圈)一定不放 的 1种情况 ----f[i-m-1]<---(合法的) 不管它是如何组成的,这是dp的精髓正对的头是i-m+1 而初始值f[0]=1有意义,第0个就是不放。但f[-1]是由 推f[m]=f[m-1]*2-f[i(m)-m-1]为了正解,设的f[-1]=1 数的划分(noip2001) 一、问题描述 将整数n分成k份,且每份不能为空,任意两份不能相同(不考虑顺序)。 例如:n=7,k=3,下面三种分法被认为是相同的。 1,1,5; 1,5,1; 5,1,1; 问有多少种不同的分法。 输入:n,k(6 输出不同分法 例如:7 3 输出4 分析:用f(I,j)表示将整数I分成j分的分法,可以划分为两类: 第一类 :j分中不包含1的分法,为保证每份都>=2,可以先那出j个1分到每一份,然后再把剩下的I-j分成j份即可,分法有:f(I-j,j). 第二类 : j份中至少有一份为1的分法,可以先那出一个1作为单独的1份,剩下的I-1再分成j-1份即可,分法有:f(I-1,j-1). 所以:f(I,j)=f(I-j,j)+ f(I-1,j-1) 最大01矩阵 一、题目描述 给定一个n*m的01矩阵 11111 10001 11111 答案:15 Your Task:求出面积最大的0类矩形的面积s 输入:第一行两个数n、m。接下来n行每行m个数。n <= 2000,m <= 2000 输出:每行一个数s 二、分析 本题中符合要求的矩形可以分为2种: 1.1*k和2*k 2.k1 * k2的 对于第一种,由于这种矩形全部是由1构成的,扫描一次更新答案就可以了。 对于第二种,注意到里面那层0构成0的一个极大联通块。因此,我们只用找出每一个0的极大联通块,然后判断是否是题目要求的图形就可以了。 在判断的时候,只用注意3个地方: 1.是否有0延伸到了矩阵的边缘,有的话显然不符合要求 2.这个联通块是否构成一个矩形。构不成矩形显然也不行。 3.周围的1是否能构成一个完整的壳。 具体实现的时候,可以记录这个极大联通块所能延伸到最远的行列。即程序中的max_row,min_row,max_column,min_column。以及当前块的面积sum. 然后对1,只用判断是这四个值是否等于对应的边界。 对于2,只用判断又这四个行列所确定的矩形面积是否等于sum。 对于3,只用判断加上1之后的大矩形四个角是为1,因为边是一定全部为1的。 这样,就可以在O(mn)的时间内解决本题了。 最大子矩阵(Scoi’05) 一、问题描述 这里有一个n*m的矩阵,请你选出其中k个子矩阵,使得这个k个子矩阵分值之和 最大。注意:选出的k个子矩阵不能相互重叠。 输入格式:第一行为n,m,k(1≤n≤100,1≤m≤2,1≤k≤10),接下来n行描述矩阵每行中的每个元素的分值(每个元素的分值的绝对值不超过32767)。 输出格式:只有一行为k个子矩阵分值之和最大为多少 样例输入: 3 2 2 1 -3 2 3 -2 3 输出:9 二、分析 由于m<=2可以分情况讨论 (1)m = 1 时就相当于1维,用g[i][j]表示前i个数字选出j段的最大分值转移是O(N)的,往前枚举即可 (2)m = 2时f[i][j][k]表示第一列前i个数字,第二列前j个数字选出k个子矩阵的最大分值转移还是O(N) f[i][j][k] =max(f[i - 1][j][k], f[i][j - 1][k]); f[i][j][k] =max{ f[i][j][k], f[x][j][k - 1] + s1[i] - s1[x] }; f[i][j][k] =max{ f[i][j][k], f[i][y][k - 1] + s2[j] - s2[y] }; 当 i = j 时 f[i][j][k] = max{ f[i][j][k], f[x][x][k - 1] + s1[i] - s1[x] +s2[i] - s2[x] } 如果是 2*n 的话用 a1 表示第一行的个数,a2表示第二行,k表示选出矩阵个数DP情况是靠最后一个矩阵是否在边界上。如果a1 != a2 那么dp(k,a1,a2) = max(dp(k,a1-1,a2),dp(k,a1,a2-1),dp(k-1,a1-j,a2)+ value(第k矩阵),dp(k-1,a1,a2-j) +value(第k矩阵)),a1 == a2,那么就有可能是最后一个矩阵是一个2*j的矩阵。那么就还有可能最大的是这种情况那么就加dp(k,a1,a2) = max(dp(k,a1,a2),dp(k-1,a1-j,a2-j) + value(第k矩阵)) 加+-被k整除(poj1745) 一、题目描述:n个整数中间填上+或者-,运算结果能否被k整除。1<=n<=10000,2<=k<=100 二、分析:已知(a+b)%m =(a%m + b%m)%m;那么f[i,j] 表示 前i个数运算结果mod k是否存在余数j,转移方程就简单了:如果f( i-1, j)为true,那么把f(i,(j+a[i])mod k)和f(i, (j-a[i])mod k)置真。由于可能会出现复数的情况,处理可以要么把数组开到负的,要么加一个很大的k的倍数再mod。要么特判 方块消除(poj1390) 一、问题描述:一款叫做方块消除的游戏。游戏规则如下:n个带颜色方格排成一列,相同颜色的方块连成一个区域(如果两个相邻方块颜色相同,则这两个方块属于同一区域。游戏时,你可以任选一个区域消去。设这个区域包含的方块数为x,则将得到x^2个分值。方块消去之后,其余的方块就会竖直落到底部或其他方块上。而且当有一列方块被完全消去时,其右边的所有方块就会向左移一格。虽然游戏很简单,但是要拿高分也很不容易。找出得最高分的最佳方案 输入格式:第一行包含一个整数n(0<=n<=100),表示方块数目。第二行包含n个数,表示每个方块的颜色(1到n之间的整数)。 输出格式:仅一个整数,即最高可能得分。 二、分析 /*设计状态f[i,j,k]表示[i..j]段序列和后面的k个方块消去所得到的最大值。说明: 后面的k个方块是火星来的咩?肯定不是...是后面的某个区间有k个方块,暂且称之为late。此区间的颜色和j区间相同。消掉了j和late区间中间的方块,于是j区间和late区间就连在一起了,并且消掉[j+1..late-1]的这一块的值是在上一步子问题中解决的,在这一个子问题中体现不出来。 刚开始看别人的解释也是一头雾水,后来看了程序就明白了。 子问题是一段区间的序列怎么消,和别人一起消,还是自己消了算了。 len[late]=k;colour[j]=colour[late];现在late和j紧挨在一起,可以算是一个区间了。 状态转移: f[i,j,k]:=f[i,j-1,0]+(len[j]+k)^2;如果现在就将j和late的和区间消掉。 f[i,j,k]:=f[i,p,len[j]+k]+f[p+1,j-1,0];(colour[p]=colour[j]=colour[late])如果j和late再和前面的某一区间合并后再消掉。从这里也可以看出为什么求解f[i,p,len[j]+k]这一个子问题的时候没有求到f[p+1,j-1,0]这一部分,这解释了上一部分中的斜体字部分。 f[i,j,k]:=(len[i]+k)*(len[i]+k);(i=j); 用f [ i ] [ j ] [ k] 表示把(color [ i ] , len [ i ] ), (color [ i+1 ] , len [ i+1 ] ) ,……, (color [j-1 ] , len [ j-1 ] ),(color [j ] , len [ j ]+k )合并的最大得分 考虑(color [ j ] ,len [ j ]+k )这一段要不马上消去 要不和前面的一起消去 如果马上消去:f【i】【j-1】【0】+(len【j】+k)^2 如果和前面一起消去 那么前面有的段数可以有P位 那么得分可以有P种情况 f【i】【p】【k+len[j]】+f【p+1】【j-1】【0】;(color【p】=color【j】 i<=p 所以f 【i】【j】【k】=两个的最大值. 边界条件是f【i】【i-1】【0】=0*/ 装箱问题(noip2001) 一、问题描述:有一个箱子容量为V(正整数,0<=V<=20000),同时有n个物品(0<n<=30=,每个物品有一个体积(正整数)。要求n个物品中,任取若干个装入箱内,使箱子的剩余空间为最小。 二、分析:首先,对于第I个背包,有选与不选两种状态。我们设F[i]表示使用容量为i的背包所获得的最大价值,则F[i]:=Max(F[i-w[i]]+a[i],F[i])这个状态转移方程 数字三角形 示出了一个数字三角形。 请编一个程序计算从顶至底的某处的一条路径,使该路径所经过的数字的总和最大。每一步可沿左斜线向下或右斜线向下走;1<三角形行数<25; 三角形中的数字为整数<1000; 晴天小猪历险记同一阶段上暴力动态规划 一、问题描述:晴天小猪来到了一座深山的山脚下,因为只有这座深山中的一位隐者才知道这种药草的所在。但是上山的路错综复杂,由于小小猪的病情,晴天小猪想找一条需时最少的路到达山顶,山用一个三角形表示,从山顶依次向下有1段、2段、3段等山路,每一段用一个数字T(1<=T<=100)表示,代表晴天小猪在这一段山路上需要爬的时间,每一次它都可以朝左、右、左上、右上四个方向走(注意:在任意一层的第一段也可以走到本层的最后一段或上一层的最后一段)。晴天小猪从山的左下角出发,目的地为山顶,即隐者的小屋。 输入格式:第一行有一个数n(2<=n<=1000),表示山的高度。从第二行至第n+1行,第i+1行有i个数,每个数表示晴天小猪在这一段山路上需要爬的时间。 输出格式:一个数,即晴天小猪所需要的最短时间。 输入 5 1 2 3 4 5 6 10 1 7 8 1 1 4 5 6 输出:10 二、分析 DP数字三角形的一个扩展,一道好题。可得dp方程 f[i,j]=min{f[i-1,j-1],f[i-1,j],f[i,j-1],f[i,j+1]}+a[i,j] 边缘的走法: (5, 1)能走到(5, 5)(5, 2)(4, 1)(4, 4) (5, 5)能走到(5, 1)(5, 4)(4, 1)(4, 4) 重诉一下题目的意思,第一小猪走的方向有四个左上,右上,左,右,在任意一层的第一段也可以走到本层的最后一段或上一层的最后一段,而最后一段也可以走到第一段。找从左下角走到山顶的最少时间。第二数据给出的是圆锥形的。 1 2 3 4 5 6 9 1 7 8 1 1 4 5 6 与数字三角形不同的地方就是可以左,右走,在任意一层的第一段也可以走到本层的最后一段或上一层的最后一段,而最后一段也可以走到第一段。第一段和最后一段的特殊性可以单独判断,重点在于如何去掉左右走的后效性,和找出当前的最小值。这里说一种简单的方法,网上大多数的人都用这种方法也做这道题。就是先进 行左上和右上的操作这样就一定有一个已经确定了的最小值,它在左,右操作都不会被改变,因为下面一层已经计算出最优值,它一定是由那下面直接走上来的。然后由这个点去改变其他点,然后判断出第一个和最后一个的值,是否可以再次被改变。再从头到尾循环一次,从尾到头循环一次,这样就可以计算出当前一层的最优 值,这样一值做到第一层。 网上的题解: 1.DP有环怎么办? 别急,先别想着放弃DP,有时候环是可以避免的.这里在每一行中为避免相邻两格左右移动产生的环,可以先推向左的,再推向右的,而同向移动产生的那个“大”环就麻烦一点.其实有个很简单的窍门:先记录从下一行转移来的最优值,然后在本行中寻找代价最小的点,以这个点为起点分别向左向右推,因为最小的点 显然是不需要从两侧的点过来的.这样就没有后效性了.. 2.递推的顺序: 递推有两种顺序,可以根据当前状态值推出所有可能的后继状态,也可以根据所有当前状态可能的前驱来推当前值,很多时候,当问题的状态比较有规律时,这两种 方法是不相上下的.但是其他情况下一不小心就可能搞错.比如这题题目告诉我们的是从一个状态可行的所有走法(共四种),所以根据这个顺序去编是最保险的。 因为这里一个状态的前驱不一定只是四个,边缘的点是特例,可能会有5个来源,所以DP的时候不要随便换状态转移顺序. 这道题还可以用最短路经算法来做,把两个可以走的点看成一条边。 对于程序,可以自己画个图 小胖办证(双向动态规划1,数字三角形) 问题描述:xuzhenyi要办个签证。办证处是一座M层的大楼,1<=M<=100。每层楼都有N个办公室,编号为1..N(1<=N<=500)。每个办公室有一个签证员。签证需要让第M层的某个签证员盖章才有效。每个签证员都要满足下面三个条件之一才会给xuzhenyi盖章: 1. 这个签证员在1楼 2. xuzhenyi的签证已经给这个签证员的正楼下(房间号相同)的签证员盖过章了。 3. xuzhenyi的签证已经给这个签证员的相邻房间(房间号相差1,楼层相同)的签证员盖过章了。 每个签证员盖章都要收取一定费用,这个费用不超过1000000000。找出费用最小的盖章路线,使签证生效 二、分析 DP顺序:从下到上,再从左到右,再从右到左,与上题一样,为了保证其无后效性,所以同一层的需要分开扫描 坐标型DP。设计一个状态f[i,j]为找第i层第j个签证员所要花费的总费用。 状态转移很明显。 f[i,j]:=min{f[i-1,j]+a[i,j];f[i,j-1]+a[i,j];f[i,j+1]+a[i,j];} 只是f[i,j-1]和f[i,j+1]不能够在同一次循环中全部求出来,所以要扫两次。 记录路径:用x和y分别记录 马拦卒过河noip2002 一、问题描述:棋盘上A点有一个过河卒,需要走到目标B点。卒行走的规则:可以向下、或者向右。同时在棋盘上C点有一个对方的马,该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。棋盘用坐标表示,A点(0, 0)、B点(n, m)(n, m为不超过15的整数),同样马的位置坐标是需要给出的。现在要求你计算出卒从A点能够到达B点的路径的条数,假设马的位置是固定不动的,并不是卒走一步马走一步。 二、分析:就是简单考虑路径,但是这里需要注意的一个是马的地方不能走,这个特判下就好了,还有就是边界条件,如果马走了边界,那么边界要注意赋值为前一个 打砖块(tyvj’1505) 一、 问题描述: 在一个凹槽中放置了n层砖块、最上面的一层有n 块砖,从上到下每层依次减少一块砖。每块砖都有一个分值,敲掉这块砖就能得到相应的分值,如下图所示。 14 15 4 3 23 33 33 76 2 2 13 11 22 23 31 如果你想敲掉第i层的第j块砖的话,若i=1,你可以直接敲掉它;若i>1,则你必须先敲掉第i-1层的第j和第j+1块砖。 你现在可以敲掉最多m块砖,求得分最多能有多少。 二分析: f[i,j,k]表示,到了第i行,总共取j个,在第i行取k个用g[i,j,k]数组记录从f[i,j,k]到f[i,j,i]中的最大值,用s[i,j]记录转换后的第i行前j个数的和 方程:f[i,j,k]=g[i-1,j-k,k-1]+s[i,k]; 把三角形倒过来了! 比如说样例: 2 2 3 4 8 2 7 2 3 49 倒过来之后——> 4 3 7 2 2 3 2 8 2 49 那么每一点只能由左边的点转移过来,和左上角一直到上一行末尾的数转移过来。 如第四行第2个数可以从第三行的1,2,3个数转移过来。为什么?再回去看看题吧…… 此题就是典型的区间DP,先搬砖块都变成直角三角形,然后分析阶段和边界,通过题里的叙述很容易推出递推公式:f[i][j][k]=f[i][j][k]+a[v][i]; 边界:f[n+1][0][0]=0; 目标:f[i][j][k]; 从右向左推,f[i,j,k]表示第i列敲掉j个砖头一共敲掉k个砖头所得到的最优值。第i列敲掉j个砖头,则第i+1列就至少要敲掉j-1个砖头。第i列一共要敲掉k个,第i+1列及其以前就要敲掉k-j个砖头。 f[i,j,k]:=max(f[i+1,v,k-j])+sum[j,i];(j-1<=v<=n-i) sum[j,i]表示第i列,从第1行到第j行所有砖头的值的和 注意边界条件,赋初值要赋一个很大的负数。然后把f[n+1,0,0]赋成0 0<=j<=n-i+1,j<=k<=m 注意:j应该从0开始,而不能从1开始,因为该列可以一个也不取,而这个状态应该被保存,否则不一定达到最优。 打鼹鼠(CscIIvijos 1441) 一、问题描述:阿Q编写了一个打鼹鼠的游戏:在一个n*n的网格中,在某些时刻鼹鼠会在某一个网格探出头来透透气。你可以控制一个机器人来打鼹鼠,如果i时刻鼹鼠在某个网格中出现,而机器人也处于同一网格的话,那么这个鼹鼠就会被机器人打死。而机器人每一时刻只能够移动一格或停留在原地不动。机器人的移动是指从当前所处的网格移向相邻的网格,即从坐标为(i,j)的网格移向(i-1, j),(i+1, j),(i,j-1),(i,j+1)四个网格,机器人不能走出整个n*n的网格。游戏开始时,你可以自由选定机器人的初始位置。现在你知道在一段时间内,鼹鼠出现的时间和地点,希望你编写一个程序使机器人在这一段时间内打死尽可能多的鼹鼠。 输入格式:文件第一行为n(n<=1000), m(m<=10000),其中m表示在这一段时间内出现的鼹鼠的个数,接下来的m行每行有三个数据time,x,y表示有一只鼹鼠在游戏开始后time个时刻,在第x行第y个网格里出现了一只鼹鼠。Time按递增的顺序给出。注意同一时刻可能出现多只鼹鼠,但同一时刻同一地点只可能出现多只鼹鼠。 输出格式:输出文件中仅包含一个正整数,表示被打死鼹鼠的最大数目。 二、分析:分析:经典DP题。这题一开始很容易想到一个(n^2t)的算法,定义dp[i][j][k]表示在第i秒,站在点(j,k)上所能打到的最多鼹鼠数目,方程也很好列。可惜n最多要有1000,而且k也不小,使用这个方法必定超时+超内存。仔细分析此题,发现假如机器人要移动到某个位置,那么它一定是走一条最短路径(其实就是曼哈顿距离,公式distance=|x1-x2|+|y1-y2|)否则解就不一定是最优的。还有,假如在某个点打死了一个地鼠,那么机器人的位置一定是站在那个死掉地鼠出现的位置上。这样我们就可以想出一个新的状态表示方法:定义dp[i]表示对于前i只鼹鼠,最多能打死多少只,而且当前机器人站在i号鼹鼠的位置。这样方程就类似于LCS问题,也就是对于当前的鼹鼠位置,枚举机器人上一次打死鼹鼠的地方,判断这两个地方是否可以到达,如果可以到达那么dp[i]+1,否则continue。 这里有一个小优化:在枚举鼹鼠位置的时候可以倒着枚举,这样简单的常数优化居然提高了1.2s的程序运行速度! 贪吃的九头龙(NOI2002) 一、问题描述:传说中的九头龙是一种特别贪吃的动物。虽然名字叫“九头龙”,但这只是说它出生的时候有九个头,而在成长的过程中,它有时会长出很多的新头,头的总数会远大于九,当然也会有旧头因衰老而自己脱落。 有一天,有M个脑袋的九头龙看到一棵长有N个果子的果树,喜出望外,恨不得一口把它全部吃掉。可是必须照顾到每个头,因此它需要把N个果子分成M组,每组至少有一个果子,让每个头吃一组。 这M个脑袋中有一个最大,称为“大头”,是众头之首,它要吃掉恰好K个果子,而且K个果子中理所当然地应该包括唯一的一个最大的果子。果子由N-1根树枝连接起来,由于果树是一个整体,因此可以从任意一个果子出发沿着树枝“走到”任何一个其他的果子。 对于每段树枝,如果它所连接的两个果子需要由不同的头来吃掉,那么两个头会共同把树枝弄断而把果子分开;如果这两个果子是由同一个头来吃掉,那么这个头会懒得把它弄断而直接把果子连同树枝一起吃掉。当然,吃树枝并不是很舒服的,因此每段树枝都有一个吃下去的“难受值”,而九头龙的难受值就是所有头吃掉的树枝的“难受值”之和。 九头龙希望它的“难受值”尽量小,你能帮它算算吗? 二、分析 题目简述:将一棵树中的节点染成M种颜色,每个节点有且只有一种颜色,在满足以下条件下使得两端颜色相同的边的权值和最小,所有边权均非负。(1)必须有K个1号颜色的点;(2)1号节点必须是1号颜色;(3)每种颜色必须至少有一个节点。如无解,输-1。 无解的情况很明显,当且仅当N-K 如果以一棵子树作为一个子结构,分析需要考虑的状态: (1)根节点的颜色。(2)1号颜色的个数。(3)树中颜色的分配情况,如何保证每种颜色都有节点。 初步分析可以得到一种四维的状态: f[i][j][k][w],表示在以i为根的子树中,有j个1号节点,根染k号颜色,树中已有的颜色用w表示(w是一个二进制数)的状态下最小的权值和。 首先,这个方程用到了状态压缩w,因此对于本题300的数据范围是不现实的,需要继续思考。 假设这样一个问题,仍然是对树染色,可以任意染色,那么只要2种颜色,就可以保证任意一条边两端的颜色不同,联想到这道题,因为1号颜色比较特殊,因此单独处理,而余下的颜色如果大于等于2种,那么无论1号颜色如何染色,都可以保证一条边两边不会出现相同的非1号颜色的情况,换言之,如果M>=3,对答案有贡献的只有1号颜色节点之间的边。这样当M>=3时,可以直接按3处理,这样状态压缩是可以承受的。既然有了这样的优化,k也可以只用0,1来表示,1表示1号颜色,0表示非1号颜色。而M=2时就更简单了,0,1就直接把颜色分开了。 初步分析下来,得到了一个状态数为O(N*K*2*2³),转移为O(K*2*2³),总复杂度为O(N*K²*256)。由于N,K≤300,理论分析是会超时,但实际操作中可以不用循环到K,因为循环的上限可以设为min(K,子树i的总节点数)。这样的话,这个复杂度还是可以承受的。 本题还有优化吗?答案是肯定的。 如果要优化状态,前3维似乎是无法优化的,考虑第4维。之所以一开始要加入这一维,就是担心会存在有一些颜色无法染上的问题,经过后来的分析,发现除了1号颜色会对答案有贡献之外,其他颜色其实是可以被忽略的,因为我们可以保证它们不会对答案造成影响,那么只要有足够多的节点来染除1外的颜色,就可以确保每一种颜色都可以被染上,至于到底在哪里,其实并不重要。这样想,就会发现其实第四维是完全多余的,可以直接略去。 最终状态:f[i][j][k], 表示在以i为根的子树中,有j个1号节点,根染k号颜色的状态下最小的权值和。 如果能把M个脑袋简化成一个脑袋吃K个的最小代价就好了。想一想其实可以分两种情况: 1、M=2,就是大头吃掉的树枝+小头吃掉的树枝。 2、M>2,此时只需考虑大头吃掉的树枝,因为其他的可以根据奇偶分给不同的头吃,从而使他们不被算入最终答案。 然后就是一个简单的树形DP题,先把树转成二叉树, 然后:f[i][j][k]=min{f[lc[i]][X][0]+f[rc[i]][j-X][k]+(m==2)*(k==0)*d[i]|| f[lc[i]][X-1][1]+f[rc[i]][j-X][k]+(k==1)*d[i]} f[i][j][k]指以i为根的子树分j个给大头吃,父亲是k(k=1被大头吃k=0被小头吃)。 状态压缩dp炮兵阵地(poj1185) 一、问题描述:司令部的将军们打算在N*M的网格地图上部署他们的炮兵部队。一个N*M的地图由N行M列组成,地图的每一格可能是山地(用“H” 表示),也可能是平原(用“P”表示),如下图。在每一格平原地形上最多可以布置一支炮兵部队(山地上不能够部署炮兵部队);一支炮兵部队在地图上的攻击范围如图中黑色区域所示: 如果在地图中的灰色所标识的平原上部署一支炮兵部队,则图中的黑色的网格表示它能够攻击到的区域:沿横向左右各两格,沿纵向上下各两格。 图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。 现在,将军们规划如何部署炮兵部队,在防止误伤的前提下(保证任何两支炮兵部队之间不能互相攻击,即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内),在整个地图区域内最多能够摆放多少我军的炮兵部队。 二、分析:1. 为何状态压缩: 棋盘规模为n*m,且m≤10,如果用一个int表示一行上棋子的状态,足以表示m≤10所要求的范围。故想到用ints[num]。至于开多大的数组,可以自己用DFS搜索试试看;也可以遍历0~2^m-1,对每个数值的二进制表示进行检查;也可以用数学方法 2. 如何构造状态: 当然,在此之前首先要想到用DP(?)。之后,才考虑去构造状态函数f(...)。 这里有一个链式的限制 :某行上的某个棋子的攻击范围是2。即,第r行的状态s[i],决定第r-1行只能取部分状态s[p];同时,第r行的状态s[i],第r-1行状态s[p],共同决定第r-2行只能取更少的状态s[q]。当然,最后对上面得到的候选s[i], s[p], s[q],还要用地形的限制去筛选一下即可。 简言之,第r行的威震第r-2行,因此在递推公式(左边=右边)中,必然同时出现r,和r-2两个行标;由于递推公式中行标是连续出现的,故在递推公式中必然同时出现r, r-1和r-2三个行标。由于在递推公式中左边包含一个f(...),右边包含另一个f(...),根据抽屉原理,r, r-1, r-2中至少有两个在同一个f(...)中,因此状态函数中必然至少包括相邻两行的行号作为两个维度。这就是为什么状态函数要涉及到两(相邻的)行,而不是一行。能想到的最简单形式如下: dp[r][i][p]:第r行状态为s[i],第r-1行状态为s[p],此时从第0行~第r行棋子的最大数目为dp[r][i][p] 滚动数组版本: //明白该题核心算法之后,可以进一步优化,使用滚动数组。其依据为炮兵攻击范围上下2行,所以 //任意行只与其相邻的两行相互影响,所以创建一个f[2][61][61]的滚动数据即可求解。 //用滚动数组依次求出每行的最优解 常用递推式子 递推天地-----情书抄写员矩阵连乘(斐波那契) f[i]:=f[i-1]+k*f[i-2] 递推天地-----错位排列的递推式 f[i]:=(i-1)(f[i-2]+f[i-1]); f[n]:=n*f[n-1]+(-1)^(n-2); 递推天地-----凸多边形分三角形方法数(卡特兰数的应用) f[n]:=C(2*n-2,n-1)div n; 对于k边形 f[k]:=C(2*k-4,k-2)div (k-1); //(k>=3) 递推天地-----Catalan数列一般形式 f[n]:=C(2k,k)div (k+1); 卡特兰数的应用 http://blog.csdn.net/yushuai007008/article/details/7693405 http://blog.163.com/lz_666888/blog/static/1147857262009914112922803/ 1、 括号化问题 P=a1*a2*a3*…*an,依据乘法结合律,不改变其顺序,只用括号表示成对的乘积,试问有几种括号化的方法。 解:设P(n)表示n个元素括号化的数目。如果a1前的左括号和ai后的右括号相匹配,那么a1…ai括号化的数目为P(i),a(i+1)…an括号化的数目为P(n-i).此时括号化的数目为P(i)*P(n-i)。 a1…an括号化数目:P(n)=P(1)*P(n-1)+P(2)*P(n-2)+…+P(i)*P(n-i)+…+ P(n-1)*P(1)。 下面来证明P(n)=h(n-1) 1)P(1)=h(0)=1,P(2)=h(1)=1 2)设P(m)=h(m-1),对于m=1,2,…,n-1成立 P(n)=∑P(k)*P(n-k) (其中,k=1,2,。。。。,n-1)=∑h(k-1)*h(n-k-1) 设t=k-1 =∑h(t)*h(n-t-2)(其中,t=0,1,。。。,n-2) =h(n-1) 所以,n个元素括号化的数目是h(n-1)。n个矩阵链的一个括号化,与具有n-1个内节点n个叶节点的分析树相对应。 2、 有n个节点的二叉树共有多少种情形? 解:有h(n)种情形 自己的理解: 一共有a0,a1,a2,…,an共n个元素,由它们来构造二叉树。h(n)表示这n个元素一共可以构成h(n)个不同的二叉树。如果选取a0作为根节点,那么其左子树包含0个元素,左子树的数目是h(0);其右子树包含n-1个元素,右子树的数目是h(n-1);以a0为根节点的二叉树的数目是h(0)*h(n-1)。如果选取a1作为根节点,那么其左子树包含1个元素a0,左子树的数目是h(1);其右子树包含h(n-2)个元素,右子树的数目是h(n-2);以a1为根节点的二叉树的数目是h(1)*h(n-2)。如果选取ai作为根节点,其左子树包含i个元素,左子树的数目是h(i);右子树包含n-i-1个元素,右子树数目为h(n-i-1);以ai为根节的二叉树的数目是h(i)*h(n-1-i)。 总的二叉树的数目为h(n)=h(0)*h(n-1)+h(1)*h(n-2)+…+h(i)*h(n-1-i)+…+h(n-1)*h(0) 如果一共有0个节点,那么二叉树的数目为h(0)=1;如果一共有1个节点,那么二叉树的数目为h(1)=1 3、 出栈次序问题 一个栈(无穷大)的进栈序列为1,2,3,…,n,有多少个不同的出栈序列? 对于每个数,必须入栈一次,出栈一次。把入栈设为状态1,出栈设为状态0。n个数的所有状态对应于n个1和n个0组成的2n位二进制数。由于等待入栈的操作数按照1。。。n的顺序入栈,入栈的次数一定大于等于出栈的次数。因此,合法的输出序列是满足下面条件的序列:由左向右扫描由n个1和n个0组成的2n位二进制数,1的累计数不小于0的累计数。 解法1:第0个符号一定是1,否则该序列不合法。假设第0个1和第k个0相匹配,那么从第1个符号到第k-1个符号,从第k+1个符号到第n-1个符号也都是一个合法的序列。可以知道,k一定是一个奇数,设k=2*i+1(i=0,1,2,…,n-1) 假设2n个符号中合法的序列数为f(2n),则f(2n)= ∑f(2i)*f(2n-2*i-2),其中,i=0,1,…,n-1。 下面证明f(2n)=h(n) 1)f(0)=h(0)=1,f(2)=h(1)=1 2)假设当对于小于等于n的任意整数m满足:f(2m)=h(m) f(2n)= ∑f(2i)*f(2n-2*i-2),其中,i=0,1,…,n-1 =∑h(i)*h(n-i-1),其中,i=0,1,…,n-1 =h(n) 所以,1,2,…,n,共有h(n)种不同的出栈序列.由n个0和n个1组成的满足下面条件的序列总数为h(n):1的个数不小于0的个数。 解法2:证明每个不合法序列与n+1个0和n-1个1组成的序列是一一对应的 不合法的序列从左向右扫描时,必然存在某一位上首先出现m+1个0和m个1(如果第0位是0,那么第0位就是满足条件的为。如果第0位是1,那么第0位上1的个数比0的个数多1,同时因为序列不合法,必然存在某一位上0的个数比1的个数多;所以,一定存在某一位上出现1的个数比0的个数少1)。此后的2n-2m-1位上有n-m个1和n-m-1个0。如果把后边的2n-2m-1位上的0和1互换,使之成为含有n-m个0和n-m-1个1的序列,结果得由n+1个0和n-1个1组成的序列。 反过来,任何一个由n+1个0和n-1个1组成的序列。因为0的个数比1的个数多2,所以必在某一位上出现0的个数比1的个数多1。同样在后面部分0和1互换,使之成为由n个0和n个1组成的序列,即n+1个0和n-1个1组成的序列对应一个不合法的序列。 因此,不合法的2n个数的序列与由n+1个0和n-1个1组成的序列一一对应。 显然,不合法的方案数位C(2n,n-1),由此得出合法的序列数为C(2n,n) -C(2n,n+1)=C(2n,n)/(n+1)。 4、买票找零问题 球票为50元,有2n个人排除买票,其中n个人手持50元的钞票,n个人持100元的钞票,假设售票处无零钱,问这2n个人有多少种排列方式,不至于使售票处出现找不开钱的局面。 解:h(n)。 5、凸多边形的三角剖分问题 求将一个凸多边形区域分成三角形区域的方法数。 对于有n条边(n+1个顶点)的多边形的一个三角剖分与具有n-1个叶节点的分析树对应。所以,由n+1个顶点n条边构成多边形的三角剖分数目为h(n-2). 公式:f(n)=f(2)f(n-2+1)+f(3)f(n-3+1)+……+f(n-1)f(2)。 f(2) = 1 , f(3) = 1,f(4)=2,f(5)=5,f(6)=14 ………… 6、上班路径问题 一位律师在住所以北n个街区和以东n个街区工作。每天她走2n个街区去上班。如果她不穿越(但可以碰到)从家到办公室的对角线,那么有多少条可能的道路? 解:h(n) 7、圆上的点连线问题 在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数? 解:h(n) (1) n条直线最多分平面问题 题目大致如:n条直线,最多可以把平面分为多少个区域。 f(n)=f(n-1)+n==>n(n+1)/2+1 (2) 折线分平面(hdu2050) 根据直线分平面可知,由交点决定了射线和线段的条数,进而决定了新增的区域数。当n-1条折线时,区域数为f(n-1)。为了使增加的区域最多,则折线的两边的线段要和n-1条折线的边,即2*(n-1)条线段相交。那么新增的线段数为4*(n-1),射线数为2。但要注意的是,折线本身相邻的两线段只能增加一个区域。 f(n)=f(n-1)+4(n-1)+2-1==>2n^2-n+1 (3) 封闭曲线分平面问题 题目大致如设有n条封闭曲线画在平面上,而任何两条封闭曲线恰好相交于两点,且任何三条封闭曲线不相交于同一点,问这些封闭曲线把平面分割成的区域个数。 析:当n-1个圆时,区域数为f(n-1).那么第n个圆就必须与前n-1个圆相交,则第n个圆被分为2(n-1)段线段,增加了2(n-1)个区域。 f(n)=f(n-1)+2(n-1)==>n^2-n+2 (4)平面分割空间问题(hdu1290) 由二维的分割问题可知,平面分割与线之间的交点有关,即交点决定射线和线段的条数,从而决定新增的区域数。试想在三维中则是否与平面的交线有关呢?当有n-1个平面时,分割的空间数为f(n-1)。要有最多的空间数,则第n个平面需与前n-1个平面相交,且不能有共同的交线。即最多有n-1 条交线。而这n-1条交线把第n个平面最多分割成g(n-1)个区域。(g(n)为(1)中的直线分平面的个数)此平面将原有的空间一分为二,则最多增加g(n-1)个空间。 故:f(n)=f(n-1)+g(n-1)==>(n^3+5n)/6+1 ps:g(n)=n(n+1)/2+1 排列组合中的环形染色问题 一个环形的花坛(不包括中心,中心可能建喷泉 - -!)分成n块,然后有m种颜色的花可供选取,要求相邻区域颜色不能相同,共有多少种方法 隐形的翅膀-线性搜索 天使告诉小杉,每只翅膀都有长度,两只翅膀的长度之比越接近黄金分割比例,就越完美。现在天使给了小杉N只翅膀,小杉想挑出一对最完美的。 输入格式:每组测试数据的 第一行有一个数N(2<=N<=30000) 第二行有N个不超过1e5的正整数,表示N只翅膀的长度。 20%的数据N<=100 输出格式:对每组测试数据输出两个整数,表示小杉挑选出来的一对翅膀。 注意,比较短的在前,如果有多对翅膀的完美程度一样,请输出最小的一对。 陨石的秘密(NOI’2001) 一、问题描述 公元11380年,一颗巨大的陨石坠落在南极。于是,灾难降临了,地球上出现了一系列反常的现象。当人们焦急万分的时候,一支中国科学家组成的南极考察队赶到了出事地点。经过一番侦察,科学家们发现陨石上刻有若干行密文,每一行都包含5个整数: 1 1 1 1 6 0 0 6 3 57 8 0 11 3 2845 著名的科学家SS发现,这些密文实际上是一种复杂运算的结果。为了便于大家理解这种运算,他定义了一种SS表达式: 1. SS表达式是仅由‘{’,‘}’,‘[’,‘]’,‘(’,‘)’组成的字符串。 2. 一个空串是SS表达式。 3. 如果A是SS表达式,且A中不含字符‘{’,‘}’,‘[’,‘]’,则(A)是SS表达式。 4. 如果A是SS表达式,且A中不含字符‘{’,‘}’,则[A]是SS表达式。 5. 如果A是SS表达式,则{A}是SS表达式。 6. 如果A和B都是SS表达式,则AB也是SS表达式。 例如 ()(())[] {()[()]} {{[[(())]]}} 都是SS表达式。 而 ()([])() [() 不是SS表达式。 一个SS表达式E的深度D(E)定义如下: 例如(){()}[]的深度为2。 密文中的复杂运算是这样进行的: 设密文中每行前4个数依次为L1,L2,L3,D,求出所有深度为D,含有L1对{},L2对[],L3对()的SS串的个数,并用这个数对当前的年份11380求余数,这个余数就是密文中每行的第5个数,我们称之为“神秘数”。 密文中某些行的第五个数已经模糊不清,而这些数字正是揭开陨石秘密的钥匙。现在科学家们聘请你来计算这个神秘数。 输入文件(secret.in) 共一行,4个整数L1,L2,L3,D。相邻两个数之间用一个空格分隔。 (0≤L1≤10,0≤L2≤10,0≤L3≤10,0≤D≤30) 输出文件(secret.out) 共一行,包含一个整数,即神秘数。 输入样例 1 1 1 2 输出样例 8 二、分析解答 这是一个典型的计数问题。 动态规划的一个重要应用就是组合计数—如鱼得水,具有编程简单、时空复杂度低等优点。我们自然想到:是否本题也可以用动态规划来解决呢? 条件的简化 题目对于什么是SS表达式做了大量的定义,一系列的条件让我们如坠雾中。为了看清SS表达式的本质,有必要对条件进行简化。 条件1描述了SS表达式的元素。 条件3、4、5实际上对于()、[]、{}的嵌套顺序做了限制,即()内不能嵌套[]、{},[]内不能潜逃{}。概括起来是两点:SS表达式中括号要配对;{}、[]、()从外到内依次嵌套。 状态的表示 这是动态规划过程中首先要解决的一个问题。本题的条件看似错综复杂,状态不易提炼出来,实际上,题目本身已经为我们提供了一个很好的状态表示法。 对于一个表达式来说,它含有的元素是“(”,“)”,“[”,“]”,“{”,“}”,此外,定义了深度这一概念。最简单的一种想法是:按照题目的所求,直接把{}的对数l1、[]的对数l2、()的对数l3以及深度d作为状态表示的组成部分,即用(l1,l2,l3,d)这样一个四元组来确定一个状态。令F(l1,l2,l3,d)表示这样一个状态所对应的神秘数,于是F(L1,L2,L3,D)对应问题答案。此外,我们令G(l1,l2,l3,d)表示含有l1个{},l2个[],l3个(),深度不大于d的表达式个数。显然,F(l1,l2,l3,d)=G(l1,l2,l3,d)-G(l1,l2,l3,d-1)。于是求解F的问题,可以转化为求解G的问题。 状态转移方程的建立 设当前的状态为(l1,l2,l3,d),根据表达式的第一位的值,分如下三种情况: 情况一:第一位是“(”,与其配对的“)”位于第i位。设表示这种情况下的总数,、类似定义。 ()将整个表达式分成两部分(图中的ss1和ss2)。根据乘法原理,我们只需对两部分分别计数,然后乘起来即为结果。 我们设ss1中含有x对{},y对[],z对()。因为ss1外层已经由一对()括起来,故其内部不可再含[]、{},因此x=0,y=0,且ss1的深度不可超过d-1,ss1的数目为G(x,y,z,d-1)=G(0,0,z,d-1)。ss2中含有l1-x=l1个{},l2-y=l2个[],l3-z-1个(),深度不可超过d,ss2的数目为G(l1,l2,l3-z-1,d)。据此,我们写出下面这个式子: 情况一计算的复杂度为O(n^5)。 情况二:第一位是“[”,与其配对的“]”位于第i位。 ============================ dp[l1][l2][l3][dd]表示深度小于等于dd的方案数,那么答案是dp[l1][l2][l3][dd]-dp[l1][l2][l3][dd-1] 可以用分块和整块的思想来看这个问题 好像[[()][]] 这类的我们可以说它是整块,[][](),这类的我们可以说它是分块,我们在构建的dp数组的时候就是把其当做是分块来处理,然后使用乘法原理 例如dp[l1][l2][l3][dd],我们可以先构建一个小分块,用小分块的方案数*其实括号能组成的方案数,而这个小分块,其实本身是一个整块 我们来看这个小分块,最外层可以是(),[],{} 如果是(),那么里面必定全部是(),由题意的优先级可知,所以假设用i个()组成小分块,则dp[l1][l2][l3][dd]=dp[0][0][i-1][dd-1]*dp[l1][l2][l3-i][dd] 也就是用i个()组成小分块,已经用掉一个做外层,所以只剩下i-1个,并且深度也应该下降为dd-1,而剩下l1个{},l2个[],l3-i个(),他们再组合,两者相乘 同样的,如果小分块使用[]作为外层,那么里面可以使用[]和(),整个小分块假设使用了j个[],i个(),则dp[l1][l2][l3][dd]=dp[0][j-1][i][dd-1]*dp[l1][l2-j][l3-i][dd] 意思就是,用j个[],i个()去构建小分块,已经用掉一个[]作为外层,因此深度也应该下降为dd-1,剩下l1个{},l2-j个[],l3-i个(),他们再组合,两者相乘 同样的,如果小分块使用{}作为外层,那么里面可以使用{},[],(),假设分别用了k,j,i个,那么dp[l1][l2][l3][dd]=dp[k-1][j][i][dd-1]*dp[l1-k][l2-j][l3-i][dd] 小分块用掉一个{}作为外层,深度也应该下降为dd-1,再用剩下的括号去组合,两者相乘 整个算法中需要按照优先级去枚举小分块最外层的类型,应该()在最外层,接着是[],{},这个也是 值得思考的地方 接着就是记忆化实现,感觉这东西递推不好写 搜索的话就要知道边界 1.l1=0 && l2=0 && l3=0 , dp值为1 1.dd=0时,dp值为0 合唱队形(noi2004) 一、问题描述:N位同学站成一排,音乐老师要请其中的(N-K)位同学出列,使得剩下的K位同学排成合唱队形。 合唱队形是指这样的一种队形:设K位同学从左到右依次编号为1,2…,K,他们的身高分别为T1,T2,…,TK,则他们的身高满足T1<... 你的任务是,已知所有N位同学的身高,计算最少需要几位同学出列,可以使得剩下的同学排成合唱队形。 输入格式:第一行是一个整数N(2<=N<=100),表示同学的总数。第一行有n个整数,用空格分隔,第i个整数Ti(130<=Ti<=230)是第i位同学的身高(厘米)。输出格式 OutputFormat 输出文件:这一行只包含一个整数,就是最少需要几位同学出列 二、分析:分别把每个点看成中间最高的人,两边的人数就是求一下从左端到该点的最长上升子序列、从右端到该点的最长下降子序列加起来。然后判断那个点做中间点时需要去除的人数最少就行了。 今明的预算方案(noip2006) 一、问题描述金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间金明自己专用的很宽敞的房间。更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置,你说了算,只要不超过N元钱就行”。今天一早,金明就开始做预算了,他把想买的物品分为两类:主件与附件,附件是从属于某个主件的,下表就是一些主件与附件的例子: 主件 附件 电脑 打印机,扫描仪 书柜 图书 书桌 台灯,文具 工作椅 无 如果要买归类为附件的物品,必须先买该附件所属的主件。每个主件可以有0个、1个或2个附件。附件不再有从属于自己的附件。金明想买的东西很多,肯定会超过妈妈限定的N元。于是,他把每件物品规定了一个重要度,分为5等:用整数1~5表示,第5等最重要。他还从因特网上查到了每件物品的价格(都是10元的整数倍)。他希望在不超过N元(可以等于N元)的前提下,使每件物品的价格与重要度的乘积的总和最大。 设第j件物品的价格为v[j],重要度为w[j],共选中了k件物品,编号依次为j1,j2,……,jk,则所求的总和为:v[j1]*w[j1]+v[j2]*w[j2]+ …+v[jk]*w[jk]。(其中*为乘号)请你帮助金明设计一个满足要求的购物单。 输入格式:输入文件的第1行,为两个正整数,用一个空格隔开: N m 其中N(<32000)表示总钱数,m(<60)为希望购买物品的个数。) 从第2行到第m+1行,第j行给出了编号为j-1的物品的基本数据,每行有3个非负整数 v p q(其中v表示该物品的价格(v<10000),p表示该物品的重要度(1~5),q表示该物品是主件还是附件。如果q=0,表示该物品为主件,如果q>0,表示该物品为附件,q是所属主件的编号) 输出格式:输出文件只有一个正整数,为不超过总钱数的物品的价格与重要度乘积的总和的最大值(<200000)。 样例输入 1000 5 800 2 0 400 5 1 300 5 1 400 3 0 500 2 0 样例输出 2200 二、分析:对于每个部件,如果它是主件,那么有5种决策:只要主件,要主件和附件1,要主件和附件2,全要,连主件都不要。剩下的事情就好办了。 草率的审题,可能会得到这样的算法:dp,对每一个物品做两种决策,取与不取。如果取,满足两个条件:1.要么它是主件,要么它所属的主件已经在包里了。2.放进去后的重要度与价格的成绩的总和要比没放进时的大。这两个条件缺一不可的。于是呼,得到如下的动规方程: f[i,j]:=f[i-1,j]; if (i为主件or i的附件在包中)and (f[i,j] then f[i,j]:=f[i,j-v]+v*w; 我们来分析一下复杂度,空间:dp的阶段为n^2,对与每一个阶段都要记录该状态下在包中的物品有哪些(因为要确定附件的主件是否在包中),每个阶段的记录都要O(n)的空间,所以总的就是O(n^3)。时间,一个dp,n^2的外层循环,内部用布尔量加个主附件的对应数组,为O(1),和起来就为O(n^2)的复杂度。可以看的出,时间的需求为32000*60,不成问题。空间32000*60*60,大约要7.5M的空间,在64M的要求下是完全可以的过的。如果用上题目中的一个很隐秘的条件:“每件物品都是10元的整数倍”,就可以把速度在提高十倍。 细细的看题目,还一个很重要的条件我们还没用:“每个主件可以有0个,1个或2个附件”。这貌似不起眼的一句话,却给我们降低复杂度提供了条件。想一想,为什么题目要对附件的个数做限制呢,明显是在降低难度。 对于一套物品(包含主件,所以的附件),我们称为一个属类,对一个属类的物品的购买方法,有以下5种: 1.一个都不买 2.主件 3.主件+附件1 4.主件+附件2 5.主件+附件1+附件2 这五种购买方法也是唯一的五种方法,也就是说对一属类的物品,我们只有上述的5种购买方法。 于是我们很自然的就会想到把物品按物品的属类捆在一起考虑。这样我们把物品的属类作为dp的状态。可以得到如下的dp方程: f[i,j]=max{f[i-1,j]; f[i-1,j-v[i,0]]+v[i,0]*w[i,0]; f[i-1,j-v[i,0]-v[i,1]]+v[i,0]*w[i,0]+v[i,1]*w[i,1]; f[i-1,j-v[i,0]-v[i,2]]+v[i,0]*w[i,0]+v[i,2]*w[i,2]; f[i-1,j-v[i,0]-v[i,1]-v[i,2]]+v[i,0]*w[i,0]+v[i,1]*w[i,1]+v[i,2]*w[i,2];} 很显然时间复杂度为O(n^2),空间复杂度为O(n^2),加上利用“每件物品都是10元的整数倍”除以10的优化,本题就很完美的解决了。 初始化也十分关键。 ------------------------------------------------------------------ 实际上 启发式搜索+分支定界也能0.01s AC 方法就是按照重要度排序,然后检查主件附件即可 这是一个典型的树形依赖背包问题,对于这类问题有更强的O ( n *V ) 解法。 用f[x, C]表示给以x为根的子树分配v体积所能得到的最大价值。那么计算过程如下: 枚举x的每个儿子,设当前枚举的儿子为i,物品i的体积为v[i],价值为w[i]; 置f[i] = f[x],之后递归求解f[i, C - v[i]]; 最后更新f[x]数组,即f[x, j] = max ( f[x, j], f[i, j - v[i]] + w[i] ) j = v[i]~C 枚举x的儿子如果朴素地枚举所有n个节点话会造成时间上的浪费;由于只有两个附件,考虑采用邻接表的方式储存子结点,使得总时间复杂度提速到完美的O ( n *V ) 。还有就是本题的10的倍数的优化可以进一步提速,上面已经写有了我就不再废话。我用这个算法的提交结果是0ms。 花店橱窗布置(IOI’99) 一、 问题描述 假设你想以最美观的方式布置花店的橱窗。你有F束花,每束花的品种都不一样,同时,你至少有同样数量的花瓶,被按顺序摆成一行。花瓶的位置是固定的,并从左至右,从1至V顺序编号,V是花瓶的数目,编号为1的花瓶在最左边,编号为V的花瓶在最右边。花束则可以移动,并且每束花用1至F的整数唯一标识。标识花束的整数决定了花束在花瓶中排列的顺序,即如果I<j,则花束I必须放在花束j左边的花瓶中。 例如,假设杜鹃花的标识数为1,秋海棠的标识数为2,康乃馨的标识数为3,所有的花束在放入花瓶时必须保持其标识数的顺序,即:杜鹃花必须放在秋海棠左边的花瓶中,秋海棠必须入在康乃馨左边的花瓶中,如果花瓶的数目大于花束的数目,则多余的花瓶必须空置,每个花瓶中只能放一束花。 每一个花瓶的形状和颜色也不相同。因此,当各个花瓶中放入不同的花束时,会产生不同的美学效果,并以美学值(一个整数)来表示,空置花瓶的美学值为零。在上述例子中,花瓶与花束的不同搭配所具有的美学值,可以用下面式样的表格来表示。 花 瓶 1 2 3 4 5 花 束 1、杜鹃花 7 23 -5 -24 16 2、秋海棠 5 21 -4 10 23 3、康乃馨 -21 5 -4 -20 20 例如,根据上表,杜鹃花放在花瓶2中,会显得非常好看;但若放在花瓶4中则显得很难看。 为取得最佳美学效果,你必须在保持花束顺序的前提下,使花束的摆放取得最大的美学值。如果具有最大美学值的摆放方式不止一种,则其中任何一种摆放方式都可以接受,但你只右输出其中一种摆放方式。 假设条件(Asumption) 1≤F≤100,其中F为花束的数量,花束编号从1至F。 F≤V≤100,其中V是花瓶的数量。 -50≤Aij≤50,其中Aij 是花束i在花瓶j中时的美学值。 输入(Input) 输入文件是正文文件(text file),文件名是flower.inp。 第一行包含两个数:F、V。 随后的F行中,每行包含V个整数,Aij即为输入文件中第(i+1)行中的第j个数。 (4)输出(Input) 输出文件必须是名为flower.out的正文文件,文件应包含两行: 第一行是程序所产生摆放方式的美学值。 第二行必须用F个数表示摆放方式,即该行的第K个数表示花束K所在的花瓶的编号。 (5)例子 flower.inp: 3 5 7 23 —5 —24 16 5 21 —4 10 23 —21 5 —4 —20 20 flower.out: 53 4 5 (6)评分 程序必须在2秒钟内运动完毕。 在每个测试点中,完全正确者才能得分。 二、分析 《花店橱窗布置问题》讲的是:在给定花束顺序的前提下,如何将花束插入到花瓶中,才能产生最大美学值。 下面我们分析一下该题的数学模型。 三、数学模型的建立 考虑通过有向图G来建立数学模型。假设有F束花,V个花瓶,我们将第i束花插入第j号花瓶看成一个点(i,j),点(i,j)具有一个权值,就是第i束花插在第j号花瓶中所产生的美学值A(i,j)。 为了体现出花束摆放的顺序,从(i,j)向点(i+1,k)做有向弧,其中k>j。 增加源点S=(0,0)和汇点T=(F+1,V+1)。点S向点(1,k) 做有向弧,点(F,k) 向点T做有向弧,其中1≤k≤V。S和T的权均为0。 设f为图G中S到T的有向路径集合,g为满足题设的花束摆放集合。下面,我们建立fàg的一一映射: 由图G的构造可知,对于任何一条从S到T且长度为k的有向路径P=(i0,j0)à(i1,j1)à…(ik,jk),有ix=ix-1+1,jx>jx-1(1≤x≤k)。而(i0,j0)=S=(0,0),所以i0=0。又ix=ix-1+1,(ik,jk)=T=(F+1,V+1),所以ix=x,k=F+1。我们把第x(1≤x≤F)束花放在第jx号花瓶中,由于jx>jx-1,该方案显然符合题目的条件。对于任意的一个满足题设的摆放方案,我们都可以类似的从图G中找到一条从S到T的有向路径P与之对应。另外,路径P上各顶点的权值之和为∑(x=1..F)A(x,jx),正是该路径对应方案所产生的美学值。 注意到图G中没有环,这一点可以用反证法证明:若图G中有一条有向圈P=(i0,j0)à(i1,j1)à…à(ik,jk),其中(i0,j0)=(ik,jk),而i0 根据上面的分析,如果我们将顶点上的权值看做是引向该顶点的弧的长度,则该问题的实质是求一个有向无环图的最长路径。 四、动态规划求解模型 求有向无环图的最长路径,一个比较好的算法是动态规划。我们按照花束来分阶段。设P[i,j]表示从原点S到顶点(i,j)的最长路径的长度。由图G的构造可知,只有(i-1,0),(i-1,1),…,(i-1,j-1)到(i,j)有有向弧,且弧长都是A(i,j)。也就是说,从S到(i,j)的最长路径长度,必然是由S到(i,k)的最长路径长度加上A(i,j)所得,其中0≤k≤j-1。因此,我们有动态规划方程: P[0,0]=0 P[i,0]=-∞(1≤i≤F+1) P[i,j]=Max(0≤k≤j-1){P[i-1,k]}+A(i,j)(1≤i≤F+1,1≤j≤V+1) ① 最大美学值即为P[F+1,V+1]。 该算法的时间复杂度为O(FV2),仍然存在优化的余地。 设Q[i,j]=Max(0≤k≤j){P[i,k]},代入①式,得 P[i,j]=Q[i-1,j-1]+A(i,j) ② 而Q[i,j]=Max{Q[i,j-1],P[i,j]} ③ 将②代入③,得 Q[i,j]=Max{Q[i,j-1],Q[i-1,j-1]+A(i,j)} 这样,我们有改进后的动态规划方程: Q[0,0]:=0 Q[i,0]:=-∞(1≤i≤F+1) Q[i,j]:=Max{ Q[i,j-1],Q[i-1,j-1]+A(i,j)}(1≤i≤F,1≤j≤V) 最大美学值即为Q[F,V]。 改进后的算法时间复杂度和空间复杂度都是O(FV)。由于1≤F,V≤100,这样的复杂度是可以接受的。 五、小结 上述动态规划方程是在有向图无环G的基础上得到的。如果设Qij表示前i束花放在前j号花瓶中所得到的最大美学值,同样可以得到上面的规划方程,而且同样容易理解。 化工厂装箱员 一、问题描述:118号工厂是世界唯一秘密提炼锎的化工厂,由于提炼锎的难度非常高,技术不是十分完善,所以工厂生产的锎成品可能会有3种不同的纯度,A:100%,B:1%,C:0.01%,为了出售方便,必须把不同纯度的成品分开装箱,装箱员grant第1次顺序从流水线上取10个成品(如果一共不足10个,则全部取出),以后每一次把手中某种纯度的成品放进相应的箱子,然后再从流水线上顺序取一些成品,使手中保持10个成品(如果把剩下的全部取出不足10个,则全部取出),如果所有的成品都装进了箱子,那么grant的任务就完成了。 由于装箱是件非常累的事情,grant希望他能够以最少的装箱次数来完成他的任务,现在他请你编个程序帮助他。 输入格式:第1行为n(1<=n<=100),为成品的数量,以后n行,每行为一个大写字母A,B或C,表示成品的纯度。 输出格式:仅一行,为grant需要的最少的装箱次数。 二、分析dp 应该是这样的:f[ii,i,j,k] 表示 已经把ii个产品放入箱中 现在 手中的 三种物品 分别有 i,j,k个 的最优次数 有三种转移: 装a:f[ii+i,x,j+y,k+z]:=min(f[ii,i,j,k]+1,f[ii+i,x,j+y,k+z]); 装b:f[ii+j,i+x,y,k+z]:=min(f[ii,i,j,k]+1,f[ii+j,i+x,y,k+z]); 装c:f[ii+k,i+x,j+y,z]:=min(f[ii,i,j,k]+1,f[ii+k,i+x,j+y,z]); 分别对应把 这次操作 装的是 a, b,c, 物品; x,y,z 是装入物品后又从后面拿了一些物品以补齐10个对应的 a,b,c, 产品个数 那么外层枚举ii,i,j,k里面再枚举l来统计x,y,z; 初始化f清最大值f[0,x,y,z]:=0; (x,y,x为 前十个 中 a,b,c 件数) 这样就 搞定了 DP不用说,因为物品只有三种,而且手中最多有10个物品,所以考虑手中物品各多少时所装箱的最少的次数,所以设立状态f[i,j,k,l]表示前i个物品,手中A有j个,手中B有k个,手中C有l个的最小装箱次数,那么决策就考虑在这个状态时,可以推到哪些状态,比如说把A全部装进去,那么f[i,j,k,l]+1=f[i+j,0,k,l],因为把A都装进去了,所以A就是0了,同样B和C也是这么推的,最后在f[n,i,j,k]找个最小就可以了。 欢乐的聚会spfa+dp 一、问题描述:聚会上一共有n个地区,编号从1到n,(1<=n<=1000)。经过飘飘乎居士的计算共有p(0 输入格式:第一行,三个整数n p k 接下来p行,每行3个整数ai bi li(数据保证ai与bi之间只有一条道路相连),表示编号为ai与bi的地区之间有一条道路(道路是双向的),并且如果飘飘乎居士选择通过这条道路,那么他将消耗li的体力值。 输出格式:一行,表示飘飘乎居士消耗的最小体力值是多少?如果不能到达,则输出-1 二、分析:先回顾下bell man算法的核心思想 方程 d[v]=min{d[v],d[u]+map[u][v]}采用迭代的思想,对这个方程计算 而这题,可以得到一个类似的方程: 用f[v][k]表式到达v节点使用k次飘飘神功耗费的最小体力值。 那么方程应该是f[v][k]=min{f[v][k],f[u][k-1],max{f[u][k], map[u][k]}}。其中u和v要有路相连。 这个方程看似无法入手,但是一旦我们应用bellman的思想,对方程进行迭代,那么最后便可以得到最优解。 x是当前节点,y是与x相邻的节点.w[x,y]表示x到y的路径长度,k是到达y时用了多少次飘逸...那么f[y,k]:=min{f[x,k-1],max{f[x,k],w[x,y]}}就这样一直松弛下去就ok了 小胖守皇宫(tree dp) 一、问题描述:huyichen世子事件后,xuzhenyi成了皇上特聘的御前一品侍卫。皇宫以午门为起点,直到后宫嫔妃们的寝宫,呈一棵树的形状;某些宫殿间可以互相望见。大内保卫森严,三步一岗,五步一哨,每个宫殿都要有人全天候看守,在不同的宫殿安排看守所需的费用不同。可是xuzhenyi手上的经费不足,无论如何也没法在每个宫殿都安置留守侍卫。帮助xuzhenyi布置侍卫,在看守全部宫殿的前提下,使得花费的经费最少。 输入格式:输入文件中数据表示一棵树,描述如下:第1行 n,表示树中结点的数目。 第2行至第n+1行,每行描述每个宫殿结点信息,依次为:该宫殿结点标号i(0 对于一个n(0 < n <= 1500)个结点的树,结点标号在1到n之间,且标号不重复。 输出格式:输出文件仅包含一个数,为所求的最少的经费。 二、分析 可以看出对于每一个宫殿都有三种状态, 1:该宫殿没有人守卫也没有被子节点控制 2:该宫殿没有人守卫,但是被子节点控制 3:该宫殿有人守卫 Son[I,j]表示i的第j个儿子,fee[i]表示在i点守卫的费用 对于f[I,1],f[I,2],f[I,3]分别表示上述三种状态,那么我们可以得到状态转移方程 F[I,1]=sum(f[son[I,j],2]) F[I,2]=sum(min(f[son[I,j],2],f[son[I,j],3]))+t F[I,3]=sum(min(f[son[I,j],1],f[son[I,j],2],f[som[I,j],3]))+fee[i] 其中t的值要另外考虑如果t=min(f[sun[I,j],3]-f[son[I,j],2]) 如果t>0那么第二种状态要加上t,因为在i的子节点中必须有一个是出于第三种状态 都是树形的数据结构,满足无后效性,适用于DP。采用记忆化搜索的办法,效率比较高,具体的可以参考国家队徐持衡的论文《浅谈几类背包题》。对于每个根节点,有三种看守的办法。分别是在根节点,在子节点,在父节点上,用f[i,1],f[i,2],f[i,3],记录最小代价。 f[k,1]:=min(min(f[i,1],f[i,2]),f[i,3])+f[k,1];把每个子节点所需要的最小代价加起来,再加上守护k位置所需的代价。 f[k,2]:=min(f[i,1],f[i,2])+f[k,2];把每个子节点所需的最小代价加起来,然后还要求其中一个字节点有人看守。 f[k,3]:=min(f[i,1],f[i,2])+f[k,3];这是为了对应一种情况:有人看守->没人->没人->有人,箭头所指的都是子节点,这样在根节点选择时就可以考虑到所有的情况了 活动安排(xtu2012) 一、问题描述:作为一名即将毕业大学生,小明即将参加一系列的面试,每场面试都有一个开始时间Si和一个结束时间Ti。小明可以选择参加面试或者放弃面试,但是迟到和早退是不允许的。每场面试对小明心都有不同的价值Vi。请你帮小明安排一些互不冲突的面试,使得最后参加面试的总价值最大。 输入:有多组测试数据。每组数据的第一行是一个整数1 ≤ N ≤ 100000。接下来N行,每行有三个整数0 ≤ Si< Ti ≤ 1000000000, -100000 ≤Vi ≤ 100000. 输出:对每组测试数据,输出最大的总价值。 二、分析:由于数据比较大,可以先离散化,按结束时间排序,然后按时间背包 有向树k中值问题 一、问题描述:给定一棵有向树T,树T 中每个顶点u都有一个权w(u);树的每条边(u,v)也都有一个非负边长d(u,v)。有向树T的每个顶点u 可以看作客户,其服务需求量为w(u)。每条边(u,v)的边长d(u,v)可以看作运输费用。如果在顶点u 处未设置服务机构,则将顶点u 处的服务需求沿有向树的边(u,v)转移到顶点v 处服务机构需付出的服务转移费用为w(u)*d(u,v)。树根处已设置了服务机构,现在要在树T中增设k处服务机构,使得整棵树T 的服务转移费用最小。对于给定的有向树T,编程计算在树T中增设k处服务机构的最小服务转移费用。 二、分析:一开始想的是二维的状态f[t,k]表示节点t分到了k个设置服务机构任务,但是发现有一个服务转移费用,它会根据距离的变化而变化,而假如说同样是t号节点分到了k个服务机构,那么如果t号节点不设置服务机构,那么他的服务转移费用要找到v(v号点指与t号点间接或直接相连并且设置了服务机构)号点,但是v号点也是不确定位置的,状态表示不完全,所以要加设一维表示离t号点最近的v号点,那么这样f[t,p,k]:=min(Σdfs(son[t],p,k)+dis[t,p]*tree[t].data{t号节点不设置服务机构},Σdfs(son[t],t,k-1) {在t号点设置服务机构}) . 服务转移费用可以先用Floyd预处理好. http://blog.sina.com.cn/s/blog_8442ec3b0100vmpd.html http://blog.csdn.net/five213ddking/article/details/6727927 CEOI1998 Substract 一、问题描述:题目大意:给出一列数,可以对这列数进行一种操作con([a1,a2...an],c)表示把a1,a2...an这列数中的ac,a(c+1)取出,再把ac-a(c+1)放回原处,显然,每操作一次序列长度减1.求一个长度为n-1的操作顺序,使得第一个操作以初始序列为操作对象,从第二个操作开始每个操作都以上一个操作得到的序列为操作对象,并使得最后剩下的数为t.可以假定对于输入至少有一个可行的操作序列. 二、分析:DP求解.我们发现,我们完全可以先不考虑操作的问题.对一个操作而言,它相当于在两个数之间加入了一个减号,而操作顺序其实就代表着括号.如果我们把形成的这个只由减号和括号组成的表达式展开,我们发现,这就是一个只有加减运算的表达式.这时DP就有思路了. 我们记原序列为a,在第i个数后面的运算符称为第i个运算符.f[i,j,k]表示前i个运算符,最后一个运算符为j,true表示是加号,false表示是减号,前i+1个数的运算结果为k是否可能,则可以得出状态转移方程: d[i][j]表示前i个数获得j结果是否可能 状态转移为 d[i][j]=d[i-1][j-a[i-1]||d[i-1][j+a[i-1] 最后把加减序列提取出来转化成最后结果 while 序列长度大于二 do if 序列第三个是+ then 输出2,删除序列第三个 else 输出1,删除序列第二个 end if end while 输出1 古城之谜(Noi2000) 一、问题描述:著名的考古学家石教授在云梦高原上发现了一处古代城市遗址。让教授欣喜的是在这个他称为冰峰城(Ice-Peak City)的城市中有12块巨大石碑,上面刻着用某种文字书写的资料,他称这种文字为冰峰文。然而当教授试图再次找到冰峰城时,却屡屡无功而返。 幸好当时教授把石碑上的文字都拍摄了下来,为了解开冰峰城的秘密,教授和他的助手牛博士开始研究冰峰文,发现冰峰文只有陈述句这一种句型和名词(n)、动词(v)、辅词(a)这三类单词,且其文法很简单: <文章> ::= <句子> { <句子> } <句子> ::= <陈述句> <陈述句> ::= <名词短语> { <动词短语> <名词短语> } [ <动词短语> ] <名词短语> ::= <名词> | [ <辅词> ] <名词短语> <动词短语> ::= <动词> | [ <辅词> ] <动词短语> <单词> ::= <名词> | <动词> | <辅词> 注:其中<名词>、<动词>和<辅词>由词典给出,“::=”表示定义为,“|”表示或,{}内的项可以重复任意多次或不出现,[]内的项可以出现一次或不出现。 在研究了大量资料后,他们总结了一部冰峰文词典,由于冰峰文恰好有26个字母,为了研究方便,用字母a到z表示它们。 冰峰文在句子和句子之间以及单词和单词之间没有任何分隔符,因此划分单词和句子令石教授和牛博士感到非常麻烦,于是他们想到了使用计算机来帮助解决这个问题。假设你接受了这份工作,你的第一个任务是写一个程序,将一篇冰峰文文章划分为最少的句子,在这个前提下,将文章划分为最少的单词。 二、分析:状态设定 F[i,j,k]表示,前i个字母,末尾单词词性为j,组成第k个句子的最少单词数。文章长度为M。 状态转移方程:满足文章中第[a+1,i]可以匹配一个单词,则可以状态转移。i-L<=a<=i-1 且 a>=0,L为所有单词最大长度。 如果匹配的单词为名词 F[i,0,k]=Min {F[a,j,k] + 1 | j=1或j=3, F[a,j,k-1] + 1 | j=0或j=1 } 如果匹配的单词为动词 F[i,1,k]=Min {F[a,j,k] + 1 | j=0或j=2 } 如果匹配的单词为辅词 F[i,2,k]=Min {F[a,j,k] + 1 | j=0或j=2 } F[i,3,k]=Min {F[a,j,k] + 1 | j=1或j=3, F[a,j,k-1] + 1 | j=0或j=1 } 边界条件:F[0,0,0]=0 目标结果:找到最小的k,使得Min{F[M,0,k],F[M,1,k]}有意义,则最小的句子数为k,单词数为Min{F[M,0,k],F[M,1,k]}。 时间复杂度为O(NML),匹配单词的时候可以用Trie树,第三维状态可以使用滚动数组。 http://www.byvoid.com/blog/noi-2000-solution http://starforever.blog.hexun.com/3002063_d.html 单词的划分(tyvj1102) 一、问题描述:有一个很长的由小写字母组成字符串。为了便于对这个字符串进行分析,需要将它划分成若干个部分,每个部分称为一个单词。出于减少分析量的目的,我们希望划分出的单词数越少越好。你就是来完成这一划分工作的。 输入格式:第一行,一个字符串。(字符串的长度不超过100)第二行一个整数n,表示单词的个数。(n<=100)第3~n+2行,每行列出一个单词。 输出格式:一个整数,表示字符串可以被划分成的最少的单词数。 二、分析:用f[i]表示到i为止所用的最少的单词数,则有: f[i]:=Min(f[k])+1;{如果k到i是一个合法的单词,1<=k 边界f[0]:=0;其它的位置填一个大数。 目标f[length(s)]; 核心代码: 其中s是原始串,long[i]表示第i个单词的长度,word[i]表示第i个单词。 for i:=1 to l do for j:=n downto 1 do if i>=long[j] then ifcopy(s,i-long[j]+1,long[j])=word[j] then if f[i-long[j]]+1 f[i]:=f[i-long[j]]+1; 注意就是,区别与背包,背包一般的话外层循环物品,内层循环体积。因为这样比较快。(循环用的定初值次数比较少。)但是这道题不能这么做,自己可以试下。注意第4个猥琐点。 统计单词个数(Noip2001) 一、问题描述:给出一个长度不超过200的由小写英文字母组成的字母串(约定;该字串以每行20个字母的方式输入,且保证每行一定为20个)。要求将此字母串分成k份(1 单词在给出的一个不超过6个单词的字典中。要求输出最大的个数。 输入格式:第一行有二个正整数(p,k),p表示字串的行数;k表示分为k个部分。 接下来的p行,每行均有20个字符。再接下来有一个正整数s,表示字典中单词个数。(1<=s<=6) 接下来的s行,每行均有一个单词。 输出格式:输出一个整数,即最大的个数 二、分析: dp方程好推:f[i,j]:=max(f[k,j-1]+num[k+1,i]); 条件限制:ifk>j-1 num[i,j]表示i到j单词的多少,关键是推num数组。 在这里,若找到一个最短的单词则将相应的num数组加1,是一个很巧的办法。 wlen数组表示以i为首字母,能形成单词的最小长度,不能形成的话wlen[i]=maxn,g数组表述从i开始j个字所形成的字符串中所能形成的单词个数,对于p<=q<=p+i-1,若wlen[q]存在(<>maxn)且q+wlen[q]-1<=p+i-1,则g[i,j]:=g[i,j]+1. 状态转移方程:f[i,u]:=max(f[i-j,u-1]+g[i-j+1,j])(1<=j<=i-1),注意,当i-j 括号序列—tyvj1193 定义如下规则序列(字符串): 1.空序列是规则序列; 2.如果S是规则序列,那么(S)和[S]也是规则序列; 3.如果A和B都是规则序列,那么AB也是规则序列。 例如,下面的字符串都是规则序列: (),[],(()),([]),()[],()[()] 而以下几个则不是: (,[,],)(,()),([() 现在,给你一些由‘(’,‘)’,‘[’,‘]’构成的序列,你要做的,是找出一个最短规则序列,使得给你的那个序列是你给出的规则序列的子列。(对于序列a1,a2,…,和序列bl,b2,…, ,如果存在一组下标1≤i1 输入格式:输入文件仅一行,全部由‘(’,‘)’,‘]’,‘]’组成,没有其他字符,长度不超过255。 输出格式:添加括号最少的数目 样例输入:[[(([] 样例输出:4 二、分析:())()( -> (把可以匹配的括号去掉) )()( -> )( .最后就只剩下两个了,这两个就用添加括号来满足吧。。。那么,不就是把两种括号分开来搞?但是这种贪心肯定是错的。举个很显然的例子:[(]) 如果贪心判断,那么上面那个例子就是合法的。。。显然,上面那个例子不合法。。。然后dp f[i][j]:把i..j修改为合法序列所需要添加的最少的括号是多少个 注意:但是最后还要加上一步。枚举k= i .. j f[i][j] = min(f[i][j], f[i][k] + f[k+1][j] ) 括号序列poj1141 题意就是上面一题,但是输出是输出改后的序列 分析: 一个序列如果 是AB形式的话,我们可以划分为A,B两个子问题;而如果序列是[A]或者(A)的形式,我们可以把它降为分析A即可。分解的底层就是剩下一对[]或者 ()或者是只剩下一个单字符就停下不再分解。当剩下的是一对匹配的()或者[]时,我们不必添加如何括号,因为这已经匹配,而对于只剩下最后一个单字符,我们需要对它配一个字符,使它配对,如(就配上),]就配上[,依此类推。 那么这题的状态转移方程就很容易列出来了,用a[i,j]表示从位置i到位置j所需要插入的最小字符数,明显有状态转移方程如下: a[i,j]=min(a[i,k]+a[k+1,j])其中i<=k 特别的,当a[i,j]的首尾为()或者[]时, a[i,j] =min(a[i+1,j-1],tmp) 其中tmp为上面根据性质3求得的最小值,这条转移是利用了性质2。 初始条件为: a[i,i]=1,表示任意一个字符都要一个对应的字符来匹配; a[i+1,i]=0.这个没有什么实际的意义,只是前面的分析说了,当剩下一对()或者[]时,就不再继续往下分解,而我们为了更方便的组织程 序,把当剩下一对()或者[]时还继续分解,那么,举例子来说,本来序列为(),a[0,1]通过转移变成a[1,0],为了不出错,所以我们把a[i+ 1,i]初始化为0,这样组织程序起来也就比较容易了。 到这里,转移方程就结束了,如果这题只让你求最少需要插入的字符数,那么这题就结束了,而这题让你求的是包含子序列的最小regular brackets sequence,所以我们还需要对前面的求解过程进行标记,把每次求得最小值所取的位置都记录下来,然后用递归回溯的方法去求得最小的regular brackets sequence。 如:我们用tag[i,j]表示i到j位置中记录下来该到哪里划分,假设初始化为-1, 如果a[i,j]选择最优的时候,选择的是a[i,k]+a[k+1,j],那么记录下k的位置; 如果a[i,j]选择的是a[i+1,j-1]的话,那么保持初始值即可。 这样再根据a[0,strlen(str)-1]逐步回溯。 棋盘分割(NOI’99,poj1191) 一、问题描述 将一个8×8的棋盘进行如下分割:将原棋盘割下一块矩形棋盘并使剩下部分也是矩形,再将剩下的部分继续如此分割,这样割了(n-1)次后,连同最后剩下的矩形棋盘共有n块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行) 原棋盘上每一格有一个分值,一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成n块矩形棋盘,并使各矩形棋盘总分的均方差最小。 请编程对给出的棋盘及n,求出的最小值。 输入 第1行为一个整数n(1 第2行至第9行每行为8个小于100的非负整数,表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。 输出 仅一个数,为(四舍五入精确到小数点后三位)。 样例输入 3 1 1 1 11 1 1 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 0 3 样例输出 1.633 二、初步分析 本题的实质是求一种最优的棋盘分割方式,使得每块棋盘与平均值的差值之和最小。 首先我们必须明确几个条件(关键字),这样对我们理解题意进而采取正确的算法解决问题大有帮助: 于是我们开始考虑算法:对比八皇后问题的复杂度,我们不难看出这道题需要搜索更多的内容,在时间上搜索算法实不可取;因此,只能使用动态规划实现本题。经过分析,不难发现本题符合最优化原理:即若第i次分割为最佳分割,则第i-1次分割为且必为最佳;定义函数F[i,j][i’,j’]为[i,j]、[i’,j’]分别为左上、右下角的棋盘的最优值,F0[i,j][i’,j’]为[i,j]、[i’,j’]分别为左上、右下角的棋盘值,探寻函数F[i,j][i’,j’]的动态转移方程。 下面分析分割方式。当我们进行第i次分割时不外乎以下四种方式: 逐一进行分析:(图3.4-3) 1. 横割方式: a) 第i次切割将棋盘分为上i-1个棋盘和下1个棋盘(图(a)) A1=F0[i1,j1][i’,j2]+F[i’+1,j1][i2,j2] b) 第i次切割将棋盘分为下i-1个棋盘和上1个棋盘(图(b)) A2=F[i1,j1][i’,j2]+F0[i’+1,j1][i2,j2] 2. 竖割方式: c) 第i次切割将棋盘分为右i-1个棋盘和左1个棋盘(图(c)) A3=F[i1,j1][i2,j’]+F0[i1,j’+1][i2,j2] d) 第i次切割将棋盘分为左i-1个棋盘和右1个棋盘(图(d)) A3=F0 [i1,j1][i2,j’]+F [i1,j’+1][i2,j2] 状态转移方程为 F[i1,j1][i2,j2]=min{A1,A2,A3,A4} (1<=i1,j1<=8,i1<=i2<=8,j1<=j2<=8,2<=k<=n) 其中k代表分割的棋盘数,单调递增,因此第k次分割只与k-1次的结果有关,所以每做完第k次对棋盘的规划F0ßF。由此节省下许多空间。 三、程序实现 下面我们讨论程序实现的具体步骤与代码的优化。 首先在读入过程段我们进行准备工作,累加计算出F0并统计出棋盘每个格子值之和S来计算平均数Average。 sß0; for i:=1 to 8 do for j:=1 to 8 dobegin read(f[i,j][i,j]);sßs+f[i,j][i,j]; {读入棋盘每个格子的值,并统计其和} for i1:=1 to i do {枚举左上方坐标i1,j1} for j1:=1 to j do fori2:=i to 8 do for j2:=j to 8 do {枚举右上方坐标i2,j2} if (i1<>i) or (j1<>j) or(i2<>i) or (j2<>j) the f[i1,j1][i2,j2]ßf[i1,j1][i2,j2]+f[i,j][i,j]; end; 在套用循环算出F0[i1,j1][i2,j2]的值,此处不再赘述。 然后用动态规划求解: for i:=2 to n do begin {分阶段,第i次分割} for i1:=1 to 8 do for j1:=1 to 8 do for i2:=i1 to 8 do for j2:=j1 to 8 do begin {确定坐上、右下角坐标} F[i1,j1][i2,j2]ßmax; for i’:=i1 to i2-1 do begin 计算A1,A2; F[i1,j1][i2,j2]ßmin{A1,A2}; end; for i’:=i1 to i2-1 do begin 计算A3,A4; F[i1,j1][i2,j2]ßmin{F[i1,j1][i2,j2],A3,A4}; end; end; F 0ßF; end; 三、小结 本题是极有代表性的动态规划题型,较之NOI99的其他题目算是比较简单的。此题的思路简单而明了,没有太多限制条件让人梳理不清,空间的自由度很大,唯一的限制便是运行时间。 所谓窥一斑可见全豹,从本题的思考过程中,我们不难总结出应用动态规划算法的一般思路及步骤: l 确定算法,整体估计可行度。一般从两方面着手:时空复杂度和最优化原理。 l 建立模型,考虑可能出现的情况。 l 建立动态转移方程。 l 程序实现及代码优化。 l 把方差公式先变形为 σ2 =(1/n)∑xi2-xa2,xa为平均值。 由于要求标准差最小,只需方差最小,平均值都是一样的,n也是一样的,这样原问题就变为求这n快小棋盘总分的平方和最小 考虑左上角为(x1,y1),右上角为(x2,y2)的棋盘,设该棋盘切割K次后得到的K+1块矩形的总分平方和最小值为d[k,x1,y1,x2,y2]。该棋盘的总分平方和为 s[x1,y1,x2,y2].则它可以沿着横线切,也可以沿着竖线切,然后选一块继续切(这里可以用递归完成) 状态转移方程为d[k,x1,y1,x2,y2]= min{ min{d[k-1,x1,y1,a,y2] + s[a+1,y1,x2,y2] , d[k-1,a+1,y1,x2,y2] + s[x1,y1,a,y2]}, (x1 <= a < x2) min{d[k-1,x1,y1,x2,b] + s[x1,b+1,x2,y2] , d[k-1,x1,b+1,x2,y2] + s[x1,y1,x2,b]} (y1 <= b < y2 } 聪聪和可可(noi2005) 整个森林可以认为是一个无向图,图中有N个美丽的景点,景点从1至N编号。小动物们都只在景点休息、玩耍。在景点之间有一些路连接。当聪聪得到GPS时,可可正在景点M(M≤N)处。以后的每个时间单位,可可都会选择去相邻的景点(可能有多个)中的一个或停留在原景点不动。而去这些地方所发生的概率是相等的。假设有P个景点与景点M相邻,它们分别是景点R、景点S,……景点Q,在时刻T可可处在景点M,则在(T+1)时刻,可可有1/(P+1)的可能在景点R,有1/(P+1)的可能在景点S,……,有1/(P+1)的可能在景点Q,还有1/(P+1)的可能停在景点M。 我们知道,聪聪是很聪明的,所以,当她在景点C时,她会选一个更靠近可可的景点,如果这样的景点有多个,她会选一个标号最小的景点。由于聪聪太想吃掉可可了,如果走完第一步以后仍然没吃到可可,她还可以在本段时间内再向可可走近一步。在每个时间单位,假设聪聪先走,可可后走。在某一时刻,若聪聪和可可位于同一个景点,则可怜的可可就被吃掉了。灰姑娘想知道,平均情况下,聪聪几步就可能吃到可可。而你需要帮助灰姑娘尽快的找到答案。 输入格式:本题有多组测试数据,每组数据的第1行为两个整数N和E,以空格分隔,分别表示森林中的景点数和连接相邻景点的路的条数。第2行包含两个整数C和M,以空格分隔,分别表示初始时聪聪和可可所在的景点的编号。接下来E行,每行两个整数,第i+2行的两个整数Ai和Bi表示景点Ai和景点Bi之间有一条路。所有的路都是无向的,即:如果能从A走到B,就可以从B走到A。输入保证任何两个景点之间不会有多于一条路直接相连,且聪聪和可可之间必有路直接或间接的相连。 输出格式:对于每组输入,输出一个实数,四舍五入保留三位小数,表示平均多少个时间单位后聪聪会把可可吃掉 二、分析:首先聪聪要逐步向可可靠近,所以我们按照题目要求预处理出p[i][j]表示i -> j的最短路上与i相邻且标号最小的点,可以使用n次spfa来实现。 聪聪下一步所在顶点为p[p[i][j]][j],可可下一步可能在相邻的顶点或者不动,用w[j][i]表示 设计状态:f[i][j]表示聪聪在顶点i,可可在顶点j时聪聪抓住可可的平均步数 边界: 1、当i == j时,f[i][i] = 0; 2、当p[i][j] = j 或者 p[p[i][j]][j] = j时,f[i][j] = 1 这样我们就可以使用记忆化搜索解决这道题 因为2个动物的位置一定的时候,平均步数是定值,所以用f[i,j]表示聪聪在i,可可在j的平均步数。于是当前的平均步数为所有可行的下一步的状态的平均步数的平均数+1(从当前走到下一步的那一步),即f[i,j] = Σ(f[i1,j1]) + 1。 而当前状态生成下一状态需要维护一下当可可走到j1时,聪聪的移向,及处理一个p[i,j1]表示从i出发到j1的最近的一个相邻点。如果如floyed来预处理,时间复杂度达到O(n^2),对于极限数据会超时,而题目声明E<=1000,即这个图是稀疏图,所以可以用n次spfa来处理,因为spfa在稀疏图上的平均时间效率为O(E),能够应付所有的数据。 因为不满足拓朴序,所以需要记忆化搜索。 时间复杂度:预处理(n次spfa)为O(nE),记忆花搜索的时间复杂度为O(n^2),所以总时间复杂度为O(n^2)。 血缘关系 一、题目描述:我们正在研究妖怪家族的血缘关系。每个妖怪都有相同数量的基因,但是不同的妖怪的基因可能是不同的。我们希望知道任意给定的两个妖怪之间究竟有多少相同的基因。由于基因数量相当庞大,直接检测是行不通的。但是,我们知道妖怪家族的家谱,所以我们可以根据家谱来估算两个妖怪之间相同基因的数量。 妖怪之间的基因继承关系相当简单:如果妖怪C是妖怪A和B的孩子,则C的任意一个基因只能是继承A或B的基因,继承A或B的概率各占50%。所有基因可认为是相互独立的,每个基因的继承关系不受别的基因影响。 现在,我们来定义两个妖怪X和Y的基因相似程度。例如,有一个家族,这个家族中有两个毫无关系(没有相同基因)的妖怪A和B,及它们的孩子C和D。那么C和D相似程度是多少呢?因为C和D的基因都来自A和B,从概率来说,各占50%。所以,依概率计算C和D平均有50%的相同基因,C和D的基因相似程度为50%。需要注意的是,如果A和B之间存在相同基因的话,C和D的基因相似程度就不再是50%了。 你的任务是写一个程序,对于给定的家谱以及成对出现的妖怪,计算它们之间的基因相似程度。 输入:第一行两个整数n和k。n(2≤n≤300)表示家族中成员数,它们分别用1,2, …, n来表示。k(0≤k≤n-2)表示这个家族中有父母的妖怪数量(其他的妖怪没有父母,它们之间可以认为毫无关系,即没有任何相同基因)。 接下来的k行,每行三个整数a, b, c,表示妖怪a是妖怪b的孩子。 然后是一行一个整数m(1≤m≤n2),表示需要计算基因相似程度的妖怪对数。 接下来的m行,每行两个整数,表示需要计算基因相似程度的两个妖怪。 你可以认为这里给出的家谱总是合法的。具体来说就是,没有任何的妖怪会成为自己的祖先,并且你也不必担心会存在性别错乱问题。 输出:共m行。可k行表示第k对妖怪之间的基因相似程度。你必须按百分比输出,有多少精度就输出多少,但不允许出现多余的0(注意,0.001的情况应输出0.1%,而不是.1%)。具体格式参见样例。 【输入样例】 7 4 4 1 2 5 2 3 6 4 5 7 5 6 4 1 2 2 6 7 5 3 3 【输出样例】 0% 50% 81.25% 100% 分析:f[i,j]:=(f[father[i],j]+f[mother[i],j])/2或者(f[i,father[j]]+f[i,mother[j]])/2 决斗(rqnoj 458) 一、问题描述:Michel最近迷上了买彩票。现在,某赌场就一轮决斗的结果开设了赌局。这个赌局同样被Michel盯上了,他决定购买这个彩票。 当然,身为有教养有文化的人,Michel买彩票并不是胡乱买的。他在买之前进行了详尽的市场调查,并拿到了任意两个选手对决后的胜败情况。可以假定正式比赛的时候决斗后果也是一样的。 同时决斗的规则是这样的: 首先,选手们围成一个圈。每一回合随机抽出一个选手的号码,让他和他右边的选手决斗。开始时,1号右边的是2号,2号右边的试三号,依此类推。特别的,n号右边的是1号。战败的选手则退出战场。例如2号战败,则1号右边的就变成了3号。 现在,他找到了你,希望你能告诉他哪些选手可能赢。 数据范围:1<=n<=500 输入格式:输入数据的第一行为一个整数n,表示有n个选手。接下来n行,每行n个整数,第I+1行第J列表示第I个选手与第J个选手对决后的胜败情况,0表示选手I失败,1表示选手I获胜。 输出格式:输出数据的第一行为一个整数k,表示有多少选手可能赢。接下来k行,每行一个整数,从小到大输出这些选手的编号。 样例输入:2 0 0 1 0 样例输出:1 2 二、分析:这道题目容易产生下面错解: 设f[i,j]表示第i轮j选手是否可能活下来,所以f[i,j]=f[i,j] or f[i-1,k],k表示可能在i轮与j碰面的人的编号。 首先:f[i][j] 表示 i 能够 打败 j,则需要一个中转 k。分两种情况: 一、要求 i 能打败 k-1,k能打败 j-1,则只剩 i , j , k,此时有三种情况 ①i打败k,i再打败j ②k打败j,i再打败k ③j打败k,i再打败j 二、要求 j 能打败 k-1,k能打败 i-1,则只剩下 i , j , k,下同。。 接下来,为了处理环的问题,我分把上两种情况都分了两种情况。i在j左边和i在j右边。 最后胜利的条件是 i 能打败 i-1(当然,如果i-1=0则i应打败n) 这造成一种混乱,如i能打败i-1,可能只是因为i和i-1相邻且i比i-1厉害,而没有经过和其他人的打架。 但是规划结果与实事不符,因为存在一下一种可能:当j 正确的方法是 f[i][j] 表示 i 能与 j 相遇,这样就简单多了。 f[i][j] =OR(f[i][k]&f[k][j]&(m[i][k]|m[j][k])) 状态表示略微改变,则转移就简单多了。另外。把圈转换成链,即加倍。上述的两种方法则轻松地合并了。如:1与3相遇仍是1与3相遇,而3与1相遇则是3与1+n相遇。省去了分别讨论的麻烦,本来就没有分类讨论的必要,因为我们要求的结果是i和i+n相遇,则i肯定会和k相遇且k和i+n相遇,意思就是分的两类对于我们需要的结果,是都要满足的。 输出时,容易证明,一个人 i 能胜出当且仅当 Meet[i, i + N] 为真,于是扫一遍即可。 跳舞家怀特先生(tyvj1211) 一、问题描述:怀特先生是一个大胖子。他很喜欢玩跳舞机(Dance Dance Revolution, DDR),甚至希望有一天人家会脚踏“舞蹈家怀特先生”。可惜现在他的动作根本不能称作是在跳舞,尽管每次他都十分投入的表演。这也难怪,有他这样的体型,玩跳舞机是相当费劲的。因此,他希望写一个程序来安排舞步,让他跳起来轻松一些,至少不要每次都汗流浃背。 DDR的主要内容是用脚来踩踏板。踏板有四个方向的箭头,用1 (Up)、2 (Left)、3(Down)、4 (Right)来代表,中间位置由0来代表。每首歌曲有一个箭头序列,游戏者必须按照或这个序列一次用某一只脚踩相应的踏板。在任何时候,两只脚都不能在同一踏板上,但可以同时待在中心位置0。 每一个时刻,它必须移动而且只能移动他的一只脚去踩相应的箭头,而另一只脚不许移动。跳完一首曲子之后,怀特先生会计算他所消耗的体力。从中心移动到任何一个箭头耗费2单位体力,从任何一个箭头移动到相邻箭头耗费3单位体力,移动到相对的箭头(1和3相对,2和4相对)耗费4单位体力,而留在原地再踩一下只需要1单位。怀特先生应该怎样移动他的双脚(即,对于每个箭头,选一只脚去踩它),才能用最少的体力完成一首给定的舞曲呢? 例如,对于箭头序列Left (2),Left (2), Up (1), Right (4),他应该分别用左、左、右、右脚去踩,总的体力耗费为2+1+2+3=8单位。 输入:第一行N,表示有N个时刻N<=10000.第二到n+1行,每行一个数,表示需要踩得版 输出:一个数,最小消耗体力 二、分析:动态规划要求状态表示满足无后效性,若以第i步作为当前状态,显然不满足无后效性,因为作哪种决策取决于当前双脚的状态,而这是未知的。因此选当前双脚的位置作为当前状态能满足无后效性。那么此题很明显是一个多状态决策问题了。 用dp[i][j][k]表示从当前状态(左脚的位置为i,右脚的位置为j,已跳了k步)到终状态消耗的最小体力。 dp[i][j][k]=min(dp[i][a[k+1]][k+1]+cost(j,a[k+1]),dp[a[k+1]][j][k+1]+cost(i,a[k+1])). 表示我当前从左脚或者从右脚出发的最小花费 积木游戏(NOI’97) 一、问题描述 一种积木游戏,游戏者有N块编号依次为1,2,…,N的长方体积木。第I块积木通过同一顶点三条边的长度分别为ai,bi,ci(i=1,2,…,N),如图1所示: 游戏规则如下: 1 从N块积木中选出若干块,并将他们摞成M(1<= M <= N)根柱子,编号依次为1,2,…,M,要求第k根柱子的任意一块积木的编号都必须大于第K-1根柱子任意一块积木的编号(2<=K<=M)。 2 对于每一根柱子,一定要满足下面三个条件: 除最顶上的一块积木外,任意一块积木的上表面同且仅同另一块积木的下表面接触; 对于任意两块上下表面相接触的积木,若m,n是下面一块积木接触面的两条边(m>=n),x,y是上面一块积木接触面的两条边(x>=y),则一定满足m.>=x和n>=y; 下面的积木的编号要小于上面的积木的编号。 请你编一程序,寻找一种游戏方案,使得所有能摞成的M根柱子的高度之和最大。 输入数据: 文件的第一行是两个正整数N和M(1<= M <= N <=100),分别表示积木总数和要求摞成的柱子数。这两个数之间用一个空格符隔开。接下来的N行是编号从1到N个积木的尺寸,每行有三个1至500之间的整数,分别表示该积木三条边的长度。同一行相邻两个数之间用一个空格符隔开。 输出数据: 文件只有一行,是一个整数,表示所求得的游戏方案中M根柱子的高度之和。 二、分析 由于题目中条件的限制:(1)积木已经编了号;(2)后面的柱子中的积木编号必须比前面的柱子中的积木编号大:(3)对于同一根柱子,上面的积木的编号必须大于下面的积木的编号,因此使得这道题的无后效性很明显,因为对于第I块积木,它的状态只取决于前I-1块积木,与后面的积木无关。 这样我们很自然地想到了动态规划。下面我们来讨论状态转移方程。由于一块积木可以任意翻转,因此它的上表面有三种情况,对应的三个面的长和宽分别为:a和b, a和c, b和c.。设(1) f[I,j,k]表示以第I块积木的第k面为第j根柱子的顶面的最优方案的高度总合; (2)block[I,k] 记录每个积木的三条边信息(block[I,4]:=block[I,1];block[I,5]:=block[I,2])。其中block[I,j+2]表示当把第I块积木的第j面朝上时所对应的高,即所增加的高度;(3)can[I,k,p,kc]表示第I块积木以其第k面朝上,第p块积木以第kc面朝上时,能否将积木I放在积木p的上面。1表示能,0表示不能。对于f[i,j,k], 有两种可能:(1)除去第I块积木,第j根柱子的最上面的积木为编号为p的,若第p块积木以第kc面朝上,必须保证当第I块积木以k面朝上时能够被放在上面,即can[I,k,p,kc]=1;(2)第I块积木是第j根柱子的第一块积木,第j-1根柱子的最上面为第p块积木,则此时第p块积木可以以任意一面朝上。则有: 输入格式:本题有多组测试数据,每组数据的第1行为两个整数N和E,以空格分隔,分别表示森林中的景点数和连接相邻景点的路的条数。第2行包含两个整数C和M,以空格分隔,分别表示初始时聪聪和可可所在的景点的编号。接下来E行,每行两个整数,第i+2行的两个整数Ai和Bi表示景点Ai和景点Bi之间有一条路。所有的路都是无向的,即:如果能从A走到B,就可以从B走到A。输入保证任何两个景点之间不会有多于一条路直接相连,且聪聪和可可之间必有路直接或间接的相连。 输出格式:对于每组输入,输出一个实数,四舍五入保留三位小数,表示平均多少个时间单位后聪聪会把可可吃掉 二、分析:首先聪聪要逐步向可可靠近,所以我们按照题目要求预处理出p[i][j]表示i -> j的最短路上与i相邻且标号最小的点,可以使用n次spfa来实现。 聪聪下一步所在顶点为p[p[i][j]][j],可可下一步可能在相邻的顶点或者不动,用w[j][i]表示 设计状态:f[i][j]表示聪聪在顶点i,可可在顶点j时聪聪抓住可可的平均步数 边界条件: f[1,1,1]:=block[1,1,3]; f[1,1,2]:=block[1,1,4];f[1,1,3]:=block[1,1,5]; f[I,0,k]:=0; (1<= I <= n, 1<= k <= 3); 此算法主要需要存储block,can和f数组,分别需要O(n),O(n^2)和 O(n*m),总和约为120K。时间复杂度为O(n^2*m),约为10^6. 方法二: 1. dp[k][i][j][s] 表示在前 i 个积木分成 k 堆,并且第 k 堆最上面的积木编号为 j,j 的 s 面朝上(s = 0, 1,2); 2. 第 i 个积木有 3 种决策: a.dp[k][i][i][t] = min(dp[k][i-1][j][s]); 放在第 k 堆; b.dp[k][i][i][t] = min(dp[k-1][i-1][j][s]); 另起一堆; c.dp[k][i][j][s] = dp[k][i-1][j][s]; 不参与; 3. 由于摆在上面的边要小于等于摆在下面积木的边,所以事先可以对 a, b, c 边从小到大排序下,判断的时候更加方便; 4. 对于循环中的 t, s 变量,则是控制上、下积木朝向的。我们每次交换边的值,只让 b, c 比较,使代码看起来更加清爽; 逃学的小孩(NOI2003) 一、问题描述:Chris家的电话铃响起了,里面传出了Chris的老师焦急的声音:“喂,是Chris的家长吗?你们的孩子又没来上课,不想参加考试了吗?”一听说要考试,Chris的父母就心急如焚,他们决定在尽量短的时间内找到Chris。他们告诉Chris的老师:“根据以往的经验,Chris现在必然躲在朋友Shermie或Yashiro家里偷玩《拳皇》游戏。现在,我们就从家出发去找Chris,一但找到,我们立刻给您打电话。”说完砰的一声把电话挂了。 Chris居住的城市由N个居住点和若干条连接居住点的双向街道组成,经过街道x需花费Tx分钟。可以保证,任两个居住点间有且仅有一条通路。Chris家在点C,Shermie和Yashiro分别住在点A和点B。Chris的老师和Chris的父母都有城市地图,但Chris的父母知道点A、B、C的具体位置而Chris的老师不知。 为了尽快找到Chris,Chris的父母会遵守以下两条规则: l 如果A距离C比B距离C近,那么Chris的父母先去Shermie家寻找Chris,如果找不到,Chris的父母再去Yashiro家;反之亦然 l Chris的父母总沿着两点间唯一的通路行走。 显然,Chris的老师知道Chris的父母在寻找Chris的过程中会遵守以上两条规则,但由于他并不知道A,B,C的具体位置,所以现在他希望你告诉他,最坏情况下Chris的父母要耗费多长时间才能找到Chris? 例如上图,这座城市由4个居住点和3条街道组成,经过每条街道均需花费1分钟时间。假设Chris住在点C,Shermie住在点A,Yashiro住在点B,因为C到B的距离小于C到A的距离,所以Chiris的父母会先去Yashiro家寻找Chris,一旦找不到,再去Shermie家寻找。这样,最坏情况下Chris的父母需要花费4分钟的时间才能找到Chris。 二、分析:摘自陈瑜希的论文 问题抽象: 本题题意很明确,即在一棵树中,每条边都有一个长度值,现要求在树中选择3个点X、Y、Z,满足X到Y的距离不大于X到Z的距离,且X到Y的距离与Y到Z的距离之和最大,求这个最大值。 粗略分析: 很显然,该题的结构模型是一棵树,而且数据量很大,很容易把这题的方法向在树形结构上使用动态规划上靠拢。考虑任意节点a时,很容易发现,如果以这个点作为题目中要求的节点Y,那么只需要求出离这点最远的两个节点即可。但是在树形结构上,计算出离某个节点最远的两个节点需要的复杂度,而我们并不知道哪个点是答案中的节点Y,所以必须枚举这个点,这样一来,时间复杂度就成了,在N=200000时会严重超时,因此这个方法是不可行的。 枚举Y点的话,会超时,是否就无法加上枚举的思想呢?可以多尝试一些思路。观察这样一棵树: 可以把点3当作点X,点1当作点Y,点6当作点Z,这样就可以得到最大值了。因为|XY|=|YX|,故只需考虑YX和YZ这两条路就可以了。在图中来观察这两条路,可以发现分别是这样走的:YX:1à2à3,YZ:1à2à4à6。来比较这两条路的行程,可以发现,都是从1先到2,然后再分开走各自的路,而且满足从2以后的经过的节点,没有重复的节点。为了方便,我们形象地将点2称为分叉点。如果枚举分叉点,能不能得到一个高效的算法呢?来尝试分析这种想法。 枚举分叉点 将某个点a当作分叉点时,以其为根构造一棵树,对节点Y,就有两种情况:1Y就是节点a;2Y在a的某个孩子节点的子树上。对于情况1,可以把它转化为情况2,只需给a加一个空的孩子节点,认为它和a之间的距离是0即可。既然a是分叉点,那么X和Z就不能在同一棵子树上,X和Y,Y和Z也不能在同一棵子树上。题目中要求的是使|XY|+|YZ|最大,也就是要求2|Ya|+|Za|+|Xa|最大。至此,思路已完全明确,对于以a为分叉点的情形,只需求出到a的最远的3个点,而且这3个点分别处于a的3棵不同的子树之中。如果采用枚举分叉点的方法的话,每次都需要的计算才行,时间复杂度就又成了。 两次遍历 这里,需要改变一下思路。以点1为根,计算出要求的值后,不去枚举其它的节点,而把这棵树再遍历一遍,进行一次BFS,深度小的先访问,深度大的后访问,就保证了访问到某一个节点的时候,其父亲节点已经被访问过了。假设我们现在访问到了点a,我们现在要求的是距点a的3个最远的点,且这3个点到a的路径上不经过除a外的相同节点。显然,这3个点要么位于以a为根的子树中,要么位于以a为根的子树外。如果在以a为根的子树外,那么是一定要通过a的父亲节点与a相连的。至此,思路逐渐清晰起来。此次遍历时,对于点a,检查其父亲节点,只需求出到其父亲节点的最远的,且不在以a为根的子树中的那点即可,再与第一次遍历求得的值进行比较,就可以求出以该点为分叉点时,|XY|+|YZ|的最大值了。具体方法为,每个点记录最大的两个值,并记录这最大的两个值分别是从哪个相邻节点传递来的。当遍历到其某个孩子节点时,只需检查最大值是否是从该孩子节点传递来的,如果是,就取次大值,如果不是,就可以取最大值。这样一来,该算法的时间复杂度和空间复杂度都为,是个非常优秀的算法。 注意 这里提醒大家注意一点,计算过程中的值和最后的结果可能会超过长整型的范围,所以这里需要使用int64或者double类型。 对于树必须进行两次遍历,才能求得最终的最大值。该例题的分析中提出了分叉点的想法,是比较具有创造性的,需要从多个角度思考。因此,在平时的练习中,当对一道题目束手无策时,可从多个角度思考,创造新思维,使题目得到解决。此题遍历两次的方法具有普遍性,在许多题目中都可以得到应用:记录最大的两个值,并记录是从哪个节点传递来的思想方法。这种遍历两次和记录最大的多个值的思想是值得学习的,也是动态规划在树上进行使用的经典方法。
O(n^2)算法分析如下
1、对于a[n]来说,由于它是最后一个数,所以当从a[n]开始查找时,只存在长度为1的不下降子序列;
阶段i:石子的每一次合并过程,先两两合并,再三三合并,...最后N堆合并
状态s:每一阶段中各个不同合并方法的石子合并总得分。
决策:把当前阶段的合并方法细分成前一阶段已计算出的方法,选择其中的最优方案
具体来说我们应该定义一个数组s[i,j]用来表示合并方法,i表示从编号为i的石头开始合并,j表示从i开始数j堆进行合并,s[i,j]为合并的最优得分。
对于上面的例子来说,初始阶段就是s[1,1],s[2,1],s[3,1],s[4,1],s[5,1],s[6,1],因为一开始还没有合并,所以这些值应该全部为0。
第二阶段:两两合并过程如下,其中sum(i,j)表示从i开始数j个数的和
s[1,2]=s[1,1]+s[2,1]+sum(1,2)
s[2,2]=s[2,1]+s[3,1]+sum(2,2)
s[3,2]=s[3,1]+s[4,1]+sum(3,2)
s[4,2]=s[4,1]+s[5,1]+sum(4,2)
s[5,2]=s[5,1]+s[6,1]+sum(5,2)
s[6,2]=s[6,1]+s[1,1]+sum(6,2)
第三阶段:三三合并可以拆成两两合并,拆分方法有两种,前两个为一组或后两个为一组
s[1,3]=s[1,2]+s[3,1]+sum(1,3)或s[1,3]=s[1,1]+s[2,2]+sum(1,3),取其最优
s[2,3]=s[2,2]+s[4,1]+sum(2,3)或s[1,3]=s[2,1]+s[3,2]+sum(2,3),取其最优
...
3.从1到L(压缩后最后一个石子位置)+t-1进行动态规划,f[i]=min{f[i-j]+1(如果i处不为石子),f[i-j](如果i处为石子)}(j=s..t,f[i]初始值为100,最多有100颗石子);
4.答案就是min{f[L],f[L+1],...,f[L+t-1]}。
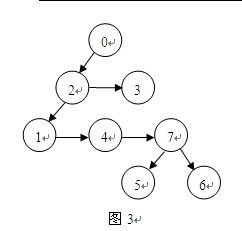
我们添加一个顶点0,并且在每棵树的顶点与0之间连一条边使森林成为一棵树,如图2。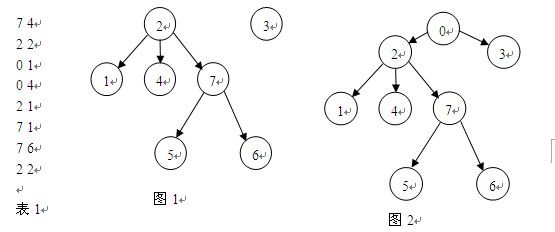
![]()
![]()
如果在一个矩形中,边框上的数都是1,其余数都是0,那么我们称这个矩形为0类矩形
形如
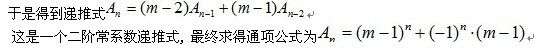

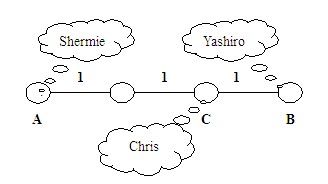
以问题给出的示例为例,将问题抽象成图如下:
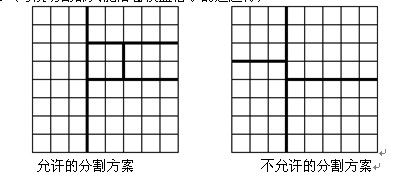

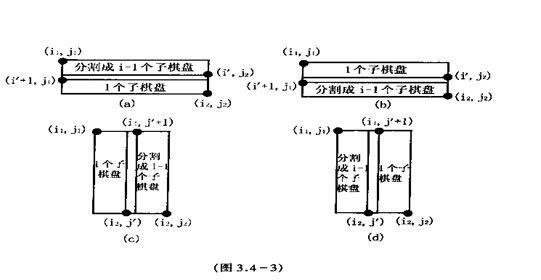
![]()