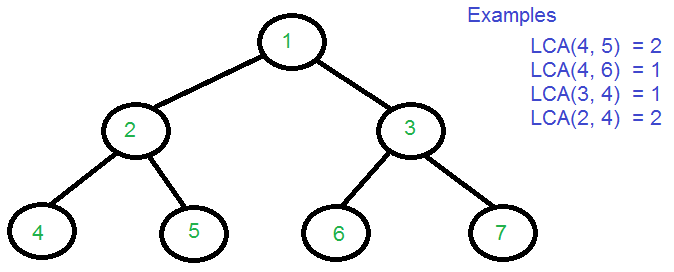
二叉树两个节点的最近公共祖先

转自https://www.geeksforgeeks.org/lowest-common-ancestor-binary-tree-set-1/

Lowest Common Ancestor in a Binary Tree

Given a binary tree (not a binary search tree) and two values say n1 and n2, write a program to find the least common ancestor.

Following is definition of LCA from Wikipedia:
Let T be a rooted tree. The lowest common ancestor between two nodes n1 and n2 is defined as the lowest node in T that has both n1 and n2 as descendants (where we allow a node to be a descendant of itself).

The LCA of n1 and n2 in T is the shared ancestor of n1 and n2 that is located farthest from the root. Computation of lowest common ancestors may be useful, for instance, as part of a procedure for determining the distance between pairs of nodes in a tree: the distance from n1 to n2 can be computed as the distance from the root to n1, plus the distance from the root to n2, minus twice the distance from the root to their lowest common ancestor. (Source Wiki)

Recommended: Please solve it on “PRACTICE” first, before moving on to the solution.

Following are different approaches to find LCA in Binary Tree.

Method 1 (By Storing root to n1 and root to n2 paths):
Following is simple O(n) algorithm to find LCA of n1 and n2.
1) Find path from root to n1 and store it in a vector or array.  找到从root到n1的路径存入向量或数组
2) Find path from root to n2 and store it in another vector or array. 找到从root到n2的路径存入向量或数组
3) Traverse both paths till the values in arrays are same. Return the common element just before the mismatch. 遍历两调路经，返回最早出现的不匹配的前面的公共元素

Following is the implementation of above algorithm.

• // A O(n) solution to find LCA of two given values n1 and n2 #include #include using namespace std;   // A Bianry Tree node struct Node {     int key;     struct Node *left, *right; };   // Utility function creates a new binary tree node with given key Node * newNode(int k) {     Node *temp = new Node;     temp->key = k;     temp->left = temp->right = NULL;     return temp; }   // Finds the path from root node to given root of the tree, Stores the // path in a vector path[], returns true if path exists otherwise false bool findPath(Node *root, vector<int> &path, int k) {     // base case     if (root == NULL) return false;       // Store this node in path vector. The node will be removed if     // not in path from root to k     path.push_back(root->key);       // See if the k is same as root's key     if (root->key == k)         return true;       // Check if k is found in left or right sub-tree     if ( (root->left && findPath(root->left, path, k)) ||          (root->right && findPath(root->right, path, k)) )         return true;       // If not present in subtree rooted with root, remove root from     // path[] and return false     path.pop_back();     return false; }   // Returns LCA if node n1, n2 are present in the given binary tree, // otherwise return -1 int findLCA(Node *root, int n1, int n2) {     // to store paths to n1 and n2 from the root     vector<int> path1, path2;       // Find paths from root to n1 and root to n1. If either n1 or n2     // is not present, return -1     if ( !findPath(root, path1, n1) || !findPath(root, path2, n2))           return -1;       /* Compare the paths to get the first different value */     int i;     for (i = 0; i < path1.size() && i < path2.size() ; i++)         if (path1[i] != path2[i])             break;     return path1[i-1]; }   // Driver program to test above functions int main() {     // Let us create the Binary Tree shown in above diagram.     Node * root = newNode(1);     root->left = newNode(2);     root->right = newNode(3);     root->left->left = newNode(4);     root->left->right = newNode(5);     root->right->left = newNode(6);     root->right->right = newNode(7);     cout << "LCA(4, 5) = " << findLCA(root, 4, 5);     cout << "nLCA(4, 6) = " << findLCA(root, 4, 6);     cout << "nLCA(3, 4) = " << findLCA(root, 3, 4);     cout << "nLCA(2, 4) = " << findLCA(root, 2, 4);     return 0; }

Run on IDE

Output:

 

LCA(4, 5) = 2
LCA(4, 6) = 1
LCA(3, 4) = 1
LCA(2, 4) = 2 

Time Complexity: Time complexity of the above solution is O(n). The tree is traversed twice, and then path arrays are compared.
Thanks to Ravi Chandra Enaganti for suggesting the initial solution based on this method.

Method 2 (Using Single Traversal)
The method 1 finds LCA in O(n) time, but requires three tree traversals plus extra spaces for path arrays. If we assume that the keys n1 and n2 are present in Binary Tree, we can find LCA using single traversal of Binary Tree and without extra storage for path arrays.
The idea is to traverse the tree starting from root. If any of the given keys (n1 and n2) matches with root, then root is LCA (assuming that both keys are present). If root doesn’t match with any of the keys, we recur for left and right subtree. The node which has one key present in its left subtree and the other key present in right subtree is the LCA. If both keys lie in left subtree, then left subtree has LCA also, otherwise LCA lies in right subtree.

•  

/* Program to find LCA of n1 and n2 using one traversal of Binary Tree */ #include using namespace std;   // A Binary Tree Node struct Node {     struct Node *left, *right;     int key; };   // Utility function to create a new tree Node Node* newNode(int key) {     Node *temp = new Node;     temp->key = key;     temp->left = temp->right = NULL;     return temp; }   // This function returns pointer to LCA of two given values n1 and n2. // This function assumes that n1 and n2 are present in Binary Tree struct Node *findLCA(struct Node* root, int n1, int n2) {     // Base case     if (root == NULL) return NULL;       // If either n1 or n2 matches with root's key, report     // the presence by returning root (Note that if a key is     // ancestor of other, then the ancestor key becomes LCA     if (root->key == n1 || root->key == n2)         return root;       // Look for keys in left and right subtrees     Node *left_lca  = findLCA(root->left, n1, n2);     Node *right_lca = findLCA(root->right, n1, n2);       // If both of the above calls return Non-NULL, then one key     // is present in once subtree and other is present in other,     // So this node is the LCA     if (left_lca && right_lca)  return root;       // Otherwise check if left subtree or right subtree is LCA     return (left_lca != NULL)? left_lca: right_lca; }   // Driver program to test above functions int main() {     // Let us create binary tree given in the above example     Node * root = newNode(1);     root->left = newNode(2);     root->right = newNode(3);     root->left->left = newNode(4);     root->left->right = newNode(5);     root->right->left = newNode(6);     root->right->right = newNode(7);     cout << "LCA(4, 5) = " << findLCA(root, 4, 5)->key;     cout << "nLCA(4, 6) = " << findLCA(root, 4, 6)->key;     cout << "nLCA(3, 4) = " << findLCA(root, 3, 4)->key;     cout << "nLCA(2, 4) = " << findLCA(root, 2, 4)->key;     return 0; }

Run on IDE

Output:

 

LCA(4, 5) = 2
LCA(4, 6) = 1
LCA(3, 4) = 1
LCA(2, 4) = 2 

Thanks to Atul Singh for suggesting this solution.

Time Complexity: Time complexity of the above solution is O(n) as the method does a simple tree traversal in bottom up fashion.
Note that the above method assumes that keys are present in Binary Tree. If one key is present and other is absent, then it returns the present key as LCA (Ideally should have returned NULL).
We can extend this method to handle all cases by passing two boolean variables v1 and v2. v1 is set as true when n1 is present in tree and v2 is set as true if n2 is present in tree.

 

/* Program to find LCA of n1 and n2 using one traversal of Binary Tree.    It handles all cases even when n1 or n2 is not there in Binary Tree */ #include using namespace std;   // A Binary Tree Node struct Node {     struct Node *left, *right;     int key; };   // Utility function to create a new tree Node Node* newNode(int key) {     Node *temp = new Node;     temp->key = key;     temp->left = temp->right = NULL;     return temp; }   // This function returns pointer to LCA of two given values n1 and n2. // v1 is set as true by this function if n1 is found // v2 is set as true by this function if n2 is found struct Node *findLCAUtil(struct Node* root, int n1, int n2, bool &v1, bool &v2) {     // Base case     if (root == NULL) return NULL;       // If either n1 or n2 matches with root's key, report the presence     // by setting v1 or v2 as true and return root (Note that if a key     // is ancestor of other, then the ancestor key becomes LCA)     if (root->key == n1)     {         v1 = true;         return root;     }     if (root->key == n2)     {         v2 = true;         return root;     }       // Look for keys in left and right subtrees     Node *left_lca  = findLCAUtil(root->left, n1, n2, v1, v2);     Node *right_lca = findLCAUtil(root->right, n1, n2, v1, v2);       // If both of the above calls return Non-NULL, then one key     // is present in once subtree and other is present in other,     // So this node is the LCA     if (left_lca && right_lca)  return root;       // Otherwise check if left subtree or right subtree is LCA     return (left_lca != NULL)? left_lca: right_lca; }   // Returns true if key k is present in tree rooted with root bool find(Node *root, int k) {     // Base Case     if (root == NULL)         return false;       // If key is present at root, or in left subtree or right subtree,     // return true;     if (root->key == k || find(root->left, k) ||  find(root->right, k))         return true;       // Else return false     return false; }   // This function returns LCA of n1 and n2 only if both n1 and n2 are present // in tree, otherwise returns NULL; Node *findLCA(Node *root, int n1, int n2) {     // Initialize n1 and n2 as not visited     bool v1 = false, v2 = false;       // Find lca of n1 and n2 using the technique discussed above     Node *lca = findLCAUtil(root, n1, n2, v1, v2);       // Return LCA only if both n1 and n2 are present in tree     if (v1 && v2 || v1 && find(lca, n2) || v2 && find(lca, n1))         return lca;       // Else return NULL     return NULL; }   // Driver program to test above functions int main() {     // Let us create binary tree given in the above example     Node * root = newNode(1);     root->left = newNode(2);     root->right = newNode(3);     root->left->left = newNode(4);     root->left->right = newNode(5);     root->right->left = newNode(6);     root->right->right = newNode(7);     Node *lca =  findLCA(root, 4, 5);     if (lca != NULL)        cout << "LCA(4, 5) = " << lca->key;     else        cout << "Keys are not present ";       lca =  findLCA(root, 4, 10);     if (lca != NULL)        cout << "nLCA(4, 10) = " << lca->key;     else        cout << "nKeys are not present ";       return 0; }

Run on IDE

Output:

 

LCA(4, 5) = 2
Keys are not present