SNN系列|神经元模型篇(1) Hodgkin Huxley
Hodgkin Huxley Model
参考
[1] Neuron Dynamics
[2] Spiking Neurons
[3] The Hodgkin Huxley Model
[4] 动作电位的形成机制
[5] 霍奇金赫胥黎枪乌贼巨型轴突
- 1952年发表,1963年获诺贝尔生理学奖
通过对乌贼的巨型轴突进行实验,运用数学方法分析以及三种离子描述了细胞膜电势的动态变化,是其他简化神经元模型的基础。

为什么选择乌贼的巨型轴突呢?
鱿鱼巨型轴突以其异常大的直(〜0.5毫米)而著称。 鱿鱼神经系统和其他神经系统中的大多数轴突通常至少薄100倍。 鱿鱼巨型轴突的大尺寸是一种专门用于迅速传导动作电位的动作电位,当其从掠食者逃脱时会触发鱿鱼的地幔收缩。 除了对鱿鱼有益之外,大直径轴突对实验也有利,因为它允许进行迄今为止在生物物理研究中使用的较小轴突在技术上不可行的操纵。
细胞膜两侧离子浓度差是产生了电势差,在神经元动力学中有重要作用。
-
电势差导致离子浓度差,离子浓度差产生电势差(奈奎斯特电势) Δ u = K t q ln n 1 n 2 \Delta u = \frac{Kt}{q} \ln \frac{n_1}{n_2} Δu=qKtlnn2n1,其中 n 1 n_1 n1为膜外离子浓度, n 2 n_2 n2为膜内离子浓度。
-
反电势:当电势差小于 E N a E_{Na} ENa时,钠离子进入,减小这个差异;反之,当电势差大于 E N a E_{Na} ENa时,钠离子流出,减小这个差异。即当 Δ u \Delta u Δu从 E N a E_{Na} ENa开始变化时,电流的方向就与其变化方向相反,使得其重新回到平衡电势,又称反电势。
这里解释一下为什么膜内钾离子浓度高,而其平衡电势确实膜外为正:因为每个钾离子携带一个正电荷,当钾离子通过通道离开细胞时,同时带出了正电荷,把与其配对的负电荷留在膜内.。正负电荷在空间上分离,不就会产生电场吗?电荷是同性相斥,异性相吸。这个横跨细胞膜的电场会形成一种阻止钾离子外流的力场。 随着钾离子不断流出,电荷在细胞膜两侧不断积累。阻止钾离子外流的力场也不断增加,很快达到与驱动离子外流的扩散力势均力敌,钾离子外流就会停止。
- 静息电位 u r e s t ≈ − 65 m V u_{rest} \approx -65mV urest≈−65mV
HH Model
对巨型章鱼轴突进行实验,主要考察钠、钾和漏(以 c l − cl^- cl−为代表)三种通道。
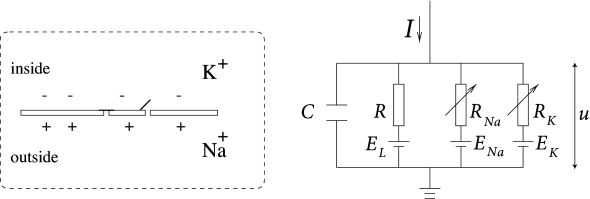
通过实验,Hodgkin和Huxley发现这三个通道的并行关系(控制变量进行实验),宏观电流可以被认为是大量嵌入在细胞膜上的微观离子通道综合作用引起的,所以有了上面的等效电路图,外界电流(电荷)的通路有四条:一条用于给电容充电,另外三条用于流过电阻器。
- 细胞膜是一个半透膜,将膜内外液体分离,它能够存储电荷,起到了电容的作用,记作 C C C
- 钠钾离子通道可以通过电流,其允许离子通过的能力可以用电阻 R N a R_{Na} RNa、 R K R_{K} RK,或电导 g g g表示(为了表达的简便), g = 1 / R g=1/R g=1/R,或者说离子流过的每一个状态都对应一个电阻,因为细胞膜是有对应的离子泵,其通过相应离子的能力可以改变,因此是一个可变电阻器
- 因为细胞膜内外离子浓度不同,与之构建起的平衡的每种离子的电场也不同,根据奈奎斯特公式,每个离子对应一个平衡电势,用 E N a E_{Na} ENa、 E K E_{K} EK表示
- 对于Leaky通道,以 c l − cl^- cl−为代表,其等效为 R R R,为常数,平衡电势用 E L E_L EL表示,该通道的电流相较而言较小
根据电学公式 C = q U C=qU C=qU、 I C = C d u d t I_C=C\frac{du}{dt} IC=Cdtdu以及并联电流公式,可得
I ( t ) = I C ( t ) + ∑ k I k ( t ) + I L ( t ) C d u d t = − ∑ k I k ( t ) + I ( t ) I(t) = I_C(t) + \sum \limits_k I_k(t) + I_L(t)\\ C\frac{du}{dt} = -\sum\limits_k I_k(t) + I(t) I(t)=IC(t)+k∑Ik(t)+IL(t)Cdtdu=−k∑Ik(t)+I(t)
式中, ∑ k I k \sum\limits_kI_k k∑Ik表示通过细胞膜的离子电流的和,例如对漏通道,考虑到平衡电势, I L = g L ( u − E L ) I_L = g_L(u-E_L) IL=gL(u−EL)。
关于 I I I的方向问题:惯例是电流由膜内流向膜外为正。
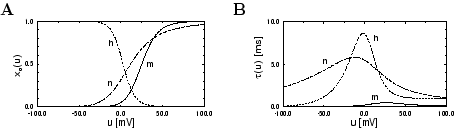
平衡电势 E E E可测,膜电势 u u u以及电流 I I I都可以测量,但各离子通道的电导 g g g该如何测量呢?Hodgkin和Huxley成功测量了各通道的电阻(电导)是如何随时间和膜电势变化的,他们引入门控变量 m m m, n n n, h h h来对给定时间通道开启的概率进行建模,得出如下关系式。这里 m m m和 n n n共同负责调控 N a Na Na离子通道, h h h负责调控 K K K离子通道。 m m m, n n n, h h h是根据相应的时间常数不断变化的。
动作电位的形成
到这里,谈一下动作电位的形成过程:静息状态时, N a Na Na离子激活态门处于关闭状态而失活态门处于开放状态,细胞膜受刺激时对 N a Na Na离子的通透性增加,即去极化阶段,表现在 N a Na Na离子的两个门都处于开放阶段,当膜电势达到阈值时,膜对 N a Na Na离子的通透性显著增加,膜电位迅速由负变正接近Na离子的平衡电位,但未真正达到,此时 N a Na Na离子失活态门开始关闭,Na离子的通透性开始下降到静息水平,K离子的通道门缓慢开放,导致动作电位从峰值返回到静息状态水平,称为再极化,变化的膜电势时 N a Na Na离子通道完全关闭,由于 K K K离子通道关闭的速度较慢,使得稍微过量的 K K K离子流出使得细胞膜电势比静息电位还低,形成超极化电位。
可见, N a Na Na离子的流通与两个门有关,也就是 m m m和 h h h, K K K离子的流通与一个门有关,也就是 n n n。
门控变量
每个离子通道都有两种状态,允许和不允许状态(permissive or non-permissive)。用 p i ( t ) p_i(t) pi(t)表示某离子通道某时刻的概率,值的大小从0到1变化,由不允许到允许转换的速率为 α i ( t ) \alpha_i(t) αi(t),由允许到不允许状态转换的速率为 β i ( t ) \beta_i(t) βi(t)。于是对打开概率进行建模为 d p i d t = α i ( u ) ( 1 − p i ) + β i ( u ) p i \frac{dp_i}{dt} = \alpha_i(u)(1-p_i) + \beta_i(u)p_i dtdpi=αi(u)(1−pi)+βi(u)pi。当某个离子通道打开后,相应的宏观电流也发生变化,因此有 G k = g k ∏ i p i G_k = g_k \prod \limits _i p_i Gk=gki∏pi,其中 g k g_k gk表示当所有离子通道打开时的归一化系数。
d m d t = α m ( u ) ( 1 − m ) + β m ( u ) m d h d t = α h ( u ) ( 1 − h ) + β h ( u ) h d n d t = α n ( u ) ( 1 − n ) + β n ( u ) n \frac{dm}{dt}=\alpha_m(u)(1-m) + \beta_m(u)m\\ \frac{dh}{dt}=\alpha_h(u)(1-h) + \beta_h(u)h\\ \frac{dn}{dt}=\alpha_n(u)(1-n) + \beta_n(u)n dtdm=αm(u)(1−m)+βm(u)mdtdh=αh(u)(1−h)+βh(u)hdtdn=αn(u)(1−n)+βn(u)n
允许与不允许状态转换速率是与膜电势有关的,实验测得六个参数分别是
| x x x | α x ( u / m V ) \alpha_x(u/mV) αx(u/mV) | β x ( u / m V ) \beta_x(u/mV) βx(u/mV) |
|---|---|---|
| n n n | ( 0.1 − 0.01 u ) / [ exp ( 1 − 0.1 u ) − 1 ] (0.1-0.01u)/[\exp(1-0.1u)-1] (0.1−0.01u)/[exp(1−0.1u)−1] | 0.125 exp ( − u / 80 ) 0.125\exp(-u/80) 0.125exp(−u/80) |
| m m m | ( 2.5 − 0.1 u ) / [ exp ( 2.5 − 0.1 u ) − 1 ] (2.5-0.1u)/[\exp(2.5-0.1u)-1] (2.5−0.1u)/[exp(2.5−0.1u)−1] | 4 exp ( − u / 18 ) 4\exp(-u/18) 4exp(−u/18) |
| h h h | 0.07 exp ( − u / 20 ) 0.07\exp(-u/20) 0.07exp(−u/20) | 1 / [ exp ( 3 − 0.1 u ) + 1 ] 1/[\exp(3-0.1u)+1] 1/[exp(3−0.1u)+1] |
初始化时, x 0 = α i / ( α i + β i ) x_0 = \alpha_i / (\alpha_i+\beta_i) x0=αi/(αi+βi)
综上,离子通道的电流之和可以用下式表述:
∑ k I k = g N a m 3 h ( u − E N a ) + g K n 4 ( u − E K ) + g L ( u − E L ) \sum\limits_k I_k=g_{Na}m^3h(u-E_{Na}) + g_Kn^4(u-E_K) + g_L(u-E_L) k∑Ik=gNam3h(u−ENa)+gKn4(u−EK)+gL(u−EL)
通过上述公式,我们可以对膜电势进行建模,使用恒定电流刺激,仿真结果如下:
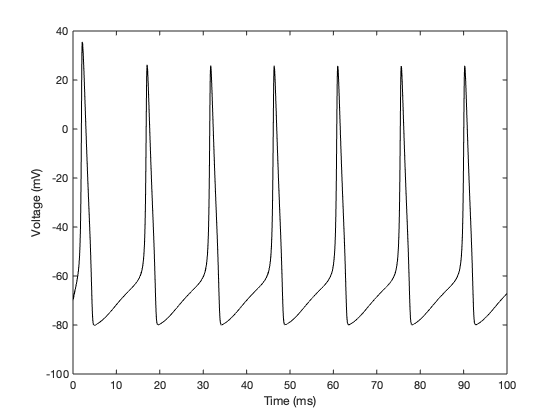
上图为单脉冲,当恒定输入很强时,神经元会产生脉冲序列,如下图所示:
脉冲发放率
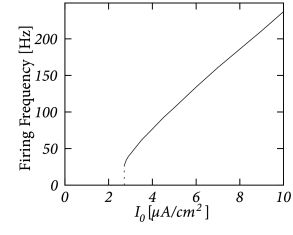
可以发现,在某强度下恒定电流刺激时,神经元发放一定数量的脉冲,则单位时间下神经元的脉冲发放数量即为脉冲发放率。对各电流强度下进行实验,即可得到F-I图:
- 激活阈值:当神经元膜电势超过阈值,神经元发放脉冲
当刺激电流比较小的时候,神经元不会发放脉冲信号,其膜电势会不断leaky,直到回落到静息电位。那么这能说明存在一个电流阈值使得其刺激神经元时介于发放与不发放之间吗?我们做一个实验,首先实验一个电流强度和持续刺激时间合适,使得神经元不发放脉冲(比放好不发放脉冲的程度小一点),然后将电流强度提升一倍,刺激时间减小一倍,再去刺激神经元发现结果和之前一样,这说明不是电流强度决定是否发放脉冲,而是累计的电荷量,也就是膜电势阈值决定脉冲发放。但这在HH模型中并未显式提出。
问题来了,是不是当电流强到一定程度,脉冲发放率会无穷的大?这就要提到动作电位的不应期(Refractory)。
- 不应期:大多数 Na+ 通道失活时被称为绝对不应期
神经元动作电位先后经过去极化、再极化、超极化阶段,有峰值电位回落时回到比静息电位还要低,此时离子泵要经过调整才能回到静息状态,准备再次发放脉冲,也就是说,在不应期中,无论加多大刺激,神经元都不会再发放脉冲了。
MATLAB实现
具体步骤如下:
1、设置参数,包括平衡电势、电容、电阻、静息电位、最大电导、dt、以及仿真时长
2、循环开始
更新 α \alpha α β \beta β
若i为1,利用上述参数得到初始化mnh
根据mnh更新电导
计算各通道电流,得到 − ∑ k I k ( t ) + I ( t ) -\sum\limits_k I_k(t) + I(t) −k∑Ik(t)+I(t)
更新膜电势
根据膜电势更新mnh
%this a Matlab implement of HH Model
%=======================================
% Function name: run_model
% Inputs (2): -I_inj, the injection current array in uA/cm^2
% -dt, the time step in ms
%
% Function description:
% This function runs the Hodgkin Huxley model for a given injection current
% and time step over 100 ms. The membrane voltage, K+ conductance, and Na+
% conductance are plotted afterwards.
%=======================================
function run_model(I_inj, dt)
global num_spike
num_spike = 0;
% Initialize time vector and time step
t = 0:dt:100; %Time (ms)
% Initialize m, n, and h, which represent K+ channel activation, Na+
% channel activation, and Na+ channel inactivation, respectively.
m = zeros(1, length(t));
n = zeros(1, length(t));
h = zeros(1, length(t));
% Initialize alphas and betas, the rate constants
alpha_m = zeros(1,length(t));
beta_m = zeros(1,length(t));
alpha_n = zeros(1,length(t));
beta_n = zeros(1,length(t));
alpha_h = zeros(1,length(t));
beta_h = zeros(1,length(t));
% Initialize membrane voltage and conductance vectors
V_m = zeros(1,length(t));
g_K = zeros(1,length(t));
g_Na = zeros(1, length(t));
% Constants
g_K_max = 36; %K+ channel max conductance (mS/cm^2)
g_Na_max = 120; %Na+ channel max conductance (mS/cm^2)
g_L = 0.3; %Leakage current conductance (mS/cm^2)
E_K = -12; %K+ channel Nernst potential (mV)
E_Na = 115; %Na+ channel Nernst potential (mV)
E_L = 10.6; %Leakage channel Nernst potential (mV)
V_rest = -70; %Resting voltage (mV)
C_m = 1.0; %Membrance capacitance (uF/cm^2)
for i = 1:(length(t)-1)
% V_m(1) = 60;
% Calculate all alpha and beta values
alpha_m(i) = 0.1*((25 - V_m(i))/(exp((25-V_m(i))/10)-1));
beta_m(i) = 4*exp(-1*V_m(i)/18);
alpha_n(i) = 0.01*((10-V_m(i))/(exp((10-V_m(i))/10)-1));
beta_n(i) = 0.125*exp(-1*V_m(i)/80);
alpha_h(i) = 0.07*exp(-1*V_m(i)/20);
beta_h(i) = 1/(exp((30-V_m(i))/10)+1);
% Initial conditions
if(i == 1)
m(i) = alpha_m(i)/(alpha_m(i) + beta_m(i));
n(i) = alpha_n(i)/(alpha_n(i) + beta_n(i));
h(i) = alpha_h(i)/(alpha_h(i) + beta_h(i));
end
% Calculate conductances
g_Na(i) = m(i)^3*g_Na_max*h(i);
g_K(i) = n(i)^4*g_K_max;
% Calculate currents
I_Na = g_Na(i)*(V_m(i) - E_Na);
I_K = g_K(i)*(V_m(i) - E_K);
I_L = g_L*(V_m(i) - E_L);
I_ion = I_inj(i) - I_K - I_Na - I_L;
% Calculate membrane voltage, m, n, and h using Euler's method
V_m(i+1) = V_m(i) + I_ion/C_m*dt;
m(i+1) = m(i) + (alpha_m(i)*(1-m(i))-beta_m(i)*m(i))*dt;
n(i+1) = n(i) + (alpha_n(i)*(1-n(i))-beta_n(i)*n(i))*dt;
h(i+1) = h(i) + (alpha_h(i)*(1-h(i))-beta_h(i)*h(i))*dt;
%check spike
if V_m(i) > 0 - V_rest
if (V_m(i)>V_m(i-1)) && (V_m(i)>V_m(i+1))
num_spike = num_spike + 1;
end
end
end
V_m = V_m + V_rest;
运行结果图如下: