SNN系列|神经元模型篇(2) Izhikevich
Izhikevich Model
参考
[1] IZHIKEVICH QUADRATIC MODEL FOR SPIKING NEURONS
[2] 神经妙算
[3] 原始论文
[4] 快速了解
[5] Izhikevich神经元控制参数对可塑性神经元网络动力学的影响
- Izhikevich博士于2003年提出,使用二叉树对HH数学上的简化
- 对神经元的简化,最简化的是只保留firing rate
- 于HH与LIF之间进行计算复杂与动态性能的权衡
对二次整合神经元的改进:
出发点:
HH神经元无疑是生物可解释性最强的,但参数太多,计算复杂,因此需要基于合理的假设作出比较好的妥协。二次整合神经元相较于整合发放神经元(IF)脉冲不是人为添加,而是靠二次函数短时间内快速上升。
C v ′ = k ( v − v r e s t ) ( v − v t h r e s h ) + I ( t ) i f v ≥ v p e a k , t h e n v ← c Cv^{\prime} = k(v-v_{rest})(v-v_{thresh}) + I(t)\\ if\ v \geq v_{peak},\ \ \ then\ v\leftarrow c Cv′=k(v−vrest)(v−vthresh)+I(t)if v≥vpeak, then v←c
优点:
1、平滑的脉冲生成机制和脉冲的自动上冲
2、硬的峰后自动复位
使用分叉方法将HH模型简化为二阶常微分方程,Izhikevich在上述基础上加入恢复变量,使得神经元具有更加丰富的动态特性,而没有显著提高计算复杂度。
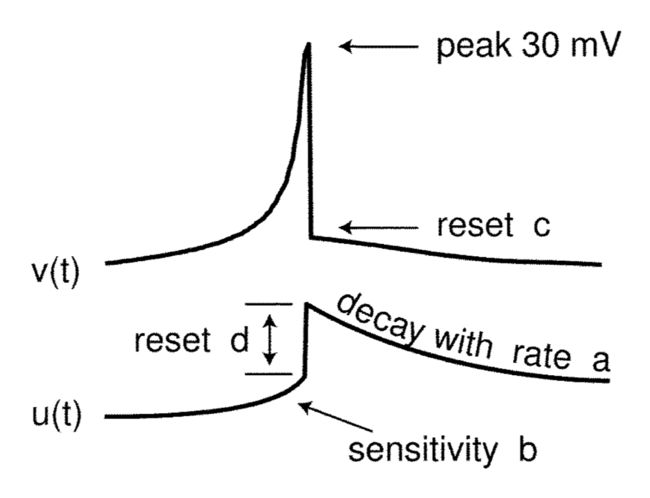
C d v d t = k ( v − v r ) ( v − v t ) − u + S d u d t = a ( b ( v − v r ) − u ) i f v ≥ v p e a k , t h e n v ← c , u ← u + d C\frac{dv}{dt} = k(v-v_r)(v-v_t)-u+S\\ \frac{du}{dt} = a(b(v-v_r)-u)\\ if\ \ v\geq v_{peak}, \ \ then \ \ v \leftarrow c,\ \ u \leftarrow u+d Cdtdv=k(v−vr)(v−vt)−u+Sdtdu=a(b(v−vr)−u)if v≥vpeak, then v←c, u←u+d
各参数意义:
| 参数 | 含义 | 典型值 | 单位 |
|---|---|---|---|
| a | u u u的时间常数,用于膜电势缓慢恢复 | 0.02 | m s − 1 ms^{-1} ms−1 |
| b | u u u对 v v v的依赖程度参数 | 0.2 | 1 0 − 9 Ω − 1 10^{-9}\Omega^{-1} 10−9Ω−1 |
| c | 脉冲后reset的值 | -65mV | m V mV mV |
| d | reset后 u u u增加程度 | 2 | |
| S | 刺激,包括兴奋的、抑制的、内部的、噪声等 | p A p A pA | |
| v | 膜电势 | m V m V mV | |
| u | 恢复变量 | p A pA pA | |
| vt | 瞬时阈值电位 | m V mV mV | |
| vr | 静息电位 | m V m V mV |
u是膜电位恢复变量,主要用于统计火花钾离子和钝化钠离子的流动规律,并对膜电位起负反馈作用。
每个参数对神经元的动态性能都是有影响的(可以进行实验仿真)
- 在一定范围内,恢复变量的时间尺度参数的存在一个能够决定网络放电节律中 γ \gamma γ节律是否存在的临界值;此外时间尺度参数的变化会影响 γ \gamma γ节律出现的时间
- 恢复变量对膜电位的依赖程度参数能够影响可塑性网络的放电行为,低依赖程度参数下的网络,可能会出现体现无标度性质的“单神经元放电”放电行为
简化模型:
p ′ = 0.04 v 2 + 5 v + 140 − u + I u ′ = a ( b v − u ) i f v > 30 m V , t h e n v ← c , u ← u + d p^\prime = 0.04v^2+5v+140-u+I\\ u^\prime = a(bv-u)\\ if \ \ v>30mV, \ \ then \ \ \ v\leftarrow c,\ \ \ u\leftarrow u+d p′=0.04v2+5v+140−u+Iu′=a(bv−u)if v>30mV, then v←c, u←u+d
- 0.04 v 2 + 5 v + 140 0.04v^2+5v+140 0.04v2+5v+140的取值是为了将膜电势限制在mv水平,时间限制在ms水平,选用其他参数亦可
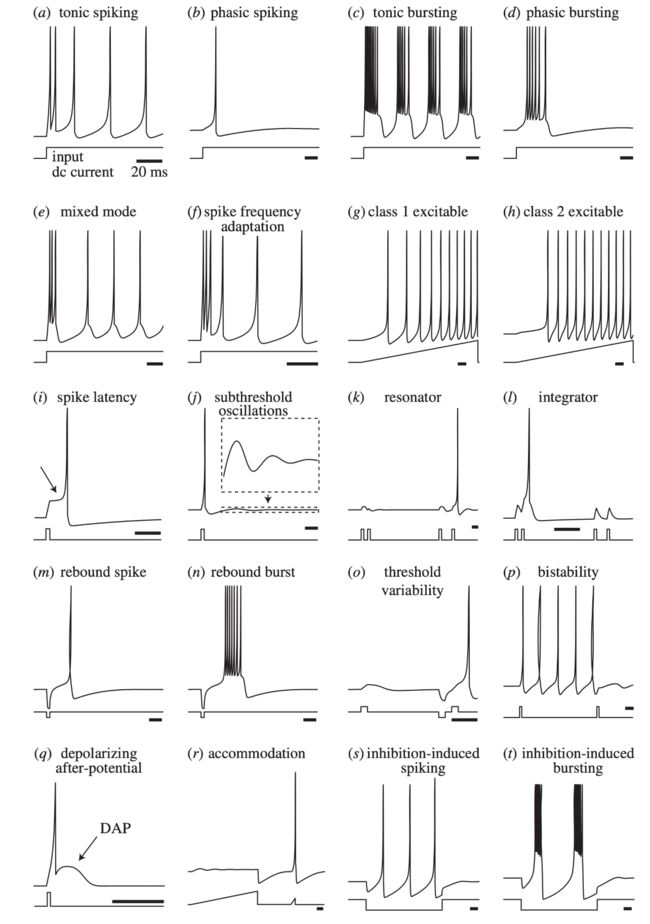
动态特性
能模拟丰富的脉冲形式,同时具有很高的计算性能。
在不同的参数下,Izhikevich神经元能够产生不同频率的电波,进而通过神经元的同步放电在可塑性网络中形成不同的放电节律,因此非常适合于大型网络的仿真。
Matlab代码
四个参数定天下
%Created by Eugene M. Izhikevich, February 25, 2003
% Excitatory neurons Inhibitory neurons
Ne=800;
Ni=200;
re=rand(Ne,1);
ri=rand(Ni,1);
a=[0.02*ones(Ne,1); 0.02+0.08*ri];
b=[0.2*ones(Ne,1); 0.25-0.05*ri];
c=[-65+15*re.^2; -65*ones(Ni,1)];
d=[8-6*re.^2; 2*ones(Ni,1)];
S=[0.5*rand(Ne+Ni,Ne), -rand(Ne+Ni,Ni)];
v=-65*ones(Ne+Ni,1); % Initial values of v
u=b.*v; % Initial values of u
firings=[]; % spike timings
for t=1:1000 % simulation of 1000 ms
I=[5*randn(Ne,1);2*randn(Ni,1)]; % thalamic input
fired=find(v>=30); % indices of spikes
firings=[firings; t+0*fired,fired];
v(fired)=c(fired);
u(fired)=u(fired)+d(fired);
I=I+sum(S(:,fired),2);
v=v+0.5*(0.04*v.^2+5*v+140-u+I); % step 0.5 ms
v=v+0.5*(0.04*v.^2+5*v+140-u+I); % for numerical
u=u+a.*(b.*v-u); % stability
end
plot(firings(:,1),firings(:,2),'.');