SNN系列|神经元模型篇(4) LIF
Leaky Intergrate and Fired Model
参考:
[1] Neuron Dynamics
[2] 早期的公众号
引言
SNN与ANN最主要的不同就是使用离散的脉冲信号替代ANN网络中传播的连续的模拟信号。为了在这种网络结构上产生脉冲信号,SNN使用了更加复杂也更加贴近于生物的神经元模型,目前使用最多的是**Leakyintegrity-Fire(LIF)**模型。对于这类神经元模型来说,输入信号直接影响的是神经元的状态(膜电位),只有当膜电位上升到阈值电位时,才会产生输出脉冲信号。
该模型利用给定神经元的神经元动作电位总是具有大致相同的形式这一事实。如果动作电位的形状总是相同的,那么这个形状就不能用来传递信息:而是包含在有或没有尖峰的情况下。因此,动作电位被还原为发生在精确时刻的“事件”。
一些基本概念
更详细的脉冲发放机制可以参考另一篇博文
-
膜电势:细胞膜两侧的电位差,在神经细胞通讯中起到重要作用。当膜电势超过阈值时发放脉冲
-
静息电位:神经元处于极化状态,是细胞膜电位的常态
-
动作电位:细胞接收外界刺激,细胞膜两侧离子快速跨膜运动,引起膜电位变化
-
超极化:是指跨膜电位处于较原来的参照状态(如静息状态)下的跨膜电位更负(膜电位的绝对值更高)的状态。
-
去极化:去极化是指跨膜电位处于较原来的参照状态下的跨膜电位更正(膜电位的绝对值较低)的状态。
模型描述
Leaky指泄露,表示如果神经元输入只有一个时,不足以让膜电势超过阈值,由于细胞膜不断进行膜内外离子交换,膜电势会自动发生泄露逐渐回落到静息状态;
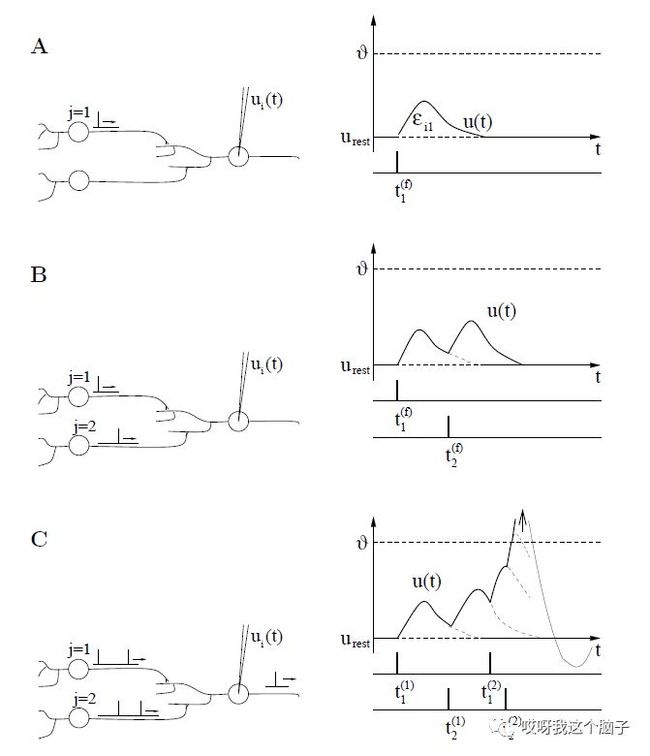
Integrate指积分,表示神经元会接收所有与该神经元相连的轴突末端(上一个神经元)到来的脉冲;
Fire指激发,表示当膜电势超过阈值时,神经元会发送脉冲。神经元发送脉冲后会进入超极化状态,然后是不应期(Refractory Period),在不应期内即使给予刺激也不会反应,即神经元不再接收刺激,保持静息电位。
所以LIF模型的任务就是建模膜电势随时间以及外界输入的变化情况。为了方便解释LIF神经元模型中的一些变量,可以查看HH模型。
Leaky Integrate and Fire neurons简称LIF模型,是一种对HH模型的最基础的简化。但不是单纯的省略变量。该模型不去刻意的描述动作电位的形状。为了得到瞬时电压与输入电流的关系,使用电学理论的基本理论来解释该问题。一个神经元被细胞膜包围,细胞膜是很好的绝缘体。如果想神经元注射电流,那么附加的电荷
q = ∫ I ( t ) d t q = \int I(t) \mathrm{d}t q=∫I(t)dt
必须到达一个地方:它会给细胞膜充电。因此,细胞膜就像一个电容器。因为绝缘体不完美,所以随着时间的推移,电荷会慢慢地从细胞膜漏出,因此细胞膜可以用有限的泄露电阻表示。基本的表示LIF模型的电回路由电容 C C C和一个由 I I I驱动的电阻 R R R并联而成。

如果驱动电流消失,则整个电容器的电压由 U r e s U_{res} Ures提供。为了分析电路,我们利用电流守恒定律,将驱动电流分成两部分:
I ( t ) = I R + I C I(t)=I_{R}+I_{C} I(t)=IR+IC
第二个分量是给电容器充电,因此流过电容的电流 R = C d u d t R = C\frac{\mathrm{d} u}{\mathrm{d}t} R=Cdtdu:
I ( t ) = u ( t ) − u r e s R + C d u ( t ) d t I(t)=\frac{u(t)-u_{r e s}}{R}+C \frac{d u(t)}{d t} I(t)=Ru(t)−ures+Cdtdu(t)
引入时间常数 τ m = R C \tau_m = RC τm=RC,则有:
τ m d u ( t ) d t = − ( u ( t ) − u r e s ) + R I ( t ) \tau_{m} \frac{d u(t)}{d t}=-\left(u(t)-u_{r e s}\right)+R I(t) τmdtdu(t)=−(u(t)−ures)+RI(t)
下面来讨论一下方程的解,假设时间为0时,膜电势取 U r e s + Δ u U_{res}+\Delta u Ures+Δu。以后的时间输入电流都为0,直觉上,如果有足够的时间,膜电位会放松到静息电位,解方程得
u ( t ) − u r e s = Δ u exp ( − t − t 0 τ m ) for t > t 0 u(t)-u_{r e s}=\Delta u \exp \left(-\frac{t-t_{0}}{\tau_{m}}\right) \quad \text { for } \quad t>t_{0} u(t)−ures=Δuexp(−τmt−t0) for t>t0
因此,在没有输入的情况下,膜电位会指数衰减到静息电位。时间常数是衰减的特征时间。对于一个典型神经元来说,它在10ms范围内,一次相对于1ms的脉冲的持续时间来说足够长。
当有输入电流时,初始时电压为静息电位,则方程的解是:
u ( t ) = − u r e s + R I 0 Δ u [ 1 − exp ( − t τ ) ] u(t)=-u_{r e s}+R I_{0} \Delta u\left[1-\exp \left(-\frac{t}{\tau}\right)\right] u(t)=−ures+RI0Δu[1−exp(−τt)]

LIF模型
因此,LIF模型由两部组成:
Leaky intergration: τ m d u d t = − [ u ( t ) − u r e s t ] + R I ( t ) Reset : lim δ → 0 ; δ > 0 u ( t ( f ) + δ ) = u r \begin{array}{l}{\text { Leaky intergration: } \tau_{m} \frac{\mathrm{d} u}{\mathrm{d} t}=-\left[u(t)-u_{\mathrm{rest}}\right]+R I(t)} \\ {\text { Reset }: \lim _{\delta \rightarrow 0 ; \delta>0} u\left(t^{(f)}+\delta\right)=u_{r}}\end{array} Leaky intergration: τmdtdu=−[u(t)−urest]+RI(t) Reset :limδ→0;δ>0u(t(f)+δ)=ur
几个应用:
LIF神经元在表示上有多种形式,以下为两种常见表示方式
- [A Plasticity-Centric Approach to Train the Non-Differential SpikingNeural Networks][https://www.aaai.org/ocs/index.php/AAAI/AAAI18/paper/viewPaper/16105]
τ m d V d t = − ( V − V L ) + g E g L ( V − V E ) τ E d g E d t = − g E + η ∑ j ∈ N E w j , i δ t \tau_{m} \frac{\mathrm{d} V}{\mathrm{d} t}=-\left(V-V_L \right)+ \frac{g_E}{g_L}(V-V_E)\\ \tau_E\frac{\mathrm{d}g_E}{\mathrm{d}t} = -g_E + \eta \sum \limits _{j\in N_E}w_{j,i}\delta_t τmdtdV=−(V−VL)+gLgE(V−VE)τEdtdgE=−gE+ηj∈NE∑wj,iδt
| g L g_L gL | 漏电导 |
|---|---|
| g E g_E gE | 总兴奋电导 |
| V E V_E VE | 反电势 |
| V L V_L VL | 漏电势 |
| τ E \tau_E τE | 兴奋神经元电导延迟 |
参考代码:
gE = gE -gE*dt/tau_syn_E + inputs;
volt = volt -dt/taum*(volt - V_leak*ones(batchsize,n_neuron) + gE/g_leak.*(volt- V_E*ones(batchsize,n_neuron)));
spiking = volt > V_th;
volt(spiking) = V_reset;
- Jointly Learning Network Connections and Link Weights in SpikingNeural Networks
V j ( t ) = ∑ i = 1 N W i , j ∑ t i < t K ( t − t i ) + V rest K ( t − t i ) = V 0 ( exp ( − t − t i τ m ) − exp ( − t − t i τ s ) ) \begin{array}{l}{V_{j}(t)=\sum_{i=1}^{N} W_{i, j} \sum_{t_{i}
| K | 核函数 |
|---|---|
| V 0 V_0 V0 | 使括号内函数最大值为1 |
| τ m \tau_m τm | 膜积分时间延迟常数 |
| τ s \tau_s τs | 突触电流时间延迟常数 |
参考代码:
function response = K(t,t_i)
time = 0:1:100;
Tou_m = 15;
Tou_s = Tou_m/4;
% normalize factor(divided by maximum)
V_0 = 1/( max(exp(-(time)/Tou_m) - exp(-(time)/Tou_s)) );
response=V_0*(exp(-(t-t_i)/Tou_m)-exp(-(t-t_i)/Tou_s))*heavyside(t,t_i);
end
test = InputSpike(101:150,:);
for t = 1:T
for neuron = 1:neurons %% Response function for 48 neurons at time t
Response(neuron) = K(t,test(test_sample,neuron));
end
% Calculate PSP
for j = 1:3
V(j,t) = Response*weight(:,j) + V_rest;
end
end