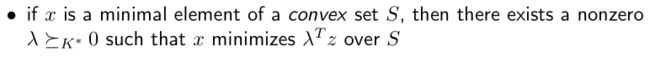Convex Optimization: 2 Convex sets
本篇为凸优化的课程笔记。
文章目录
- Affine set 仿射集
- Convex set 凸集
- Convex combination and convex hull 凸组合与凸包
- Convex cone 凸锥
- Hyperplanes and halfspaces 超平面与半空间
- Euclidean balls and ellipsoids 欧几里得球和椭球
- Norm balls and norm cones 范数球与范数锥
- Polyhedra 多面体
- Positive semidefinite cone 半正定锥
- Operations that preserve convexity 保持凸性的操作
- Intersection 取交
- Affine function 仿射函数
- Perspective and linear-fractional function 透视函数与分式线性函数
- Generalized inequalities 推广的不等式
- Minimum and minimal elements
- Separating hyperplane theorem 分离超平面定理
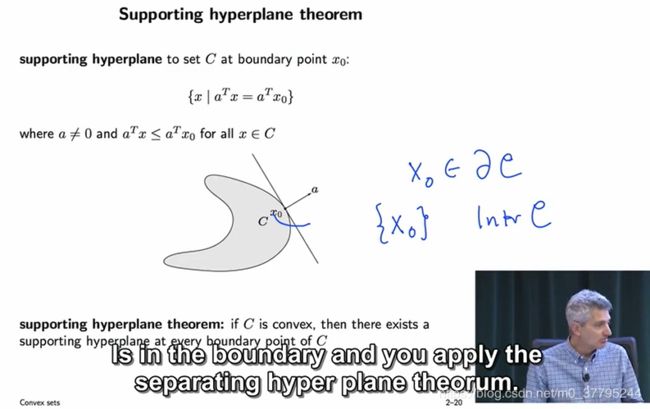
- Supporting hyperplane theorem 支撑超平面定理
- Dual cones and generalized inequalities 对偶锥以及推广不等式
- Minimum and minimal elements via dual inequalities
- optimal production frontier
Affine set 仿射集

过两个点 x 1 , x 2 x_1,x_2 x1,x2 的直线上所有点形成仿射集。
这个例子可以玩味一下:线性方程组 { x ∣ A x = b } \{x|Ax=b\} {x∣Ax=b} 的解集是仿射集,证明如下:
A x 1 = b , A x 2 = b A x = A ( θ x 1 + ( 1 − θ ) x 2 ) = θ A x 1 + ( 1 − θ ) A x 2 = θ b + ( 1 − θ ) b = b \begin{aligned} Ax_1&=b,\ Ax_2=b\\ Ax&=A(\theta x_1+(1-\theta)x_2)\\ &=\theta Ax_1+(1-\theta)Ax_2\\ &=\theta b+(1-\theta)b=b \end{aligned} Ax1Ax=b, Ax2=b=A(θx1+(1−θ)x2)=θAx1+(1−θ)Ax2=θb+(1−θ)b=b
Convex set 凸集
Convex combination and convex hull 凸组合与凸包

凸组合为点的线性组合,其中每个参数要求大于等于零,且参数和为1. 集合 S S S 的凸包则为 S S S 中所有点的凸组合。
Convex cone 凸锥
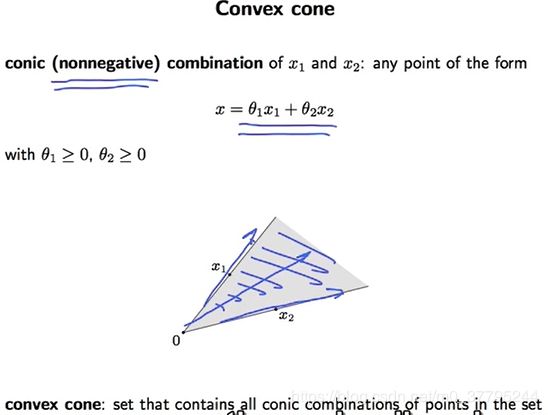
凸锥组合类似凸组合,不同之处在于参数的和没有等于 1 这一限制,但是每个参数仍要大于等于零。凸锥则为集合中所有点的凸锥组合形成的集合。
Hyperplanes and halfspaces 超平面与半空间
Euclidean balls and ellipsoids 欧几里得球和椭球

![]()
欧几里得球是距离中心点的二范数小于 r r r 的点集, r r r 是该球的半径。椭球也有相应的表示。
需要注意的是在椭球的第一种表示中 { x ∣ ( x − x c ) T P − 1 ( x − x c ) ≤ 1 } \{x|(x-x_c)^TP^{-1}(x-x_c)\le1\} {x∣(x−xc)TP−1(x−xc)≤1} 中的 P P P 和集合是一一对应的,也就是说相同集合对应的矩阵 P P P 是唯一的,此处 P P P 是一个对称的正定矩阵。
而在第二种表示中 { x c + A u ∣ ∥ u ∥ 2 ≤ 1 } \{x_c+Au|\|u\|_2\le 1\} {xc+Au∣∥u∥2≤1},此处的矩阵 A A A 不唯一,假如把 A A A 换成 A Q AQ AQ,其中 Q Q Q 是一个正交矩阵,那么这个集合仍然不变,因为相当于是对 u u u 先做了一下旋转。而假如限定矩阵 A A A 必须是一个对称正定矩阵的话, A A A 就变成唯一的了(证明方法是对 A A A 进行奇异值分解)。
Norm balls and norm cones 范数球与范数锥
- 非负性, 只在 x = 0 x=0 x=0 的时候结果才是零
- 齐次性
- 三角不等式
欧几里得范数锥也叫做二阶锥。范数球和范数锥都是凸的。
Polyhedra 多面体
Positive semidefinite cone 半正定锥
Operations that preserve convexity 保持凸性的操作
Intersection 取交

凸集的交集仍是凸集,PPT给的这个例子很妙,见板书里的证明。
Affine function 仿射函数

仿射函数更加一般的说法叫做线性函数。一个凸集经过仿射函数的变换后仍是凸集,反过来也是一样的,凸集经过逆变换之后仍是凸集。注意有可能实际方程的逆变换并不存在,但是凸集经过逆变换之后仍是凸集的这个关系是存在的。
仿射函数的例子有:缩放,平移,投影。
还有双曲锥(hyperbolic cone):
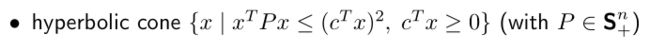
(?什么是双曲锥)
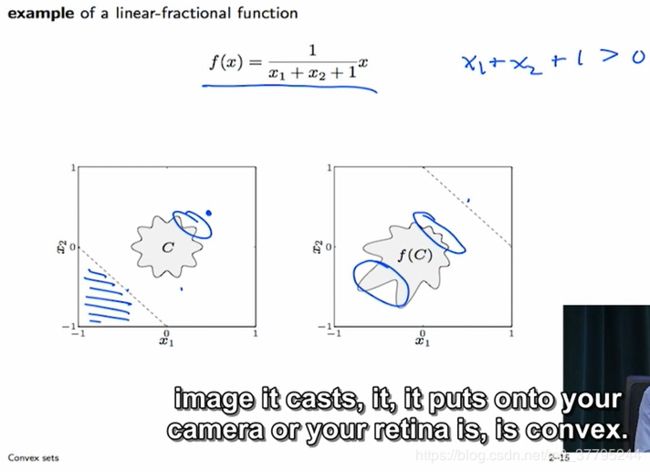
Perspective and linear-fractional function 透视函数与分式线性函数
Generalized inequalities 推广的不等式
一个凸锥 K ⊆ R n K\sube\mathcal{R}^n K⊆Rn,当它满足以下三个条件时,被称作是一个真锥(proper cone):
- K K K 是闭的(closed),即包含边界
- K K K 是实在的(solid), 即其内部是非空的,比如一条射线是一个锥,但是这个射线内部是空的(点都在边界上)
- K K K 是 pointed 的,意思是不包含直线,比如说一条直线(双向延申)是一个锥,但不是一个真锥,也就是说真锥意味着是单向延申的。
举几个栗子:
- 非负象限: K = R + n = { x ∈ R n ∣ x i ≥ 0 , i = 1 , . . . , n } K=\mathcal{R}_+^n=\{x\in\mathcal{R}^n|x_i\ge 0,i=1,...,n\} K=R+n={x∈Rn∣xi≥0,i=1,...,n}
- 半正定锥 K = S + n K=\mathcal{S}_+^n K=S+n
- [ 0 , 1 ] [0,1] [0,1] 上的非负多项式:
K = { x ∈ R n ∣ x 1 + x 2 t + x 3 t 2 + ⋯ + x n t n − 1 ≥ 0 for t ∈ [ 0 , 1 ] } K=\{x\in\mathcal{R}^n|x_1+x_2t+x_3t^2+\cdots+x_nt^{n-1}\ge 0\text{ for }t\in[0,1]\} K={x∈Rn∣x1+x2t+x3t2+⋯+xntn−1≥0 for t∈[0,1]}
generalized inequality 推广不等式:
定义一个真锥 K K K,则:
x ⪯ K y ⟺ y − x ∈ K , x ≺ K y ⟺ y − x ∈ i n t K x\preceq_Ky\iff y-x\in K,\quad x\prec_Ky\iff y-x\in\mathbf{int}K x⪯Ky⟺y−x∈K,x≺Ky⟺y−x∈intK
即 x x x 在真锥 K K K 范围内小于等于 y y y,则说明其差值在真锥范围内;假如是严格小于,则其差值在真锥内部的点中(就是说不在边界上, i n t \mathbf{int} int 表示 interitor)
举几个例子:
- 每个元素的不等式( K = R + n K=\mathcal{R}_+^n K=R+n,即 K K K 是非负实数),则:
x ⪯ R + n y ⟺ x i ≤ y i , i = 1 , . . . , n x\preceq_{\mathcal{R}_+^n}y\iff x_i\le y_i,\ \ i=1,...,n x⪯R+ny⟺xi≤yi, i=1,...,n
- 矩阵不等式( K = S + n K=\mathcal{S}_+^n K=S+n)
X ⪯ S + n Y ⟺ Y − X 是半正定的 X\preceq_{S_+^n}Y\iff Y-X \text{是半正定的} X⪯S+nY⟺Y−X是半正定的
这两种类型很常见,所以有时会扔掉下标 K K K
性质: ⪯ K \preceq_K ⪯K 的性质很多和 R \mathcal{R} R 上 ≤ \le ≤ 的性质类似,比如:
x ⪯ K y , u ⪯ K v ⟹ x + u ⪯ K y + v x\preceq_K y,u\preceq_K v\implies x+u\preceq_K y+v x⪯Ky,u⪯Kv⟹x+u⪯Ky+v
Minimum and minimal elements
⪯ K \preceq_K ⪯K 并不是一个全序的(linear/total ordering),可以有 x ⋠ K y x\npreceq_Ky x⋠Ky 并且 y ⋠ K x y\npreceq_Kx y⋠Kx,也就是说这两个元素是不可比较的(incomparable)
比如说在 K = R + 2 K=\mathcal{R}_+^2 K=R+2 上:
[ 2 1 ] ⋠ [ 1 2 ] 并且 [ 2 1 ] ⋡ [ 1 2 ] \begin{bmatrix} 2\\ 1 \end{bmatrix} \npreceq \begin{bmatrix} 1\\ 2 \end{bmatrix} \text{并且} \begin{bmatrix} 2\\ 1 \end{bmatrix} \nsucceq \begin{bmatrix} 1\\ 2 \end{bmatrix} [21]⋠[12]并且[21]⋡[12]
也就是说这两个向量是不可比较的。
由此引出了很有趣的概念,在此意义下,最小值有两个概念:
x ∈ S x\in S x∈S 在 ⪯ K \preceq_K ⪯K 上是 the minimum element 时,
y ∈ S ⟹ x ⪯ K y y\in S\implies x\preceq_K y y∈S⟹x⪯Ky
x ∈ S x\in S x∈S 在 ⪯ K \preceq_K ⪯K 上是 a minimal element 时,
y ∈ S , y ⪯ K x ⟹ y = x y\in S,y\preceq_K x\implies y=x y∈S,y⪯Kx⟹y=x
比如 K = R + 2 K=\mathcal{R}_+^2 K=R+2 ,

minimum 是唯一的,并且有可能不存在,根据定义 S 1 S_1 S1 中任何一个点都要和 x 1 x_1 x1 能够比较,并且 x 1 x_1 x1 要小于等于他们,此时 x 1 x_1 x1 为 the minimum
minimal 是不唯一的,意思是假如说 S 2 S_2 S2 中存在点 y y y 是可以和 x 2 x_2 x2 相比较,并且 y y y 小于 x 2 x_2 x2,那么 y y y 一定等于 x 2 x_2 x2,此时 x 2 x_2 x2 是一个 minimal element,,图中 S 2 S_2 S2 左下角边上所有的点都是 minimal element
两种类型的判断方法:
- minimum:过该点画一个锥 K K K,保证集合 S S S 中的点全在锥中
- minimal:过该点画一个反向锥,保证集合 S S S 中只有一个点(也就是该点)在这个反向锥中