反向传播算法基于多元函数链式法则,以下记录多元函数链式法则的证明与反向传播算法的实例推演。
多元复合函数的求导法则(多元链式法则)
定义
如果函数$u=\varphi(t)$及$v=\psi(t)$都在点$t$可导,函数$z = f(u,v)$在对应点$(u,v)$具有连续偏导数(重点),那么复合函数$z = f[\varphi(t),\psi(t)]$在点$t$可导,且有:
$\displaystyle \frac{\mathrm{d}z}{\mathrm{d}t} = \frac{\partial z}{\partial u}\frac{\mathrm{d}u}{\mathrm{d}t}+ \frac{\partial z}{\partial v}\frac{\mathrm{d}v}{\mathrm{d}t} $
证明
设$t$获得增量$\Delta t$,此时$u = \varphi(t),v = \psi(t)$的对应增量为$\Delta u,\Delta v$,由此,$z=f(u,v)$获得增量$\Delta z$。因为函数$z = f(u,v)$在点$(u,v)$有连续偏导数,于是全增量$\Delta z$可表示为(全微分的充分条件):
$\displaystyle\Delta z = \frac{\partial z}{\partial u}\Delta u+ \frac{\partial z}{\partial v}\Delta v+\varepsilon_1\Delta u+\varepsilon_2\Delta v$
这里有,当$\Delta u\to 0,\Delta v\to 0$时,有$\varepsilon_1\to0,\varepsilon_2\to 0$。
上式两边各除以$\Delta t$,得:
$\displaystyle\frac{\Delta z}{\Delta t} = \frac{\partial z}{\partial u}\frac{\Delta u}{\Delta t}+ \frac{\partial z}{\partial v}\frac{\Delta v}{\Delta t}+\varepsilon_1\frac{\Delta u}{\Delta t}+\varepsilon_2\frac{\Delta v}{\Delta t}$
于是,取极限$\Delta t\to0$,就有:
$\displaystyle \frac{\mathrm{d}z}{\mathrm{d}t} = \frac{\partial z}{\partial u}\frac{\mathrm{d}u}{\mathrm{d}t}+ \frac{\partial z}{\partial v}\frac{\mathrm{d}v}{\mathrm{d}t} $
得证。(主要功劳在于它有连续偏导数,于是有全微分,才能用来加)
而神经网络中的多元函数大多是仿射函数(Softmax不是,但是也符合可微条件),符合上述全微分的充分条件,所以可以使用反向传播来计算所有参数的梯度。
反向传播算法的实例推演
反向传播的过程与公式推导(点击链接)不难,主要就是运用上述的多元函数链式法则。
但是看完原理后,代码如何实现呢?有个疑问就是,第n层的一个参数$w$,要使用第n+1层所有相关导数的累加,假设需要累加$n$次;而第n+1层的相关导数,又要第n+2层的所有相关导数的相关导数的累加,假设累加$m$次。也就是说,对于第n层的这个参数的导数,仅通过两层就要计算$n\times m$次。如此嵌套下去,要进行的加和运算似乎是指数级上升,这样是肯定不行的。可以想到,某些中间结果需要暂存,以防上述重复计算。以下直接举一个具体的例子来说明。
实例推演
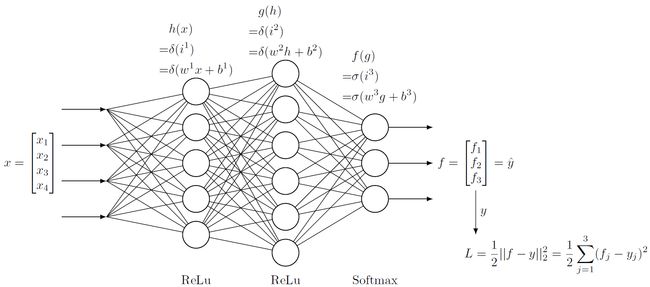
定义一个全连接网络,规模与各层激活函数如下图所示:
如图所示,神经网络使用MSE来作为损失函数。网络使用随机梯度下降,即每次传入一个样本。实际上,使用MSE时,批量梯度下降每次更新的梯度是批次中各个样本点梯度的简单相加,与随机梯度下降相比并没有其他复杂操作,所以这里只举随机梯度下降的为例。
每一层的操作都已在图中标出。其中$x\in R^4,y\in R^3$分别是样本的特征向量和标记向量;$h\in R^5,g\in R^6,f\in R^3$分别是输入层、隐层、输出层的输出向量;$w^k,b^k$分别是第$k$层用于仿射变换的矩阵和偏置向量,$i^k$是仿射变换的结果;$\delta(x)$是ReLu激活函数(对向量元素进行的运算),$\sigma(x)$是Softmax激活函数(对向量进行的运算)。
为了便于理解各个步骤之间的联系,以下将一些步骤的结果命名为大写字母。
首先算损失$L$对$f$的梯度,存入$A$中:
$ \displaystyle A =\frac{\partial L}{\partial f} = \left[ \begin{matrix} \frac{\partial L}{\partial f_1}\\ \frac{\partial L}{\partial f_2}\\ \frac{\partial L}{\partial f_3}\\ \end{matrix} \right] = \left[ \begin{matrix} f_1 - y_1\\ f_2 - y_2\\ f_3 - y_3\\ \end{matrix} \right] = f-y $
再算$f$对$i^3$的导数,由于激活函数使用的是Softmax,每个$i_k$都参与了每个$f_j$的计算,所以是一个雅可比矩阵:
$\displaystyle \begin{aligned} B &= \frac{\partial f}{\partial i^3}= \left[ \begin{matrix} \frac{\partial f_1}{\partial i^3_1}&\frac{\partial f_1}{\partial i^3_2}&\frac{\partial f_1}{\partial i^3_3}\\ \frac{\partial f_2}{\partial i^3_1}&\frac{\partial f_2}{\partial i^3_2}&\frac{\partial f_2}{\partial i^3_3}\\ \frac{\partial f_3}{\partial i^3_1}&\frac{\partial f_3}{\partial i^3_2}&\frac{\partial f_3}{\partial i^3_3}\\ \end{matrix} \right]= \left[ \begin{matrix} \frac{\partial \sigma_1(i^3)}{\partial i^3_1}&\frac{\partial \sigma_1(i^3)}{\partial i^3_2}&\frac{\partial \sigma_1(i^3)}{\partial i^3_3}\\ \frac{\partial \sigma_2(i^3)}{\partial i^3_1}&\frac{\partial \sigma_2(i^3)}{\partial i^3_2}&\frac{\partial \sigma_2(i^3)}{\partial i^3_3}\\ \frac{\partial \sigma_3(i^3)}{\partial i^3_1}&\frac{\partial \sigma_3(i^3)}{\partial i^3_2}&\frac{\partial \sigma_3(i^3)}{\partial i^3_3}\\ \end{matrix} \right]\\& =\left[ \begin{matrix} f_1-f_1f_1&-f_1f_2&-f_1f_3\\ -f_1f_2&f_2-f_2f_2&-f_2f_3\\ -f_1f_3&-f_2f_3&f_3-f_3f_3\\ \end{matrix} \right] =\text{diag}(f)-ff^T \end{aligned} $
于是$L$对$i^3$求梯度就是($\cdot$表示矩阵乘法):
$\begin{gather} C =\frac{\partial L}{\partial i^3} = \left[ \begin{matrix} \frac{\partial L}{\partial i^3_1}\\ \frac{\partial L}{\partial i^3_2}\\ \frac{\partial L}{\partial i^3_3}\\ \end{matrix} \right] =\left[ \begin{matrix} \sum_{j=1}^3\frac{\partial L}{\partial f_j}\frac{\partial f_j}{\partial i^3_1}\\ \sum_{j=1}^3\frac{\partial L}{\partial f_j}\frac{\partial f_j}{\partial i^3_2}\\ \sum_{j=1}^3\frac{\partial L}{\partial f_j}\frac{\partial f_j}{\partial i^3_3}\\ \end{matrix} \right] =B^T\cdot A \label{}\end{gather}$
接下来就是求$L$对参数$w^3$的梯度,但是它们中间有个$i^3$隔着,所以要先求$i^3$对$w$的导数。$i^3$是向量,$w^3$是矩阵,如果一一对应求导就变成了一个三维的张量(不知道有没有雅可比张量的说法)。但是可以发现,每个$w^3_{jk}$($j$行$k$列)只参与$i^3_j$的计算,所以每个$w^3_{jk}$只需求其对应的$i^3_j$的导数即可,求出的是一个矩阵(这一步在代码中并不需要计算,只是为了容易理解):
$\begin{gather}\displaystyle \frac{\partial i^3}{\partial w^3} =\left[ \begin{matrix} \frac{\partial i_1^3}{\partial w_{11}^3}&\cdots&\frac{\partial i_1^3}{\partial w_{16}^3}\\ \frac{\partial i_2^3}{\partial w_{21}^3}&\cdots&\frac{\partial i_2^3}{\partial w_{26}^3}\\ \frac{\partial i_3^3}{\partial w_{31}^3}&\cdots&\frac{\partial i_3^3}{\partial w_{36}^3}\\ \end{matrix} \right] =\left[ \begin{matrix} g_1&\cdots &g_6\\ g_1&\cdots &g_6\\ g_1&\cdots &g_6\\ \end{matrix} \right] =\left[ \begin{matrix} g_1^T\\ g_1^T\\ g_1^T\\ \end{matrix} \right] \label{}\end{gather}$
于是$L$对$w^3$的梯度就是($\times$表示按元素进行的乘法):
$\begin{gather}\displaystyle \frac{\partial L}{\partial w^3} =\left[ \begin{matrix} \frac{\partial L}{\partial i_1^3}\frac{\partial i_1^3}{\partial w_{11}^3}&\cdots&\frac{\partial L}{\partial i_1^3}\frac{\partial i_1^3}{\partial w_{16}^3}\\ \frac{\partial L}{\partial i_2^3}\frac{\partial i_2^3}{\partial w_{21}^3}&\cdots&\frac{\partial L}{\partial i_2^3}\frac{\partial i_2^3}{\partial w_{26}^3}\\ \frac{\partial L}{\partial i_3^3}\frac{\partial i_3^3}{\partial w_{31}^3}&\cdots&\frac{\partial L}{\partial i_3^3}\frac{\partial i_3^3}{\partial w_{36}^3}\\ \end{matrix} \right] =\left[ CCCCCC \right] \times \left[ \begin{matrix} g^T\\ g^T\\ g^T\\ \end{matrix} \right] =C\cdot g^T \label{}\end{gather}$
接下来求$L$关于$b^3$的导数,因为$b^3_k$的只参与$i^3_k$的计算,且导数为1,所以很简单:
$\begin{gather} \displaystyle \frac{\partial L}{\partial b^3} =\left[ \begin{matrix} \frac{\partial L}{\partial i^3_1}\frac{\partial i^3_1}{\partial b^3_1}\\ \frac{\partial L}{\partial i^3_2}\frac{\partial i^3_2}{\partial b^3_2}\\ \frac{\partial L}{\partial i^3_3}\frac{\partial i^3_3}{\partial b^3_3}\\ \end{matrix} \right] =\frac{\partial L}{\partial i^3}=C \label{}\end{gather}$
然后就要向前传播到隐层了,要算出$L$对$g$的梯度,首先要算出$i^3$对$g$的导数(这一步在代码中并不需要计算,只是为了容易理解):
$\begin{gather} \displaystyle \frac{\partial i^3}{\partial g} =\left[ \begin{matrix} \frac{\partial i_1^3}{\partial g_1}&\cdots&\frac{\partial i_1^3}{\partial g_6}\\ \frac{\partial i_2^3}{\partial g_1}&\cdots&\frac{\partial i_2^3}{\partial g_6}\\ \frac{\partial i_3^3}{\partial g_1}&\cdots&\frac{\partial i_3^3}{\partial g_6}\\ \end{matrix} \right] =w^3 \label{}\end{gather}$
分析可以发现,每个$g_j$都参与了所有$i^3_k$的计算,所以$L$对$g_j$的导数由多元函数链式法则可得:
$\displaystyle D =\frac{\partial L}{\partial g} =\left[ \begin{matrix} \frac{\partial L}{\partial g_1}\\ \vdots\\ \frac{\partial L}{\partial g_6}\\ \end{matrix} \right] =\left[ \begin{matrix} \frac{\partial L}{\partial i_1^3}\frac{\partial i_1^3}{\partial g_1} +\frac{\partial L}{\partial i_2^3}\frac{\partial i_2^3}{\partial g_1} +\frac{\partial L}{\partial i_3^3}\frac{\partial i_3^3}{\partial g_1}\\ \vdots\\ \frac{\partial L}{\partial i_1^3}\frac{\partial i_1^3}{\partial g_6} +\frac{\partial L}{\partial i_2^3}\frac{\partial i_2^3}{\partial g_6} +\frac{\partial L}{\partial i_3^3}\frac{\partial i_3^3}{\partial g_6}\\ \end{matrix} \right] ={w^3}^T\cdot C $
求出$L$对$g$的梯度后,就开始隐层各个参数的计算了。还是要一步一步算,首先算$g$关于$i^2$的梯度。因为隐层的激活函数是ReLu,是按元素进行的运算,所以每个$g_k$只对它对应的那个$i^2_k$求导。导数也很简单,判断大小即可:
$\displaystyle E =\frac{\partial g}{\partial i^2} =\left[ \begin{matrix} \frac{\partial g_1}{\partial i_1^2}\\ \vdots\\ \frac{\partial g_6}{\partial i_6^2}\\ \end{matrix} \right] =\left[ \begin{matrix} \delta'(i_1^2)\\ \vdots\\ \delta'(i_6^2)\\ \end{matrix} \right] ,\;\;\; \delta'(x) = \left\{ \begin{matrix} 1,x\ge0\\ 0,x<0 \end{matrix} \right. $
再求$L$关于$i^2$的梯度,它和$L$关于$i^3$的梯度$(1)$式不同,因为激活函数的计算方式不同:
$\displaystyle F =\frac{\partial L}{\partial i^2} =\left[ \begin{matrix} \frac{\partial L}{\partial i_1^2}\\ \vdots\\ \frac{\partial L}{\partial i_6^2}\\ \end{matrix} \right] =\left[ \begin{matrix} \frac{\partial L}{\partial g_1}\frac{\partial g_1}{\partial i_1^2}\\ \vdots\\ \frac{\partial L}{\partial g_6}\frac{\partial g_6}{\partial i_6^2}\\ \end{matrix} \right] = E\times D $
为了容易理解,在求$L$对$w^2$的梯度之前,先求$i^2$对$w^2$的导数,与$(2)$式类似,求出的是6行5列的矩阵:
$\displaystyle \frac{\partial i^2}{\partial w^2} =\left[ \begin{matrix} \frac{\partial i_1^2}{\partial w_{11}^2}&\cdots&\frac{\partial i_1^2}{\partial w_{15}^2}\\ \vdots&\vdots&\vdots\\ \frac{\partial i_6^2}{\partial w_{61}^2}&\cdots&\frac{\partial i_6^2}{\partial w_{65}^2}\\ \end{matrix} \right] =\left[ \begin{matrix} h_1&\cdots&h_5\\ &\vdots&\\ h_1&\cdots&h_5\\ \end{matrix} \right] =\left.\left[ \begin{matrix} h^T\\ \vdots\\ h^T\\ \end{matrix} \right]\right\} 6 \;r $
与$(3)$式类似,$L$对$w^2$的梯度就是:
$\displaystyle \frac{\partial L}{\partial w^2} =\left[ \begin{matrix} \frac{\partial L}{\partial i_1^2}\frac{\partial i_1^2}{\partial w_{11}^2}&\cdots&\frac{\partial L}{\partial i_1^2}\frac{\partial i_1^2}{\partial w_{15}^2}\\ \vdots&\vdots&\vdots\\ \frac{\partial L}{\partial i_6^2}\frac{\partial i_6^2}{\partial w_{61}^2}&\cdots&\frac{\partial L}{\partial i_6^2}\frac{\partial i_6^2}{\partial w_{65}^2}\\ \end{matrix} \right] = \left[FFFFF\right]\times \left.\left[ \begin{matrix} h^T\\ \vdots\\ h^T\\ \end{matrix} \right]\right\}6 \;r =F\cdot h^T $
与$(4)$式类似,$L$对$b^2$的梯度为:
$\displaystyle \frac{\partial L}{\partial b^2}= \frac{\partial L}{\partial i^2}=F $
现在,输出层与隐层的参数梯度已经计算完毕了。还剩输入层,它与隐层的唯一区别就在于层中元素数量不同,而传播与求梯度的方法和隐层是一样的,只需对输入层进行$(5)$式及以后的相应操作即可。
总结
通过以上的推演,可以发现,在全连接神经网络中,梯度$\frac{\partial L}{\partial i^k}$是关键。它涉及到参数$w^k$与$b^k$梯度的直接计算,是反向传播的载体。上面使用大写字母标记的变量中,实际上只有$\frac{\partial L}{\partial i^k}$多次参与计算。因此,在以上推演的反向传播中,真正要在迭代中暂存的只有$C$和$F$,其他步骤都合并在一个式子中完成即可。以下是迭代的示意图: