莱鸟学spss数据分析之第六章---描述性分析

第6章 描述性分析

数据的分布特征主要有三个：数据分布的集中趋势、数据分布的离散趋势、数据频数的分布形态。

6.1.1 集中趋势

集中趋势的目的是找到最能代表整个数据的数值。
1．适用类型
● 若为定类变量→计算众数。
●若为定序变量→计算众数或中位数。
●若为定距及定比变量→以下5种指标都可以。

2．描述数据集中趋势的5种指标
（1）众数
众数指一组数据中出现次数最多的数值。例如在一组数据10、12、18、24、12、20、12、15、10、23、18中，众数为12。

（2）中位数

中位数指将数据按大小顺序排列，排在中间位置的数值。例如在一组数据10、12、15、18、23中，中位数为15；在10、12、13、15、18、23这组数据中，中位数为14（(13+15)/2），由此可知，中位数不一定存在于原始数据中。

注意：当有极端值、偏态分布、数据分布不对称时，使用中位数，但中位数无法反映所有样本的情况。

（3）算术平均数
算术平均数指一组数据的平衡点。若一组数据中没有极端值，则平均数考虑了所有的信息量，是最有代表性的数值；平均数易受极端值的影响，若存在极端值，则最好用截尾均数或中位数来代替平均数。
（4）截尾均数
平均数易受极端值的影响，可以通过截去极端数据（具体去掉多少根据实际情况而定），只求去掉极端值后剩下数值的均数，在SPSS的“探索性分析”中可以自动计算“5%剪除后平均值”。

（5）加权平均数
加权平均数指当一组数据中各个数据的重要性不一样或者各组数据的样本数量不同时，需要给每个数据赋予不同的权重来权衡轻重，以此赋予每个数据同样的重要性，再做平均数的计算。例如，在公务员考试中包含笔试和面试，满分都为100分，其中笔试占70%、面试占30%，那么最终的成绩为：(笔试分数×70%+面试分数×30%)/2。

6.1.2 离散趋势

离散趋势可以说明集中趋势指标的代表性如何，也用来在统计推断时计算误差的大小，离散程度越大，变异程度越大。
1．适用类型
●若为定类变量→计算全距。
● 若为定序变量→计算全距、四分位数。
●若为定距及定比变量→以下5种指标都可以。
2．描述数据离散趋势的5种指标
（1）全距
全距又称极差，在SPSS 24中称为“范围”，是一组数据中最大值与最小值的差。通过全距可以粗略地了解数据的分布范围。在同类离散指标比较时，全距越大，数据的离散程度越大；全距越小，数据的离散程度越小。在日常生活中温差就是一种全距，在实际工作中全距常用来检查产品质量是否稳定，以此对质量进行控制。

（2）四分位数
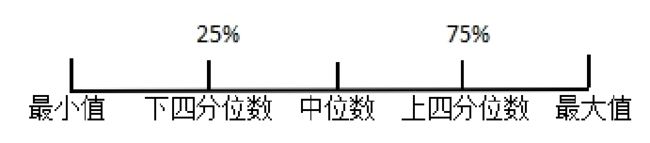
将数据从小到大排序，分成四等份，每份各占25%，上四分位数为75%处的值，下四分位数为25%处的值，如图6.1.2所示，数值越大，个体差异度越大。

​

使用四分位数还可以判断变量分布是否对称。四分位差=1/2(上四分位数-下四分位数)。
（3）方差与标准差
方差与标准差属于绝对差异量，主要用来衡量观测值与平均值间的离散程度。方差与标准差也容易受极端值的影响。
●标准差是方差的平方根，考虑了数据分布的疏密程度，标准差越大，表明各数值不在均值的附近。变量值之间的差异越大，数据分布的离散程度越大；差异越小，数据分布的离散程度越小。
● 只有当标准差差异不大时，比较多组数据的均值才有意义。
●方差可以进行进一步计算，而标准差不能进行进一步计算，所以在推论统计中通常使用方差。
●方差、标准差只适用于正态分布资料。

（4）变异系数
变异系数属于相对差异量。若两组数据的性质、单位等不同，无法用方差和标准差来比较其离散程度，此时就需要用变异系数。例如，要比较身高和体重的离散程度，由于身高和体重的单位不同，所以需要用变异系数。变异系数=标准差/平均值。
3．集中趋势与离散趋势的匹配

在对一组数据进行分析时，通常会将集中趋势与离散趋势结合起来描述数据特征，此时就需要注意二者的匹配。若集中趋势的指标为平均数，则离散趋势的指标要为方差或标准差；若集中趋势的指标为中位数，则离散趋势的指标要为全距、四分位差；若数据有极端值，则最好用中位数、上四分位数和下四分位数、最大值、最小值来描述。

6.1.3 分布形态

1．正态分布
正态分布曲线为一条对称的曲线，标准差越大，曲线越矮阔，个体差异越大，如图6.1.3所示。

​
标准正态分布的均值为0，标准差为1。在SPSS中，任何数据都可以变换为标准正态分布，只需要在“描述性分析”中勾选“将标准化值另存为变量”选项即可。

2．偏度
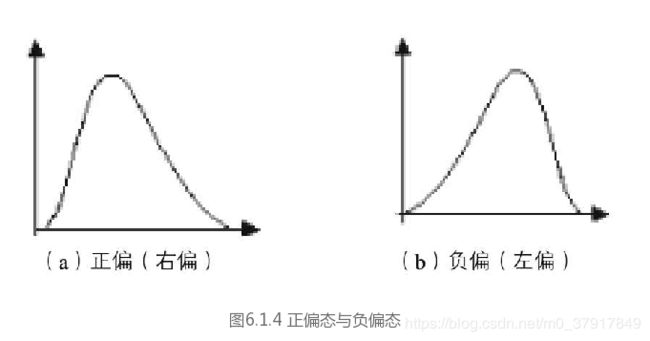
偏度指统计数据分布不对称的方向和程度。偏度>0为正偏态，长长的尾巴在右侧；偏度<0为负偏态，长长的尾巴在左侧，如图6.1.4所示。一般来说，当总频数大于200时，偏度才算可靠。

​

（1）正偏态

若为正偏态，则众数<中位数<平均数，如图6.1.5所示。
（2）负偏态
若为负偏态，则中位数<平均数<众数，如图6.1.6所示。

​

3．峰度

峰度指分布图形的峰凸程度。峰度>0为尖峰分布，尖峰分布比正态分布更陡峭，峰形较尖；峰度＜0为低峰分布，低峰分布比正态分布更矮阔，峰形较短胖，如图6.1.7所示。一般来说，当总频数大于1000时，峰度才算可靠。

6.2 频率分析

频率分析是数据分析最常用的方法之一，主要利用统计量和图表来反映数据的分布特征，比如频数分布表、条形图、直方图、集中趋势和离散趋势的各种统计量（平均值、中位数、偏度和峰度等），我们可以通过频率分析对要分析的数据进行初步的了解和判断。需要注意的是，分类变量和连续变量的频率分析是不同的，我们将分别进行具体的讲解。

6.2.1 分类变量的频率分析

6.2.2 连续变量的频率分析

统计表让我们了解到数据的集中趋势和离散趋势，直方图使我们清晰地判断出“年龄”这个变量大致服从正态分布。

6.3 描述统计

6.3.1 描述统计概述

在进行数据分析之前，一般要对数据进行描述工作，描述统计量包括均值、方差、标准差、全距等，还可以将原始分数转换为Z分数，生成Z分数的新变量。通过这些描述统计量，我们会对数据有一个具体的了解。

6.4 探索性分析

探索性分析是在一般描述统计指标的基础上增加了关于数据其他特征的文字与图形描述，是对描述统计分析更加深入和详尽的分析，使分析结果更加细致与全面。本节将以数据文件“身高体重.sav”为例剖析探索性分析。

探索性分析可以生成关于所有个案或不同分组个案的综合统计量及图表，也可以对数据进行筛选，例如检测异常值、极端值等。通过探索性分析，我们能决定选择何种统计方法进行数据建模，判断是否需要把数据转换成正态分布等。