古典密码加密与解密
移位密码
加密:
明文 x x x,密文 y ( x ) y(x) y(x)
y ( x ) = ( x + K ) m o d 26 y(x) = (x + K)mod\ 26 y(x)=(x+K)mod 26
解密:
密钥穷尽搜素法:从1开始进行尝试,知道找到有意义的明文和密钥K。
代换密码
对字母进行一定形式的代换,共有 26 ! 26! 26!种代换方式如下,小写字母表示明文,大写字母表示密文:

可见,移位密码是代换密码的一种特殊形式。
加密:
e π ( a ) = X , e π ( b ) = N , … e_{\pi}(a) = X,e_{\pi}(b) = N,\dots eπ(a)=X,eπ(b)=N,…
解密:
根据26个字母在自然条件下的使用频率来进行推演,同时合理利用双字母组合sh、gh、th等的使用频率来进行分析。
26个字母的自然概率统计表如下:

仿射密码
是代换密码的另一种特殊形式,在移位密码的基础上更进一步。
加密:
要求 g c d ( a , 26 ) = 1 gcd(a, 26) =1 gcd(a,26)=1。
e ( x ) = ( a x + b ) m o d 26 e(x) = (ax + b) mod\ 26 e(x)=(ax+b)mod 26
当 a = 1 a=1 a=1时,即为移位密码。
解密:
令 y ≡ a x + b ( m o d 26 ) y\equiv ax+b\ (mod\ 26) y≡ax+b (mod 26),反解该同余式有 a x ≡ y − b ( m o d 26 ) ax\equiv y-b\ (mod\ 26) ax≡y−b (mod 26),若 x x x有且仅有唯一解,则 g c d ( a , 26 ) = 1 gcd(a,26)=1 gcd(a,26)=1。
x ≡ a − 1 ( y − b ) ( m o d 26 ) x\equiv a^{-1}(y-b)\ (mod\ 26) x≡a−1(y−b) (mod 26)
维吉尼亚密码
一种多表代换密码。
加密:
每m个明文为一组,分组进行多表加密。
密钥 K = ( k 1 , k 2 , … , k m ) K=(k_1, k_2, \dots , k_m) K=(k1,k2,…,km)
e K ( x 1 , x 2 , … , x m ) = ( x 1 + k 1 , x 2 + k 2 , … , x m + k m ) e_K(x_1, x_2, \dots , x_m)=(x_1+k_1, x_2+k_2, \dots , x_m+k_m) eK(x1,x2,…,xm)=(x1+k1,x2+k2,…,xm+km)
解密:
第一步:确定分组大小 m m m。
Kasiski测试法:搜索长度至少为3的相同的密文段,记下其与起始点密文段的距离 δ \delta δ,对得到的 δ 1 , δ 2 , … , δ n \delta_1, \delta_2, \dots , \delta_n δ1,δ2,…,δn求最大公因数,则m很可能为该最大公因数。
重合指数法:反映字母分布。猜测出m后,可用重合指数法进行再次判断,验证该m的可信度。
因此,由于对于分组长度为m进行加密的字符串,每隔m位使用的是相同的移位数,因此,其字母分布应接近自然条件下的字母分布,即重合指数应接近0.065;对于间隔非m的字符,由于加密时使用的不是相同的位移数,因此,不符合自然条件下字母分布情况,即重合指数很不接近0.065。
故,可将密文串进行分组,逐个计算重合指数,如下:

第二步:通过穷尽密钥搜索来确定每个位置的移位大小。
希尔密码
另一种多表代换密码。
加密:
要求矩阵K必须为可逆矩阵。
密钥 K K K为 m × m m\times m m×m的矩阵
( y 1 , y 2 , … , y m ) = ( x 1 , x 2 , … , x m ) ( k 1 , 1 k 1 , 2 … k 1 , m k 2 , 1 k 2 , 2 … k 2 , m ⋮ ⋮ ⋱ ⋮ k m , 1 k m , 2 … k m , m ) (y_1, y_2, \dots ,\ y_m)=(x_1, x_2, \dots ,\ x_m)\begin{pmatrix} k_{1,1}&k_{1,2}&\dots &k_{1,m}\\ k_{2,1} &k_{2,2}&\dots &k_{2,m}\\ \vdots &\vdots &\ddots &\vdots\\ k_{m,1} &k_{m,2} &\dots &k_{m,m}\end{pmatrix} (y1,y2,…, ym)=(x1,x2,…, xm)⎝⎜⎜⎜⎛k1,1k2,1⋮km,1k1,2k2,2⋮km,2……⋱…k1,mk2,m⋮km,m⎠⎟⎟⎟⎞
即 y = x K y=xK y=xK
解密:
x = y K − 1 x=yK^{-1} x=yK−1
该解密过程的前提为,密钥K必须为可逆矩阵,对于字母来说,要求改可逆矩阵满足 g c d ( ∣ K ∣ , 26 ) = 1 gcd(|K|,26)=1 gcd(∣K∣,26)=1。
例题:
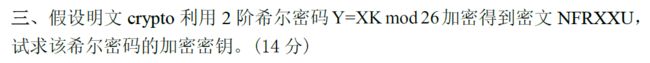
K = X − 1 Y K = X^{-1}Y K=X−1Y
明文:crypto = (2, 17, 24, 15, 19, 14)
密文:NFRXXU = (13, 5, 17, 23, 23, 20)
取前四组数据,有 X = ( 2 17 24 15 ) X=\begin{pmatrix} 2&17\\ 24 &15\end{pmatrix} X=(2241715),则 ∣ X ∣ = ( 2 ∗ 15 − 17 ∗ 24 ) m o d 26 = 12 |X| = (2*15-17*24)mod\ 26=12 ∣X∣=(2∗15−17∗24)mod 26=12,由于 g c d ( 12 , 26 ) = 2 ≠ 1 gcd(12,26)=2\not=1 gcd(12,26)=2=1,因此该X不能反求出K。
取 X = ( 2 17 19 14 ) X=\begin{pmatrix} 2&17\\ 19 &14\end{pmatrix} X=(2191714),则 ∣ X ∣ = ( 2 ∗ 14 − 17 ∗ 19 ) m o d 26 = 17 |X| = (2*14-17*19)mod\ 26=17 ∣X∣=(2∗14−17∗19)mod 26=17,由于 g c d ( 17 , 26 ) = 1 gcd(17,26)=1 gcd(17,26)=1,因此该X成立,可反求出: K = ( 2 17 19 14 ) − 1 ( 13 5 23 20 ) = 1 7 − 1 × ( 14 9 7 2 ) ( 13 5 23 20 ) = 23 × ( 14 9 7 2 ) ( 13 5 23 20 ) = ( 3 4 5 9 ) \begin{aligned}K&=\begin{pmatrix} 2&17\\ 19 &14\end{pmatrix}^{-1}\begin{pmatrix} 13 &5\\ 23 &20\end{pmatrix}\\ &=17^{-1}\times\begin{pmatrix} 14&9\\ 7 &2\end{pmatrix}\begin{pmatrix} 13 &5\\ 23 &20\end{pmatrix}\\ &= 23\times \begin{pmatrix} 14&9\\ 7 &2\end{pmatrix}\begin{pmatrix} 13 &5\\ 23 &20\end{pmatrix}\\ &= \begin{pmatrix} 3&4\\ 5 &9\end{pmatrix} \end{aligned} K=(2191714)−1(1323520)=17−1×(14792)(1323520)=23×(14792)(1323520)=(3549)
注意:伴随矩阵要进行转置!!!
置换密码
保持明文字母不变,只打乱明文顺序。
其置换函数是一个双射函数,置换密码是希尔密码的一种特殊形式。
加密:
e π ( x 1 , x 2 , … , x m ) = ( x π ( 1 ) , x π ( 2 ) , … , x π ( m ) ) e_{\pi}(x_1,x_2,\dots,x_m)=(x_{\pi(1)},x_{\pi(2)},\dots,x_{\pi(m)}) eπ(x1,x2,…,xm)=(xπ(1),xπ(2),…,xπ(m))
举例:
将原来第3个字母放至第一个;将原来第5个放至第2个,……
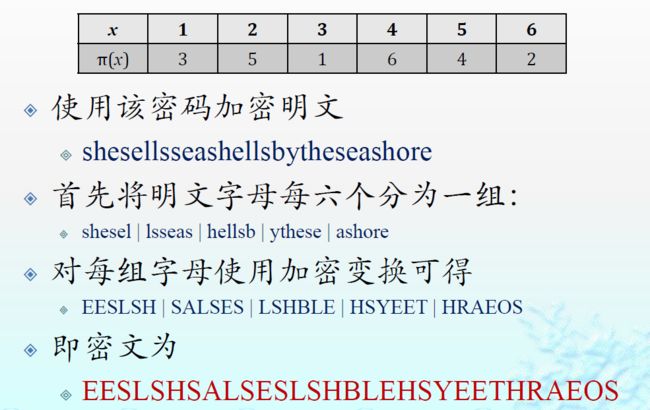
解密:
d π ( y 1 , y 2 , … , y m ) = ( y π − 1 ( 1 ) , y π − 1 ( 2 ) , … , y π − 1 ( m ) ) d_{\pi}(y_1,y_2,\dots,y_m)=(y_{\pi^{-1}(1)},y_{\pi^{-1}(2)},\dots,y_{\pi^{-1}(m)}) dπ(y1,y2,…,ym)=(yπ−1(1),yπ−1(2),…,yπ−1(m))
举例:
将原来第3个字母放至第1个;将原来第6个放至第2个,……

例题:

该题由于不存在不同位置字母移位不同的问题,因此不需要分类进行重合指数的计算,直接对全部字符串计算重合指数即可。
流密码
加密:
密钥流 z = z 1 z 2 … z=z_1z_2\dots z=z1z2…
y = y 1 y 2 ⋯ = e z 1 ( x 1 ) e z 2 ( x 2 ) … y=y_1y_2\dots=e_{z_1}(x_1)e_{z_2}(x_2)\dots y=y1y2⋯=ez1(x1)ez2(x2)…
常利用线性反馈移位寄存器LFSR来产生自动密钥流,下一位密钥由前几个密钥中的几个决定。
解密:
第一步:通过已知的明文和部分密文流计算出密钥流,对名密文进行异或操作即可得到密钥流;
- 明文:1 0 1 1 0 1 0 1 1 1 1 0 0 1 0
- 密文:0 1 1 0 0 1 1 1 1 1 1 1 0 0 0
- 密钥:1 1 0 1 0 0 1 0 0 0 0 1 0 1 0
第二步:若已知密钥为m级,可通过密钥流解出对应的密钥流产生递推公式;
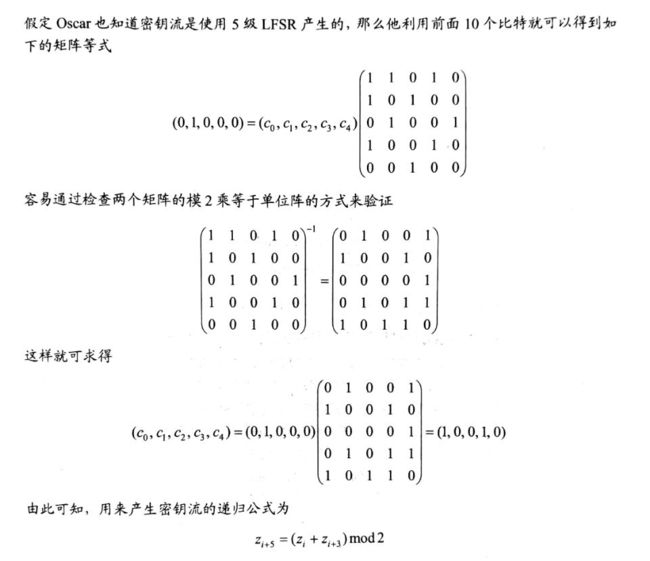
第三步:根据明文和密钥流递推公式计算密文。





