第一个用python实现的数据化运营分析实例——销售预测
案例场景:每个销售型公司都有一定的促销费用,促销费用可以带来销售量的显著提升;当给出一定的促销费时,预计会带来多大的商品销售量?
原始数据:data.txt 文件 ,包含了建模所需的原始数据
依赖库:re、numpy、sklearn、matplotlib
纬度数量:1
记录数:100
x:促销费用 y:商品销售量
python IDE:PyCharm
python版本:Python 3.7.2
案例过程:
第一步:导入库
import re
import numpy
from sklearn import linear_model
from matplotlib import pyplot as plt导入库:import [库名]
导入库中指定函数:from [库名] import [函数名]
第二步:导入数据
fn = open('data.txt','r')
all_data = fn.readlines()
fn.close()读取文件,并保存至变量all_data中,注意open参数的文件名可以是绝对路径,也可相对路径。
第三步:数据预处理
x = []
y = []
for single_data in all_data:
tmp_data = re.split('\t|\n',single_data)
x.append(float(tmp_data[0])
y.append(float(tmp_data[1])
x = numpy.array(x).reshape([100,1])
y = numpy.array(y).reshape([100,1])用正则分割每行数据,赋值给x和y,将x:促销费用 y:商品销售量 的列表转换成x和y数组类型。
第四步:数据分析
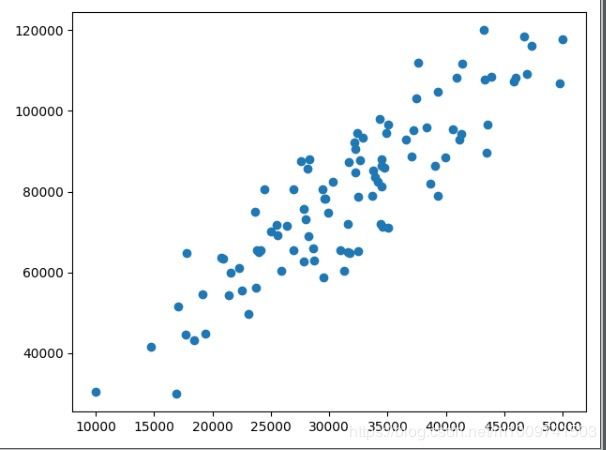
pltscatter(x,y)
plt.show()plt.scatter(x,y) 用一个散点图来展示x和y。plt.show() 是展示图像(二维图像),
该图像为线性回归模型处理更为准确。
第五步:数据建模
model = linear_model.LinearRegression()
model.fit(x,y)先创建一个模型对象,后续所有的模型操作都基于该对象上产生。然后model.fit(x,y) 将x和y分别作为自变量和因变量输入模型进行训练。
第六步:模型评估
model_coef = model.coef_
model_intercept = model.intercept_
re = mode.score(x,y)
model_coef = model.coef_ :获取模型的自变量的系数并赋值为model_coef;
model_intercept = model.intercept_ :获取模型的截距并赋值为model_intercept;
re = mode.score(x,y) : 获取模型的决定系数R的平方。
上述步骤可得到线性回归方程 y = model_coef*x + model_intercept ,即 y = 2.09463661*x + 13175.36904119 。该方程决定系数R的平方是0.78764146847589545 。
第七步:销售预测
new_x=[]
new_x.append(float("84610"))
new_x = numpy.array(new_x).reshape([-1, 1])
pre_y = model.predict(new_x)
print(pre_y)创建促销费用常量,作为预测的输入,pre_y = model.predict(new_x) 作用是对促销费用常量new_x输入模型进行预测,最后打印出来[[190402.57234225]]。注意perdict()的第一个参数需要为numpy数组类型。
至此,已完成功能需求代码编写与测试。