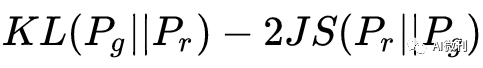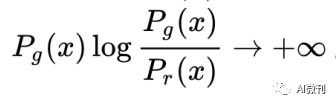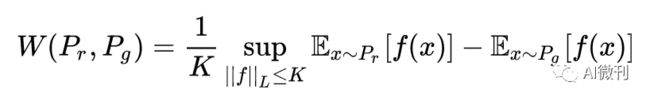GAN ZOO 第2节： 对原始GAN的损失函数进行改进：LSGAN、WGAN、WGAN-GP

“GAN ZOO”系列文章说明

    GAN成为当下研究热点，相关论文数量正在以指数趋势增长，如上图所示。

    为了便于大家迅速追踪研究热点，“AI微刊”团队持续推出“GAN ZOO”系列文章，精选典型GAN模型，对其进行精简的解析，让你“三分钟”读一篇论文。

 

GAN ZOO 第2节：

对原始GAN的损失函数进行改进：LSGAN、WGAN、WGAN-GP

PS：本文知识点高度密集，建议码起来，电脑端阅读。

本文是“GAN ZOO”系列第2节，将为您：

• 分析原始GAN损失函数带来梯度消失、模式崩溃等问题的原因；
• 介绍经典改进模型模型：LSGAN、WGAN、WGAN-GP。

 

---

4. 最小二乘GAN（LSGAN）：LSGAN用最小二乘损失函数替换交叉熵损失函数，加大对离群样本的惩罚

本论文首次发表于2016.11.13

 

4.1 原始GAN的缺陷

    原始GAN使用Sigmoid交叉熵损失函数，容易造成梯度消失问题，使得生成器G的训练不充分。

    具体阐述为：

    原始GAN的损失函数为Sigmoid交叉熵：

    如下图，蓝线是判别器D的真假样本决策边界，蓝线右下方的样本判为真，左上方判为假。由于判别器被欺骗，因此将一部分真样本（黄色圆圈o）判为假，将一部分假样本（蓝色十字+）判为真。

    对于被判为“真”，但是又远离真实样本分布的假样本（图中粉色五角星☆虽然被判为真，但是离黄色圆圈o较远），这些样本被判别器D打上了“真”的标签，即D(G(z))=1，因此在损失函数中表现为生成器G的损失函数值为0，如下所示：

    此时，G的损失函数的导数趋近于0，更新梯度趋近于0，出现梯度消失，G不能再得到训练。

    简单来说，有的生成样本虽然成功欺骗了判别器D，但是其依然与真实样本的分布相差较远。Sigmoid交叉熵只管真假、不管距离，不会再惩罚这种样本，导致生成器G出现梯度消失。

 

4.2 LSGAN的改进

4.2.1 LSGAN的思想

    Sigmoid交叉熵适合用于逻辑分类，而最小二乘损失函数适合线性回归。因此，为了迫使生成样本尽可能地拟合真实样本的分布，本论文采用最小二乘损失函数替代Sigmoid交叉熵，缓解梯度消失问题。

4.2.2 LSGAN的模型

（1）LSGAN的损失函数：

    在判别器D的输出层中去掉Sigmoid激活函数，并且在损失函数中去掉Log，使用最小二乘损失函数。使得D不仅判别真假，还惩罚离群的生成样本（实际上，离决策面越远的样本对生成器更新梯度的贡献越大），使生成样本不断向真实样本分布靠近。如下图所示：

4.2.3 LSGAN的缺点

    LSGAN对离群样本的惩罚机制要求所有的生成样本分布，导致样本生成的”多样性”降低, 生成的样本很可能只是对真实样本的简单”模仿”和细微改动。

 

4.3 LSGAN的实验

    作者将LSGAN用于手写汉字数据库（含3740个汉字），最终生成了可读的汉字，从图中可以看出。

 

参考

[1] “LSGAN：最小二乘生成对抗网络”，机器之心

https://www.jiqizhixin.com/articles/2018-10-10-11；

 

---

5. Wasserstein GAN（WGAN）：WGAN改善GAN的梯度消失问题、模式崩溃问题

本论文次发表于2017.1.26

 

5.1 原始GAN的缺陷

    原始GAN的损失函数存在缺陷：当D训练得越好，G的梯度消失越严重，限制了G的训练。

    具体阐述为：

    简单理解，原始GAN生成器损失函数为：

    该公式通过一定变换后，可以用JS散度表示为：

    根据以上公式可以推理出如下三点：

1. 生成器G的目标就是通过梯度下降法减小Pg与Pr之间的JS散度，使生成样本分布Pg逼近真实样本分布Pr。
2. 但是，如果Pg与Pr之间的重叠部分接近于0，那么其JS散度就是常数log2，其梯度为0，无法使用梯度下降法进行学习。
3. 并且，Pg与Pr之间的重叠部分为0的概率非常大【注解1】。此外，随着D判别Pg与Pr的能力增强，重叠部分将越来越小。

    因此，原始GAN的不稳定表现为：如果D训练得太好，G的loss趋近于常数，梯度为0，无法进行梯度下降；另一方面，如果D训练得不好，G的梯度不稳，难以向Pr收敛【注解2】。

 

    PS：在原始GAN后，WGAN前，Ian Goodfellow对G的损失函数进行了改进，改为：

    但这个-logD(x)函数却存“自相矛盾”与“惩罚偏好”两个问题【注解3】，导致GAN训练不稳定，并且容易出现模式崩溃。

 

【注解1】 Pg与Pr之间的重叠部分为0的概率较大

    原因是：生成器G将低维噪声Pz映射为高维样本Pg（比如从100维映射为784维），784维的Pg的各种变化已经被100维的Pz限定死了，也就是Pg实际上是在784维空间定义了一个100维的数据分布（学术层面上来讲就是，生成样本的分布Pg实际上是高维空间中的低维流形）。然而另一方面，Pr本身就是高维的，也就是在784维空间定义了一个784维的数据分布。类比到三维空间，Pg是二维的面或者一维的线，而Pr充满三维空间，Pg与Pr之间的重叠部分就只会是一个面或者一条线，在三维空间中相当于“0” （高维空间中的低维流形与高维流形之间的重叠几乎为“0”）。

       因此，如果D接近最优，判别能力较强，也就是能够完全将Pg与Pr分开，那么Pg与Pr之间的JS散度就接近常数，求导为0。

【注解2】如果D训练得不好，G的梯度不稳，难以向Pr收敛

    Pz从低维空间映射到高维空间的映射方式有无数种，映射结果又无数种可能性，如果D的判别能力较弱，G就可能不受约束，向着不满足要求的方向映射。

【注解3】-logD(x)函数的“自相矛盾”与“惩罚偏好”问题

    生成器损失函数为：

    该函数可以被变换为：

    根据该公式可以看出损失函数具有以下两个问题：

（1）自相矛盾：

       最小化改损失函数的时候就相当于最小化KL距离，同时最大化JS散度，自相矛盾。

（2）惩罚偏好：

    KL距离是非对称的，导致GAN对以下两种错误的惩罚力度不同：

    当Pg→0，Pr→1，即Pg的多样性远低于Pr，对 KL距离贡献为0，惩罚微小；

    当Pg→1，Pr→0，即Pg的多样性远高于Pr，对KL距离贡献为无穷，惩罚巨大；

    基于此， G更倾向于舍弃多样性，而生成“重复且安全”样本，带来模式崩溃问题。

 

5.2 WGAN的改进

5.2.1 WGAN的思想

    使用Wasserstein距离（Earth-Mover，EM距离【注解4】）替代原损失函数。

【注解4】Earth-Mover（推土机）距离

    函数中，E(||x-y||)可以理解为将Pr这堆“沙土”挪到Pg“位置”所需的能量，而W(Pg,Pr)就是在“最优路径”下最小的能量消耗。

    Wasserstein距离相比KL散度、JS散度的优越性在于，即便两个分布之间没有重叠，Wasserstein距离仍然能够反映它们的远近，因此有连续的梯度。

5.2.2 LSGAN的模型

（1）WGAN的损失函数：

    但是Wasserstein距离应用较难，需要进行变换，经过变换后WGAN的损失函数为（具体变换见论文原文）：

    该函数的意思就是要求搜索所有Lipschitz常数【注解5】小于K的函数f，并取f在后面那一坨的上确界，并除以K。

       由于函数f有很多中形式，因此选择用神经网络来拟合或者囊括尽可能多的f。

【注解5】Lipschitz常数

    连续函数f如果在其定义域内的导数f’的绝对值|f’|满足以下条件：

    就称这个函数是Lipschitz连续的，并且称K为Lipschitz常数。

（2）WGAN的算法流程：

（3）WGAN的改进之处：

    简单来说WGAN相对于GAN的改变就是一下四点：

• 判别器最后一层去掉Sigmoid；
• 生成器和判别器的loss不取log；
• 每次得到D的参数更新值之后，将其剪切（Chip）到一个较小的区间[-c,c]，使其满足Lipschitz条件；
• 不要用基于动量的优化算法（包括momentum和Adam），推荐RMSProp，SGD也行

 

参考

[1] “令人拍案叫绝的Wasserstein GAN”，知乎

https://zhuanlan.zhihu.com/p/25071913；

 

 

6. WGAN-GP：WGAN-GP改善WGAN梯度剪切问题

本文次发表于2017.12.25

 

6.1 原始WGAN的缺陷

    本文的三作Martin Ajorvsky是WGAN论文中的一作，本文是对WGAN的梯度剪切问题的改进。

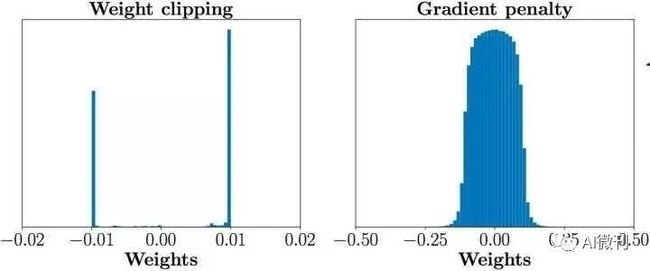
    原始WGAN为实现Lipschitz连续条件，将D的参数更新值剪切到较小的区间[-c,c]，这使得参数在-c与c两点处聚集，限制拟合能力，如图：

    下图是随着判别器层数增大，梯度范数的Log值的变化曲线，可见WGAN的三条曲线都出现了梯度消失或者梯度爆炸，WGAN-GP则比较平稳。

 

6.2 WGAN-GP的改进

6.2.1 WGAN-GP的思想

    直接剪切太过于武断，那就换一种柔和的方式。WGAN-GP将直接剪切替换为一个惩罚项，通过惩罚项限制梯度的值。

6.2.2 WGAN-GP的模型

（1）WGAN-GP的损失函数：

    WGAN-GP在原WGAN的损失函数后面添加了惩罚项：

    惩罚项中的1本来是Lipschitz常数K，目的是使得D的梯度既满足Lipschitz条件（导数梯度不超过K），同时也不会太小（太小则学习太慢）。论文中为了简便，将K定义为1。

注意事项：

• 随机采样：不需要对所有样本都执行惩罚项，只需要在真假样本最容易混淆的区域每次随机采样部分样本，对其执行惩罚，这样可以减小计算难度。
• 惩罚项因子：惩罚项因子λ需要调试，本论文中使用的都是λ=1。
• Batch Normalization：本文的梯度惩罚是对每个样本单独施加的，如果引入Batch Normalization会使得同个batch中不同样本出现相互依赖的情况，因此建议不使用Batch Normalization，或者使用不会产生样本依赖的Layer Normalization等。

 

（2）WGAN-GP的算法流程：

 

参考

[1] “WGAN-GP与WGAN及GAN的比较”，CSDN

https://blog.csdn.net/qq_38826019/article/details/80786061；

[2] “WGAN最新进展：从weight clipping到gradient penalty”，炼数成金

http://www.dataguru.cn/article-11229-1.html；

 

 

本文完

关注本公众号“AI微刊”，后台发送“GAN ZOO”，即可获得GAN ZOO系列论文包以及源代码资源包。

 

微信号：AI微刊

 

后台发送“GAN ZOO ”，即可获得GAN ZOO系列论文包以及源代码资源包。