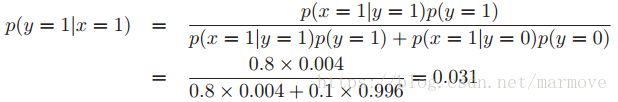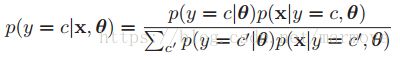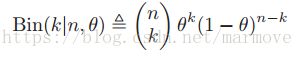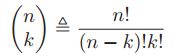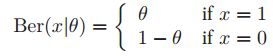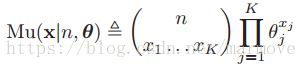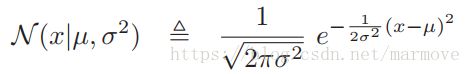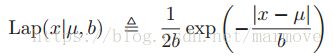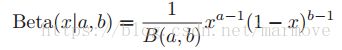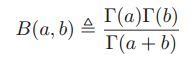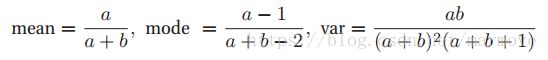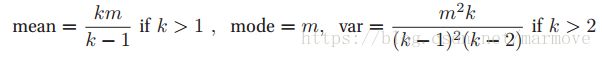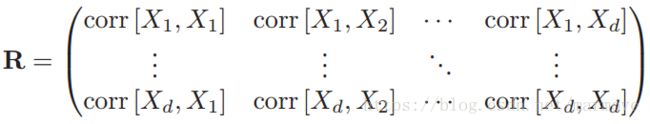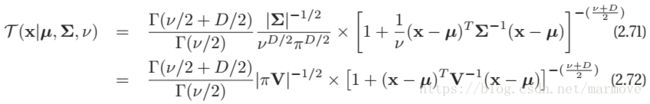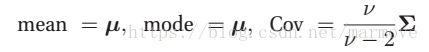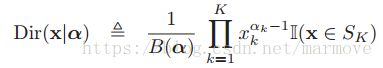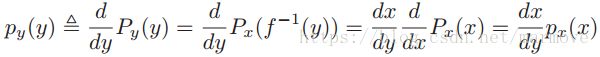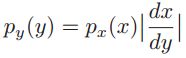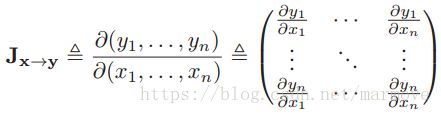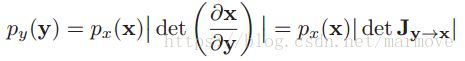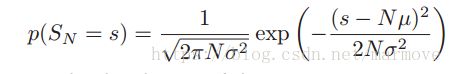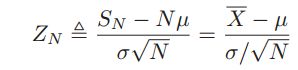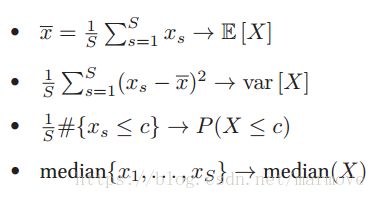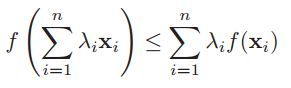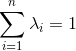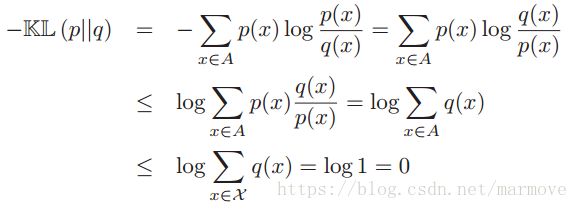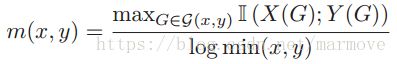MLAPP————第二章 概率论基础
说明
这篇博客主要是介绍概率论还有信息论的一些预备知识。主要以翻译为主,很多地方的结论也都是根据书上直接得到的,没有给出具体的求解过程。
第二章 概率
2.1 介绍
在进行更加技术性的内容之前,先不妨想一下什么是“概率”?我们经常会说:丢一枚硬币,正面朝上的概率是0.5。这句话的意思是什么。有两种不同的观点,一个是频率派的观点,他们认为概率就是你重复做一件事N次,如果事件发生了m次,那么概率就是m/N。从抛硬币角度,就是你抛了特别多次,那么往往有一半是正的,一半是反的。另一个则是贝叶斯(Bayesian)派的观点。他们是基于一些信息去量化某件事的不确定性。比如我认为硬币是密度均匀的,对称的圆的形状,所以我认为它正反的概率都是一样的0.5。贝叶斯解释的最大的好处就是它不需要多次重复尝试,比如问你地球什么时候毁灭,南极什么时候融化,这些问题都只能基于你拥有的信息,去给出这个事件发生的可能性。因为这种事件是不可重复的。
2.2 概率论的简要温习
这一部分内容主要就是对概率论的一些基本的内容进行简要的回顾。
2.2.1 离散随机变量
这里不具体详述,举个简单的例子,还是投一枚硬币,对于这个事件A,发生的情况有两种正面朝上,反面朝上。那么离散随机变量X的取值为0或者1。其概率分布就叫做pmf(probability mass function)。![]() ,
,![]() 。
。
2.2.2 基本的运算法则
2.2.2.1 两个事件的并集的概率
![]() ,如果A和B是互斥的,那么
,如果A和B是互斥的,那么![]() 。
。
2.2.2.2 联合概率
A和B的联合概率![]() ,这个也叫乘法原理。对于一个联合概率分布,我们可以计算它的边缘概率分布p(A),
,这个也叫乘法原理。对于一个联合概率分布,我们可以计算它的边缘概率分布p(A),![]() ,这个也叫做加法原理。下面介绍一个链式法则
,这个也叫做加法原理。下面介绍一个链式法则
![]() 。
。
2.2.2.3 条件概率
2.2.3 贝叶斯理论
贝叶斯理论综合运用了加法和乘法的原理。具体如下:
2.2.3.1 例子:医疗诊断
这里讲了一个关于诊断乳腺癌的例子,假设有一个仪器,如果你有乳腺癌,那么你被诊断出来有乳腺癌的概率是0.8,即![]() 。这里事件x=1表示机器诊断出来你有乳腺癌,y=1表示事件你有乳腺癌。那么你如果被诊断出来有乳腺癌,你是否就认为你有80%的可能性患了乳腺癌呢。其实并不是,考虑p(y=1)=0.004,也就是一个人患乳腺癌的概率是0.004。我们假设如果你没有乳腺癌,那么机器判断你有的概率为0.1,即
。这里事件x=1表示机器诊断出来你有乳腺癌,y=1表示事件你有乳腺癌。那么你如果被诊断出来有乳腺癌,你是否就认为你有80%的可能性患了乳腺癌呢。其实并不是,考虑p(y=1)=0.004,也就是一个人患乳腺癌的概率是0.004。我们假设如果你没有乳腺癌,那么机器判断你有的概率为0.1,即![]() 。利用贝叶斯理论
。利用贝叶斯理论
那么可以看到,机器检测出你有乳腺癌,而实际上你有的概率只有0.031,所以这跟直觉上是不是相差很大呢。
2.2.3.2 例子:生成分类器
生成分类器利用公式
去进行分类,为什么称为生成分类器,因为它可以利用类条件概率![]() 和类先验
和类先验![]() 去生成数据。书后面会详细的讲这个,以及生成模型和判别模型的区别和优缺点。
去生成数据。书后面会详细的讲这个,以及生成模型和判别模型的区别和优缺点。
2.2.4 独立和条件独立
如果变量X和Y是独立的,这里就是指无条件独立,那么![]() 。这个比较好理解,就是两个事情风马牛不相及,扯不上关系。
。这个比较好理解,就是两个事情风马牛不相及,扯不上关系。
条件独立就是![]() 。公式很容易看懂,后面概率图模型中也会有很好的解释。不过一开始接触这个,我一直就理解不了,不知道怎么与实际对应起来。现在我就以自己的理解讲一下书上的例子。假设X是明天下雨,Y是今天地是湿的,Z是今天下雨。那么我说Y和X是关于Z独立的。为什么这么说,首先明天下雨跟今天地是湿的有关系,所以不独立,但是为什么有关系,因为地是湿的,所以很有可能今天下雨了,那么明天有可能会下雨的概率很大。但是我已经知道今天下雨了,所以我再去推断明天下不下雨,其实我完全就不需要知道地是否是湿的,所以就是独立的。这是我的个人理解,仅供参考。所以这里Y是通过Z影响X,我们通过Y去推断Z再去推断X,如果Z都知道了,那么你的Y就影响不到X了。
。公式很容易看懂,后面概率图模型中也会有很好的解释。不过一开始接触这个,我一直就理解不了,不知道怎么与实际对应起来。现在我就以自己的理解讲一下书上的例子。假设X是明天下雨,Y是今天地是湿的,Z是今天下雨。那么我说Y和X是关于Z独立的。为什么这么说,首先明天下雨跟今天地是湿的有关系,所以不独立,但是为什么有关系,因为地是湿的,所以很有可能今天下雨了,那么明天有可能会下雨的概率很大。但是我已经知道今天下雨了,所以我再去推断明天下不下雨,其实我完全就不需要知道地是否是湿的,所以就是独立的。这是我的个人理解,仅供参考。所以这里Y是通过Z影响X,我们通过Y去推断Z再去推断X,如果Z都知道了,那么你的Y就影响不到X了。
这里有个定理,如果X,Y关于Z是条件独立的,那么就存在两个函数g和h使得![]() ,这对于所有x,y,z都成立。
,这对于所有x,y,z都成立。
2.2.5 连续随机变量
这个就不详细说了,连续随机变量的概率密度函数就是pdf,概率密度函数的关于负无穷到x的积分就是累积分布函数cdf。
2.2.6 分位数
分位数有上侧![]() 分位数,双侧
分位数,双侧![]() 分位数,具体就不写了,可以参考概率论的书。
分位数,具体就不写了,可以参考概率论的书。
2.2.7 均值和方差
均值就是![]() ,积分域还有求和域就是x所能取到的所有的值。方差的定义和计算
,积分域还有求和域就是x所能取到的所有的值。方差的定义和计算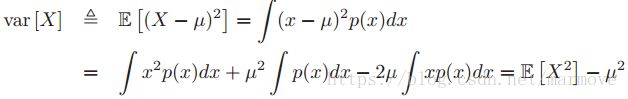 根据公式可以看到方差就是二阶矩减去均值的平方。标准差就是方差开根号。
根据公式可以看到方差就是二阶矩减去均值的平方。标准差就是方差开根号。
2.3 一些常见的离散分布
2.3.1 二项分布和伯努利分布
假设投一枚硬币n次,那么正面朝上的次数![]() 就是服从二项分布。假设每一次投正面朝上的概率为
就是服从二项分布。假设每一次投正面朝上的概率为![]() 。
。![]()
该分布的均值为![]() ,方差为
,方差为![]() 。这个利用定义很好算。伯努利分布就是二项分布n=1的特殊情况。可以写成两种形式
。这个利用定义很好算。伯努利分布就是二项分布n=1的特殊情况。可以写成两种形式
2.3.2 多项式分布和多元分布
多项式分布(multinomial distribution)于二项分布的区别就是,二项分布是扔硬币,多项式分布是掷色子,所以多项式分布就是有K面,每一面的概率就是![]() ,其中这K个值的和为1。那么投掷n次后,每一面出现的次数
,其中这K个值的和为1。那么投掷n次后,每一面出现的次数![]() (这K个数求和为n)称之为多项式分布。多项式分布的pmf是
(这K个数求和为n)称之为多项式分布。多项式分布的pmf是
多元分布(multinoulli distribution)就是多项式分布n等于1的情况。分布是 也可以表示成
也可以表示成![]() 。
。
2.3.3 泊松分布
2.3.4 经验分布
给定一个数据集,![]() ,我们给出了基于此集合的关于集合A的概率分布
,我们给出了基于此集合的关于集合A的概率分布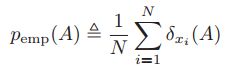 ,这称之为经验分布,或者叫经验测量。其中
,这称之为经验分布,或者叫经验测量。其中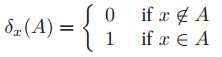 称之为Dirac measure。对于该概率分布,我们可以加权重,如果集合A就是一个值。那么概率分布写作
称之为Dirac measure。对于该概率分布,我们可以加权重,如果集合A就是一个值。那么概率分布写作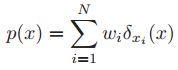 其中
其中![]() 并且
并且![]() 。
。
2.4 一些常见的连续分布
2.4.1 高斯分布
高斯分布可以说是最常见的一种分布了。高斯分布的pdf
其中,![]() 是均值,
是均值,![]() 是方差。
是方差。![]() 是标准高斯分布是,有时候我们经常说到高斯分布的精度参数,精度参数就是方差的倒数,
是标准高斯分布是,有时候我们经常说到高斯分布的精度参数,精度参数就是方差的倒数,![]() 。关于cdf我就不多说了,高斯分布的cdf是没有闭式表达式的,但是一般软件都会自带函数。
。关于cdf我就不多说了,高斯分布的cdf是没有闭式表达式的,但是一般软件都会自带函数。
为什么高斯分布在统计中是最广泛使用的分布呢。主要有三点,一是高斯分布所需要的两个参数,均值和方差和刻画分布特性的最好的东西。二就是中心极限定理,很多独立的随机变量的和可以用高斯分布来近似,所以我们用高斯分布来近似噪声是一个很好的选择。三就是高斯分布是均值和方差已知的情况下的最大熵分布。四就是高斯分布的数学形式简单,在计算上比较的方便。
2.4.2 退化pdf
当![]() 的时候,
的时候,![]() ,
,![]() 我们可以称之为冲激函数(Dirac delta function),定义为
我们可以称之为冲激函数(Dirac delta function),定义为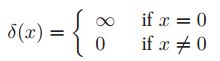 ,并且有
,并且有 ,冲激函数有个很好的性质就是筛选性质,
,冲激函数有个很好的性质就是筛选性质,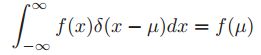
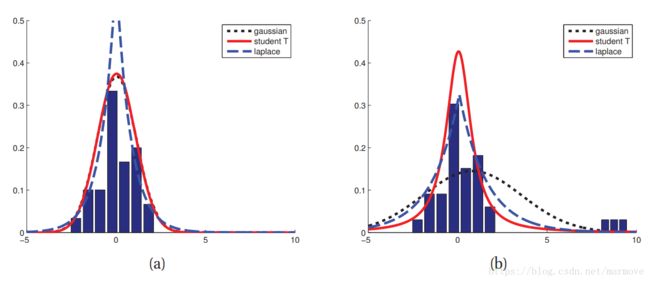
高斯分布存在一个问题,对于异常点,高斯分布很敏感如下图所示
高斯是黑色的虚线,第一幅图基本上与红线重合,二第二幅图就因为数据多了几个噪声点,高斯分布的形状就发生了巨大的改变。二红色的线跟之前基本上差不太多,那红色的是什么呢,是学生分布(student t distribution),这个分布具有更好的鲁棒性。学生分布的pdf
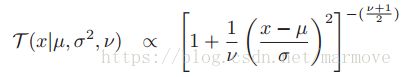 ,这个分布明显也是关于
,这个分布明显也是关于![]() 对称的,所以均值还有众数为
对称的,所以均值还有众数为![]() ,方差为
,方差为![]() ,这里
,这里![]() 是一个叫做自由度的参数。这里我们在算均值的时候,自由度
是一个叫做自由度的参数。这里我们在算均值的时候,自由度![]() ,在等于1的时候,利用均值的定义积分是积不出来的,在算方差是,同样
,在等于1的时候,利用均值的定义积分是积不出来的,在算方差是,同样![]() 。随着这个自由度
。随着这个自由度![]() 越来越大,当
越来越大,当![]() 时,这时候,学生分布就接近高斯分布,失去了它的良好的鲁棒性。当
时,这时候,学生分布就接近高斯分布,失去了它的良好的鲁棒性。当![]() 时,称之为柯西分布,这是一个重尾分布(heavy tail)。重尾分布如图
时,称之为柯西分布,这是一个重尾分布(heavy tail)。重尾分布如图
。小部分的数据占了大量的概率,后面大部分的数据概率比重很小。
2.4.3 拉普拉斯分布
这个分布也是重尾分布。![]() 代表位置信息,b代表尺度信息,b>0。该分布的均值为
代表位置信息,b代表尺度信息,b>0。该分布的均值为![]() ,众数为
,众数为![]() ,方差为
,方差为![]() 。
。
2.4.4 gamma分布
gamma分布的随机变量是大于0的,有两个参数,a>0表征形状,b>0表征速率。其概率密度函数具有如下形式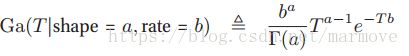
其中![]() 是gamma函数,定义为
是gamma函数,定义为 ,对于该分布,均值为a/b,众数为(a-1)/b,方差为a/(b^2)。
,对于该分布,均值为a/b,众数为(a-1)/b,方差为a/(b^2)。
gamma分布是一个非常灵活的分布,当a=1的时候,gamma分布又称作指数分布(exponential distribution)。当a=2的时候,gamma分布又称作埃尔朗分布(erlang distribution)。卡方分布(chi-squared distribution)定义为![]() ,该分布可以堪称若干个独立的标准高斯分布的求和。
,该分布可以堪称若干个独立的标准高斯分布的求和。
如果![]() ,那么
,那么![]() ,IG称为inverse gamma分布,其pdf定义为
,IG称为inverse gamma分布,其pdf定义为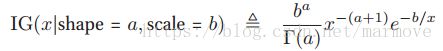 ,其具有如下性质
,其具有如下性质 ,均值仅仅在a>1时存在,方差也仅仅在a>2的时候存在。
,均值仅仅在a>1时存在,方差也仅仅在a>2的时候存在。
2.4.5 beta分布
beta分布是定义在[0,1]之间的,其概率密度函数定义如下:
2.4.6 帕累托分布
帕累托分布(pareto distribution)是用来表示一些重尾分布的。比如说单词,the,of这些单词占了太大的比重,或者说财富的分配,大量的钱集中在少数的富人的手中,这些都是典型的重尾分布。其定义如下
![]() 。这个分布很明显看出
。这个分布很明显看出![]() ,当
,当![]() ,这个分布接近于
,这个分布接近于![]() 。在log尺度下,这个分布呈现线性的性质。
。在log尺度下,这个分布呈现线性的性质。![]() a和c是常数。该分布具有如下的性质:
a和c是常数。该分布具有如下的性质:
2.5 联合概率分布
之前讲的都是单变量的概率分布,在这个章节中,我们主要介绍多变量的概率分布,这也是我们本书主要关注的。
2.5.1 协方差和相关
对于单变量,协方差定义为![]() 。对于多变量的分布,协方差矩阵(covariance matrix)定义如下
。对于多变量的分布,协方差矩阵(covariance matrix)定义如下
两个单变量变量的相关系数定义如下: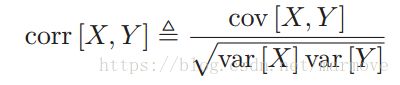 。对于多变量写成矩阵的形式,相关矩阵定义为:
。对于多变量写成矩阵的形式,相关矩阵定义为:
这里相关系数![]() ,并且,当X与Y之间存在线性关系时,等号才能取到。具体证明如下图:
,并且,当X与Y之间存在线性关系时,等号才能取到。具体证明如下图:
。
两个变量独立,那么![]() ,如果两个变量是独立的,那么则意味着它们不相关,但是两个变量是不相关的,并不意味着这两个变量是独立的。对于二维的高斯分布来说,不相关与独立是等价的。
,如果两个变量是独立的,那么则意味着它们不相关,但是两个变量是不相关的,并不意味着这两个变量是独立的。对于二维的高斯分布来说,不相关与独立是等价的。
2.5.2 多元高斯分布
多元高斯分布或者也叫做多元正态分布,是连续随机变量中,最常见的联合概率分布。多元高斯分布的概率密度函数如下:
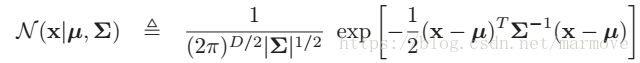 ,
,![]() ,并且
,并且![]() ,是一个
,是一个![]() 的矩阵。有时候我们也用精度矩阵来刻画,
的矩阵。有时候我们也用精度矩阵来刻画,![]() 。协方差矩阵是高斯分布比较复杂的部分,因为其有D(D+1)/2个参数,所以有时候我们往往假设其是对角阵,这样只有D个参数。
。协方差矩阵是高斯分布比较复杂的部分,因为其有D(D+1)/2个参数,所以有时候我们往往假设其是对角阵,这样只有D个参数。
2.5.3 多元学生t分布
多元学生分布的pdf如下:
2.5.4 狄利克雷分布(Dirichletdistribution)
beta分布的多元分布就是狄利克雷分布,其定义如下:
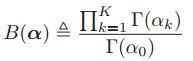 ,
,![]() ,
,![]() 。对于狄里克雷分布来说,
。对于狄里克雷分布来说,![]() 是控制着峰的尖锐程度,越大那么就越尖,越小就越平坦。
是控制着峰的尖锐程度,越大那么就越尖,越小就越平坦。![]() 则是控制峰的位置。该分布的性质如下:
则是控制峰的位置。该分布的性质如下:
2.6 随机变量的变换
如果![]() 是一个随机变量,并且y=f(x),那么y的分布是什么样子的呢?
是一个随机变量,并且y=f(x),那么y的分布是什么样子的呢?
2.6.1 线性变换
如果f()是一个线性方程,那么![]() 。对于这种情况我们能够比较好的计算均值和方差。其中
。对于这种情况我们能够比较好的计算均值和方差。其中![]()
![]() ,
,![]() 。方差这里的证明直接利用公式(2.66)易得出:
。方差这里的证明直接利用公式(2.66)易得出:
![]() 。
。
2.6.2 一般化的变换
离散化的变量非常简单,直接数哪些x映射到了y,然后把相应的概率加起来就好了,即![]() 。
。
那么如果是连续的变量,那么我们可以从cdf入手,![]() ,求个导就得到pdf。如果f(x)是单调赠的,那么
,求个导就得到pdf。如果f(x)是单调赠的,那么![]() ,进一步可以得到:
,进一步可以得到:
2.6.2.1 多变量到多变量的变换
假设f函数是![]() ,雅克比矩阵(Jacobian matrix)写作:
,雅克比矩阵(Jacobian matrix)写作:
2.6.3 中心极限定理
假设有N个独立同分布的(independent and identically distributed,iid)随机变量(random variables,RV),它们的均值为![]() ,方差为
,方差为![]() 。令
。令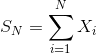 ,是前面N个随机变量的和。随着N的不断增大,那么
,是前面N个随机变量的和。随着N的不断增大,那么![]() 服从均值为
服从均值为![]() ,方差为
,方差为![]() 的高斯分布。
的高斯分布。
2.7 蒙特卡罗(Monte Carlo)近似
在实际情况中,特别是在变量通过函数变换后,其概率密度函数是比较难以算得闭式表达式的。所以说我们先进行采样,生成S个样本![]() ,生成样本的方法有很多(通过cdf,MCMC等),然后我们通过
,生成样本的方法有很多(通过cdf,MCMC等),然后我们通过![]() 去近似的估计f(X)、这就是蒙特卡洛近似。比如说我们进行均值的估计,那么
去近似的估计f(X)、这就是蒙特卡洛近似。比如说我们进行均值的估计,那么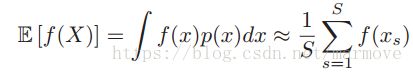 。通过改变f(X)的形式。蒙特卡洛可以近似很多我们感兴趣的量:这里我没太懂下面的f(X)具体什么形式,第一个可能f(X) = X,第二个也好弄,后面两个好像不太找得到。但是总的来说就是利用采样的数据去估计原来真实分布的一些量。
。通过改变f(X)的形式。蒙特卡洛可以近似很多我们感兴趣的量:这里我没太懂下面的f(X)具体什么形式,第一个可能f(X) = X,第二个也好弄,后面两个好像不太找得到。但是总的来说就是利用采样的数据去估计原来真实分布的一些量。
2.7.1 例子:变量变换,MC方法
这里就是上面说过了,在原始的概率分布上采样,然后通过函数f(x)之后,得到变换过的变量y的的采样,这样经验的去估计y的概率分布。
2.7.2 例子:通过蒙特卡罗积分去估计
首先给出一幅图:
然后我们给出下面的式子: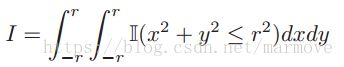 这其实就是圆心为(0,0),半径为r的圆的面积。那么
这其实就是圆心为(0,0),半径为r的圆的面积。那么![]() ,那么如果我们用蒙特卡罗的方法怎么去估计这个
,那么如果我们用蒙特卡罗的方法怎么去估计这个![]() ,就是随机的取点(x,y),x服从[-2,2]的均匀分布,y服从[-2,2]的均匀分布,那么所有满足
,就是随机的取点(x,y),x服从[-2,2]的均匀分布,y服从[-2,2]的均匀分布,那么所有满足![]() 的点除以所有的点就是
的点除以所有的点就是![]() 的估计值,当我们采样的点越来越多,
的估计值,当我们采样的点越来越多,![]() 估的就越准确。书上的公式就是这个意思,积分式就相当于采样了所有的点,后面的约等式就是S采样点去进行近似。
估的就越准确。书上的公式就是这个意思,积分式就相当于采样了所有的点,后面的约等式就是S采样点去进行近似。
2.7.3 蒙特卡罗近似的准确度
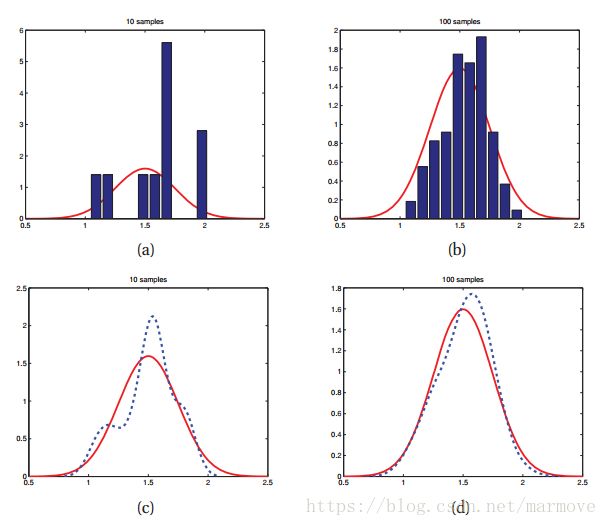
在蒙特卡洛近似的时候,你的样本越多,那么近似的效果就越好。书上给了一个例子:
左边是10次采样,右边100次,红色的实线是真实的高斯分布,均值1.5,方差0.25。蓝色的虚线是直方图采样的平滑后的样子,很明显,100次采样的两条线更加的接近。
对于X的均值是![]() ,方差是
,方差是![]() ,那么
,那么![]() ,根据中心极限定理,其必定是服从均值为
,根据中心极限定理,其必定是服从均值为![]() ,方差为
,方差为![]() 的高斯分布,所以有
的高斯分布,所以有![]() 。由于实际上真实的X的均值在现实中是不知道的。所以在进行方差估计时,用
。由于实际上真实的X的均值在现实中是不知道的。所以在进行方差估计时,用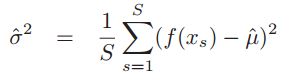 。
。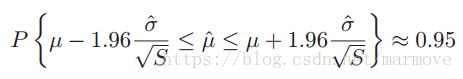 这个式子中
这个式子中![]() 理论上应该是用真实值,这其实就是由于
理论上应该是用真实值,这其实就是由于![]() 服从高斯分布得到的,但是真实值不知道,用估计值来替代。个人感觉这个式子的准确性就有待考证?但是总之随着S的增大,真实的均值和估计的均值会完全一样。这一点是可以肯定的。
服从高斯分布得到的,但是真实值不知道,用估计值来替代。个人感觉这个式子的准确性就有待考证?但是总之随着S的增大,真实的均值和估计的均值会完全一样。这一点是可以肯定的。
2.8 信息论
信息论考虑的是对于数据用更加紧凑的方式去表示(比如数据的压缩或者是源编码)以及在数据的存储或者传递时对于一些错误会有很好的鲁棒性。
2.8.1 熵
书上这里没有讲,但是我觉得还是可以提一下,首先引入自信息的概念。对于一个随机变量X,它的概率分布是p。自信息的定义为![]() (这里说一下,不同的底单位不一样,我们这里用比特,其余的网上可以搜到),自信息就是该事件发生所带来的信息量,容易看出,概率越低,发生带来的信息量越大,这也很好理解。那么什么是熵,熵就是随机变量X自信息的期望:
(这里说一下,不同的底单位不一样,我们这里用比特,其余的网上可以搜到),自信息就是该事件发生所带来的信息量,容易看出,概率越低,发生带来的信息量越大,这也很好理解。那么什么是熵,熵就是随机变量X自信息的期望:
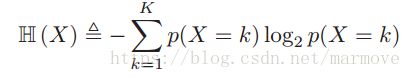 这个是假设X是离散的,连续的用积分表示就好。那么熵最大的时候就是均匀分布,熵最小的时候就是delta函数(离散的话就是有一个事件发生概率为1,其余都为0)。书上的例子就是离散概率分布K=2的例子。
这个是假设X是离散的,连续的用积分表示就好。那么熵最大的时候就是均匀分布,熵最小的时候就是delta函数(离散的话就是有一个事件发生概率为1,其余都为0)。书上的例子就是离散概率分布K=2的例子。
2.8.2 KL距离
下面我们要介绍一个东西叫KL距离也可以叫做相对熵。定义如下
 ,这里要注意,KL距离与传统意义上的距离不一样,它并不具有交换性。
,这里要注意,KL距离与传统意义上的距离不一样,它并不具有交换性。
这里我们可以把KL距离改写一下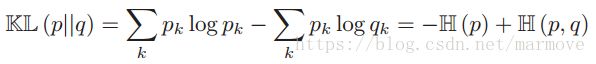 ,这里
,这里 叫做交叉熵。交叉熵是什么意思呢,就是说你真是的信号是从p分布中抽取的,而我用模型q去定义我们的编码本,那么平均需要用多少的比特,而KL距离就是当你用q去对p进行编码的时候比用p对p进行编码多用的比特数目。从这点来理解KL距离大于等于0就不难了,当然我们用真实的去编码肯定需要的比特最少,用其他的q去编码肯定会多,所以KL大于等于0。
叫做交叉熵。交叉熵是什么意思呢,就是说你真是的信号是从p分布中抽取的,而我用模型q去定义我们的编码本,那么平均需要用多少的比特,而KL距离就是当你用q去对p进行编码的时候比用p对p进行编码多用的比特数目。从这点来理解KL距离大于等于0就不难了,当然我们用真实的去编码肯定需要的比特最少,用其他的q去编码肯定会多,所以KL大于等于0。
书上定理2.8.1:KL(p||q)大于等于0,当且仅当p=q的时候取到等号。为了证明这个,我们需要用到 Jensen's 不等式,具体定义如下:
下面回到定理的证明,我解释一下书上的证明:
首先A是指概率分布p的x支撑的集合,就是x所有可能取到的值构成的集合,![]() 是对于概率分布q而言的x支撑的集合,
是对于概率分布q而言的x支撑的集合,![]() 。第一个不等式就是利用的jensen不等式,其中p(x)就是
。第一个不等式就是利用的jensen不等式,其中p(x)就是![]() ,而log就是f。第二个不等式就是说对于q来讲肯定是自己的支撑集
,而log就是f。第二个不等式就是说对于q来讲肯定是自己的支撑集![]() 进行求和更大。针对第一个不等式成立,要求p与q之间成比例关系,第二个不等式成立则要求
进行求和更大。针对第一个不等式成立,要求p与q之间成比例关系,第二个不等式成立则要求![]() ,这样的话也就是说p和q要是完全一样的,KL距离才会为0。
,这样的话也就是说p和q要是完全一样的,KL距离才会为0。
根据这个结论,我们可以得到一个很重要的结果,那就是离散随机变量的最大熵分布是均匀分布。这个很好证明:
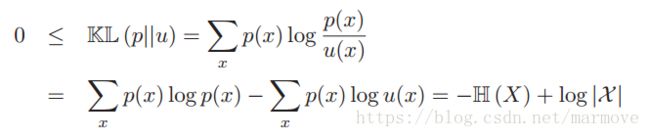 这里u是均匀分布,p是任何一个分布。由KL距离大于等于0很容易得到。这个告诉我们当我们不知道什么分布更合适,没有任何倾向的时候,那么就采用均匀分布,这叫理由不充分原则(principle of insufcient reason)。
这里u是均匀分布,p是任何一个分布。由KL距离大于等于0很容易得到。这个告诉我们当我们不知道什么分布更合适,没有任何倾向的时候,那么就采用均匀分布,这叫理由不充分原则(principle of insufcient reason)。
2.8.3 互信息
给定两个随机变量X和Y,互信息考虑的是他们的联合概率分布p(X,Y)和p(X)p(Y)之间的距离。所以说互信息的定义如下:
对于互信息我们还有其他的表达方式,利用条件信息和自信息表示: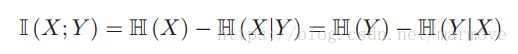 ,其中
,其中![]() 就是条件熵,定义为:
就是条件熵,定义为:![]() ,还有一个定义叫做点互信息(pointwise mutual information):
,还有一个定义叫做点互信息(pointwise mutual information):
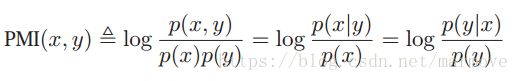 ,这里是针对两个事件。这里我仅仅引入这些概念,由于我并不能从宏观上把握,但是后面的学习肯定会慢慢更深的了解。
,这里是针对两个事件。这里我仅仅引入这些概念,由于我并不能从宏观上把握,但是后面的学习肯定会慢慢更深的了解。
2.8.3.1 连续随机变量的互信息*
对于连续变量怎么计算互信息,一种比较常见的方法就是离散化,将连续量划分成不同的区间,然后每一个区间作为一个离散值,实现离散化。但是呢怎么划分就是会比较的复杂,一种就是直接对离散的量进行互信息的计算,另一种就是尝试许多不同的划分的方法,取互信息最大的那个。这个被称作最大信息系数(maximal information coefficient),定义如下: