变分自编码器ELBO的求解---随机梯度变分估计(SGVB)
在变分自编码(VAE)一文中我们已经求解了VAE的ELBO,这里再进一步分析求解ELBO的方法,也就是SGVB估计。
两种形式的ELBO
变分自编码器的ELBO其实有两种形式:
第一种是:
E L B O = E q φ ( z ∣ x ) [ l o g p θ ( x , z ) q φ ( z ∣ x ) ] = E q φ ( z ∣ x ) [ l o g p θ ( z ) p θ ( x ∣ z ) q φ ( z ∣ x ) ] = E q φ ( z ∣ x ) [ l o g p θ ( x ∣ z ) ] − K L [ q φ ( z ∣ x ) ∣ ∣ p θ ( z ) ] (1) \tag{1} \begin{aligned} ELBO = & E_{q_{\varphi}(z|x)}[log{p_{\theta}(x, z) \over q_{\varphi}(z|x) }] \\ = & E_{q_{\varphi}(z|x)}[log{p_{\theta}(z)p_{\theta}(x|z) \over q_{\varphi}(z|x)}] \\ = & E_{q_{\varphi}(z|x)}[logp_{\theta}(x|z)] - KL[q_{\varphi}(z|x)||p_{\theta}(z)] \end{aligned} ELBO===Eqφ(z∣x)[logqφ(z∣x)pθ(x,z)]Eqφ(z∣x)[logqφ(z∣x)pθ(z)pθ(x∣z)]Eqφ(z∣x)[logpθ(x∣z)]−KL[qφ(z∣x)∣∣pθ(z)](1)
第二种是:
E L B O = E q φ ( z ∣ x ) [ l o g p θ ( x , z ) q φ ( z ∣ x ) ] = E q φ ( z ∣ x ) [ l o g p θ ( x , z ) q φ ( z ∣ x ) ] = E q φ ( z ∣ x ) [ l o g p θ ( x , z ) ] + H q φ ( z ∣ x ) ( z ) 其 中 , H q φ ( z ∣ x ) ( z ) = ∫ z − q φ ( z ∣ x ) l o g q φ ( z ∣ x ) d z (2) \tag{2} \begin{aligned} ELBO = & E_{q_{\varphi}(z|x)}[log{p_{\theta}(x, z) \over q_{\varphi}(z|x) }] \\ = & E_{q_{\varphi}(z|x)}[log{p_{\theta}(x,z) \over q_{\varphi}(z|x)}] \\ = & E_{q_{\varphi}(z|x)}[logp_{\theta}(x,z)] + H_{q_{\varphi}(z|x)}(z) \\ 其中,H_{q_{\varphi}(z|x)}(z) = & \int_{z}-q_{\varphi}(z|x)logq_{\varphi}(z|x)dz \end{aligned} ELBO===其中,Hqφ(z∣x)(z)=Eqφ(z∣x)[logqφ(z∣x)pθ(x,z)]Eqφ(z∣x)[logqφ(z∣x)pθ(x,z)]Eqφ(z∣x)[logpθ(x,z)]+Hqφ(z∣x)(z)∫z−qφ(z∣x)logqφ(z∣x)dz(2)
SGVB估计求解ELBO
先求解(1)式,先考虑(1)式中的第一项,第一项式期望的形式,期望可以通过蒙特卡洛估计来求解,不懂的可以看这篇博客蒙特卡洛估计。
从 q φ ( z ∣ x ) q_{\varphi}(z|x) qφ(z∣x)中依据z的概率分布采样L个点,即
E q φ ( z ∣ x ) [ l o g p θ ( x ∣ z ) ] ≈ 1 L ∑ l = 1 L l o g p θ ( x ∣ z ( l ) ) (3) \tag{3}E_{q_{\varphi}(z|x)}[logp_{\theta}(x|z)] \approx {1 \over L}\sum_{l =1}^{L}logp_{\theta}(x|z^{(l)}) Eqφ(z∣x)[logpθ(x∣z)]≈L1l=1∑Llogpθ(x∣z(l))(3)
这样通过采样貌似可以,但是我们还要通过采样来反向梯度优化 φ \varphi φ,这样采样之后 E q φ ( z ∣ x ) [ l o g p θ ( x ∣ z ) ] E_{q_{\varphi}(z|x)}[logp_{\theta}(x|z)] Eqφ(z∣x)[logpθ(x∣z)]就与 φ \varphi φ无关了,因此这个操作是不可导的,就需要重参数化技巧来使采样操作可导。我们假设 z ( l ) = g φ ( x , ε ( l ) ) , ε ( l ) ∼ p ( ε ) z^{(l)} = g_{\varphi}(x, \varepsilon^{(l)}),\varepsilon^{(l)} \sim p(\varepsilon) z(l)=gφ(x,ε(l)),ε(l)∼p(ε),其中 p ( ε ) 和 g φ p(\varepsilon)和g_{\varphi} p(ε)和gφ都是形式已知的。这样(3)式对 φ \varphi φ就可导了,因为 g φ g_{\varphi} gφ中含有参数 φ \varphi φ。
(3)式就变成了:
E q φ ( z ∣ x ) [ l o g p θ ( x ∣ z ) ] ≈ 1 L ∑ l = 1 L l o g p θ ( x ∣ g φ ( x , ε ( l ) ) ) ε ( l ) ∼ p ( ε ) (4) \tag{4} E_{q_{\varphi}(z|x)}[logp_{\theta}(x|z)] \approx {1 \over L}\sum_{l =1}^{L}logp_{\theta}(x|g_{\varphi}(x,\varepsilon^{(l)})) \\ \varepsilon^{(l)} \sim p(\varepsilon) Eqφ(z∣x)[logpθ(x∣z)]≈L1l=1∑Llogpθ(x∣gφ(x,ε(l)))ε(l)∼p(ε)(4)
(4)式就是用SGVB估计得到的。
所以(1)式可进一步写成
L ( φ , θ , x ) = 1 L ∑ l = 1 L l o g p θ ( x ∣ z ( l ) ) − K L ( q φ ( z ∣ x ) ∣ ∣ p θ ( z ) ) = 1 L ∑ l = 1 L l o g p θ ( x ∣ g φ ( x , ε ( l ) ) ) − K L ( q φ ( z ∣ x ) ∣ ∣ p θ ( z ) ) (5) \tag{5} \begin{aligned} L(\varphi,\theta,x) = & {1 \over L}\sum_{l =1}^{L}logp_{\theta}(x|z^{(l)}) - KL(q_{\varphi}(z|x)||p_{\theta}(z)) \\ = & {1 \over L}\sum_{l=1}^{L}logp_{\theta}(x|g_{\varphi}(x, \varepsilon^{(l)})) -KL(q_{\varphi}(z|x)||p_{\theta}(z)) \\ \end{aligned} L(φ,θ,x)==L1l=1∑Llogpθ(x∣z(l))−KL(qφ(z∣x)∣∣pθ(z))L1l=1∑Llogpθ(x∣gφ(x,ε(l)))−KL(qφ(z∣x)∣∣pθ(z))(5)
其中 ε ( l ) ∼ p ( ε ) \varepsilon^{(l)} \sim p(\varepsilon) ε(l)∼p(ε),
在实际计算时,我们假设 p θ ( z ) ∽ N ( z ; 0 , I ) , q φ ( z ∣ x ) ∽ N ( z ; μ , σ ) , z 的 维 度 是 J p_{\theta}(z)\backsim N(z;0,I),q_{\varphi}(z|x) \backsim N(z;\mu,\sigma),z的维度是J pθ(z)∽N(z;0,I),qφ(z∣x)∽N(z;μ,σ),z的维度是J,二者的KL散度可以得到解析形式:

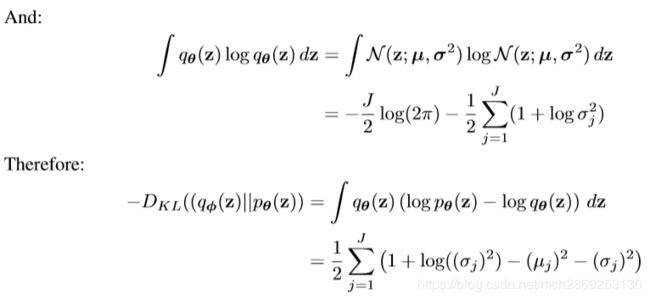
因此,最后(5)式就变成了:
L ( φ , θ , x ) = 1 L ∑ l = 1 L l o g p θ ( x ∣ g φ ( x , ε ( l ) ) ) + 1 2 ∑ j = 1 J ( 1 + l o g ( σ j 2 ) − μ j 2 − σ j 2 ) ) 其 中 ε ( l ) ∼ p ( ε ) (6) \tag{6} \begin{aligned} L(\varphi,\theta,x) = {1 \over L}\sum_{l=1}^{L}logp_{\theta}(x|g_{\varphi}(x, \varepsilon^{(l)})) +{1 \over 2} \sum_{j=1}^{J}(1+log(\sigma_{j}^{2})-\mu_{j}^{2}-\sigma_{j}^{2})) \\ 其中\varepsilon^{(l)} \sim p(\varepsilon) \end{aligned} L(φ,θ,x)=L1l=1∑Llogpθ(x∣gφ(x,ε(l)))+21j=1∑J(1+log(σj2)−μj2−σj2))其中ε(l)∼p(ε)(6)